
∀人∃HEYA入門と自作の解説+α
はじめまして。もやと申します。普段はBeginners Puzzle Contestの作問に関わったり、ニコリに問題を投稿したりしている者です。
この記事はペンシルパズルI Advent Calendar 2021の8日目の記事となっています。
0.はじめに
タイトルにある「∀人∃HEYA」とは変種のへやわけの一種で、へやわけのルールに「すべての部屋には、黒マスが点対称に入る」というルールが追加されたものです。
その∀人∃HEYAが割と好きなのですが、∀人∃HEYAについて書かれたネット記事がほとんどなさそうだったので、自分で書いてみることにしました。(と書くつもりだったのですが、調べながら記事を書いていたらいくつかあることがわかりました。)
この記事では、前半は∀人∃HEYA初心者〜中級者向けに例題の解説と考え方の紹介を行い、後半では自作の(やや)難しい問題の解説をしたり、不定形の世界を覗き見たり、その他∀人∃HEYAに関することをだらだら書いたりしています。
注意:へやわけについてはある程度知っていることを前提としています。(ヤバい手筋の知識は不要で(自分も知らないです)、パズルスクエアのおてごろやニコリのたいへんが解けるかなくらいで大丈夫です。)へやわけってなんぞや?という方は、ペンシルパズルwikiやペンシルパズル百科をご覧ください。
∀人∃HEYAについての記事
トクナキラさん ∀人∃HEYA(ぜんべや)の解き方
∀人∃HEYAに触れている、へやわけについての記事
半袖さん アド街っぽくパズルを語る ~へやわけ編~ の後編
謎垢さん へやわけ考え方・手筋集
→オマケとして∀人∃HEYAの手筋が紹介されています。
名前の由来
ホームさんが以前に言及されていました。(原作者のにゃんこばずうかさんのコメントのようです。にゃんこばずうかさんのブログは閉鎖してしまったようです。)ぜんべやと呼ぶ人が多い印象で、この記事でも以降はぜんべやと呼ぶことにします。
思いついたパズルのタイトルは表題の通り「∀人∃HEYA」。「∀」とか「∃」とかは数学記号で,それぞれ「すべての~に対し」「ある~が存在して」というくらいの意味。だからして「すべてのひとにはへやがある」とでも読みますかね。略して「ぜんべや」。
— ホーム (@homerestaurant3) September 6, 2019
1.入門編
ルールは簡単で、へやわけのルールに「すべての部屋には、黒マスが点対称に入ります。」とルールが追加されたものです。
(再掲:へやわけについてはペンシルパズルwikiが詳しいです。ペンシルパズル百科もご覧ください。)
1.盤面のいくつかのマスを黒くぬりましょう。
2.太線で区切られた四角(部屋と呼びます)に入っている数字は、その部屋に入る黒マスの数を表しています。数字の入っていない部屋には、いくつ黒マスが入るかわかりません。
3.白マスを、タテまたはヨコにまっすぐに3つ以上の部屋にわたって続けさせてはいけません。
4.黒マスをタテヨコに連続させたり、黒マスで盤面を分断したりしてはいけません。
5.すべての部屋には、黒マスが点対称に入ります。
(Puzzle Square JPより)
ぜんべや初見勢を想定して例題を置いておきますが、もっと解きたい方は以下のページを覗いてみるといいかもしれません。
最近はオンラインの問題集としてパズルスクエアが紹介されがちですが、ニコリ系は過去に作家の方が個人ブログで公開されていたりします。パズルスクエアよりもこの類のブログの方が初心者にはいいと思うので、いくつか勝手に紹介させていただきます。(問題があればご連絡ください。)
例題

ぱずぷれはこちら
20行下から解説が始まります。
解説

2つの2は、へやわけでよくある入り口ですね。

そこから白マスが数カ所決まりますが、そのマスの点対称の位置も白マスになります。

ここから新たに黒マスが決まります。再び点対称の位置に黒マスを置きましょう。


4の部屋の黒マスの位置が全て決まったので他のマスは白マスになり...
残りが三連禁・分断禁により決まります。

完成です。お疲れ様でした。
2.よく使う考え方
へやわけの手筋は上記のペンシルパズル百科から飛べる記事でまとめられているのでいいとして、ぜんべや特有の考え方がいくつかあります。
注意
・必ずしも初級手筋から上級手筋の順に並んでいるわけではありません。
・実用性重視なので、パズルスクエア等で出現頻度の低い手筋は省略しています。
・トクナキラさん・謎垢さんの記事と被っているところも多いですが、許してください。
(再掲:トクナキラさん ∀人∃HEYA(ぜんべや)の解き方/謎垢さん へやわけ考え方・手筋集)
考え方1:奇数×奇数の部屋の中央のマスは部屋の数字の偶奇で決まる
奇数なら中央のマスは黒、偶数なら中央のマスは白です。

すぐ決まる部屋の例

(点対称ルールなしでも決まる一列の部屋や5in3×3は省略しています。)
考え方2:対称位置のマスを同時に仮定
例1:奇数×偶数の部屋の中央2マスは必ず白

2×(2n-1)のへやは頻出です。覚えておきましょう。
2×3のへやが隣接して三連禁で黒マスが決まる展開はよく見ますね。
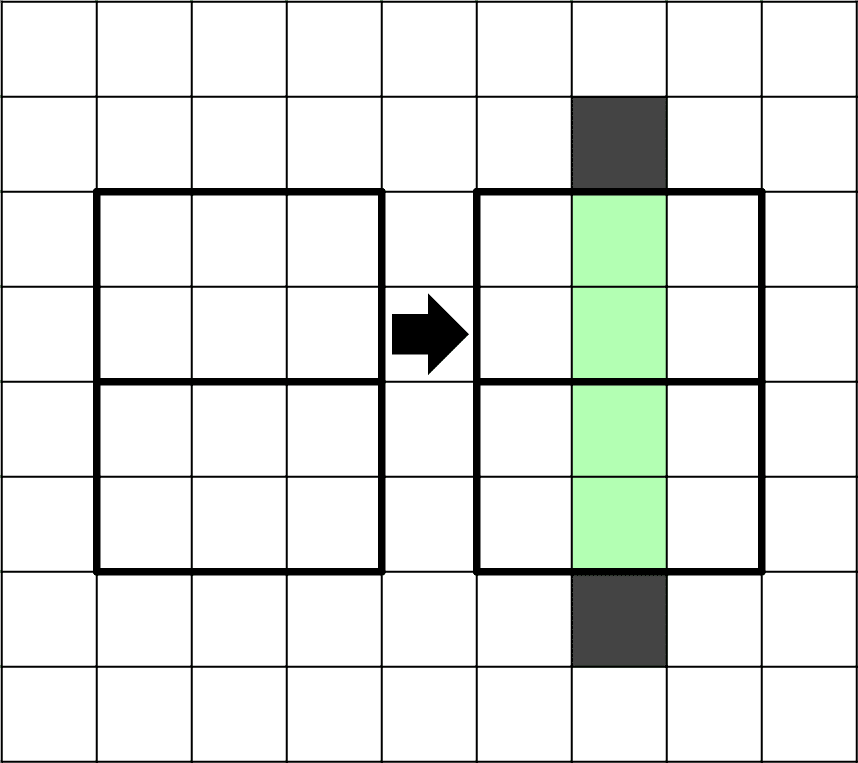
例2:分断禁

角の3もよく見るパターンです。2×2や3×3ではわざわざ「対称位置のマスを同時に仮定」するまでもないとは思いますが大部屋中に出てくることもあります。
その他の例

対称位置にあるマスのペアの白黒は一致するので、両方白か両方黒かのいずれかでハタンする場合は、もう一方になります。(一番下の例は、下が外壁とします)
考え方3:黒マスが入る列を考える

ある列に黒マスが入ることが決まると、その対称位置の列にも黒マスが1つ入ることが決まります。上の例はホワイトニングの例です。
上下の行で黒マスを1つずつ配置するので、2つの黒マスの位置が確定し、中央4マスが白に確定します。
個別のパターンを列挙しても実用性に欠けると思うので、普通の問題を解く上で知っておくべき手筋はこんなものでしょうか。
他にあればコメントやDM等で教えて下さい。
オマケ:黒マス最大値
へやわけよりも最大値が小さくなる部屋があります。
ある部屋に配置できる黒マスの最大値を青字で、配置する方法の例を青マスで示しています。確定するわけではないのでご注意ください。
1×nの部屋では、最大値はへやわけでもぜんべやでも変わりません。
壁沿いでない2×nの部屋は簡単で、2×偶数なら同じ、2×奇数なら奇数×偶数の部屋の中央2マスは必ず白であることから最大値が1小さくなります。

壁沿いの2×nの部屋では、2×3の長方形空間に黒マスが3つ入ると、その対称位置で分断が生じることも、へやわけより最大黒マス数が小さくなる原因となります。




もちろん、複数の部屋にまたがる場合は問題ありません。また、2×nの部屋でなければ点対称位置で分断されないので問題ありません。


5×5以下は以下のようになります。(3×3のみ一意に決まるので、黒と緑色にしています。)


5×5はへやわけの最大値が11ですが、その配置が点対称配置なのでぜんべやでも同じになります。
3.自作の解説
パズルスクエアに最近投稿したぜんべや4問の解説をします。
難易度はどれもたいへん〜アゼンくらいだと思います。
1問目

奇数×奇数の部屋で、中央の黒マスから決まるのが好きで作った問題でした。解けた方は類題の変種Aqreもどうぞ。(ぜんべやではありません)
20行下から解説が始まります。

ここまではいいでしょう。9の部屋の左半分での充填を考えると、4つの2×2エリアに2つずつ黒マスが入ることがわかります。


分断禁で決まりました。
左下の2×4の部屋は、上で紹介した「黒マスが入る列を考える」と「黒マスが入る列を考える」により、4つの黒マスが入ることがわかります。

初めと似たような形になりますが、壁沿いではないので同じ決まり方はしません。上図のAAかBBのいずれかが共に黒マスになると、分断が発生してしまいますが、Cを黒マスにすると、AAあるいはBBの組に黒マスを置かざるを得なくなってしまうので、Cは白マスになります。
あとは分断禁を気にしながら解けると思います。
2問目

コンセプトは見えない部屋同士の相互作用、ぜんべやの良さを活かしつつもぜんべやではあまり登場しないへやわけならではの考え方を入れ込むことができてかなりお気に入りの問題です。見た目も良い。
20行下から解説が始まります。

すぐ決まるのは1だけですが、実は見えない部屋が4つあります。

上図の青四角で囲った領域には3つの黒マスが入りますが、これは、白マスの隣に境界線が2本並んでいるときに、ABともに白になると三連禁に反するので、どちらかが黒になるためです。

これがわかれば8割解けたようなものです。壁沿いの2×3の部屋の隣は白マスになるへやわけの手筋から白マスが決まり、

こうなれば右上から解けていけると思います。

最後も見えない部屋が登場します。中央をいい感じに決めて完成です。
3問目

もともと正方形の大部屋が大好きで、このぜんべやを作ったあとに数字無しで作れないかなと試してみたらできてしまった問題です。これも気に入っています。
20行下から解説が始まります。
右下の角の部屋の黒マスの数は0か2になりますが、0になると三連禁を回避できないので、2になります。このことから下の画像まで決まると思います。

Aのペアは黒にすると分断してしまうので、白になります。

上から5行目と6行目の周りの三連禁回避のために青のうちどちらか、右から2列目の三連禁回避のために赤のうちどちらかが黒マスになります。点対称位置に黒マスが入ることから以下のようになり、分断禁で決まりますね。

ここからかなり進みます。

Bは分断禁から白、Cは三連禁から黒ですね。
Cが黒になると、Dが分断禁から白になります。
残りは三連禁に気をつけながら埋めましょう。
4問目

かなり難しいです。先に練習問題として次のへやわけを解くとよいかもしれません。(へやわけを作ってぱずすくに投稿してから、ぜんべやへの応用を思いつきました。)
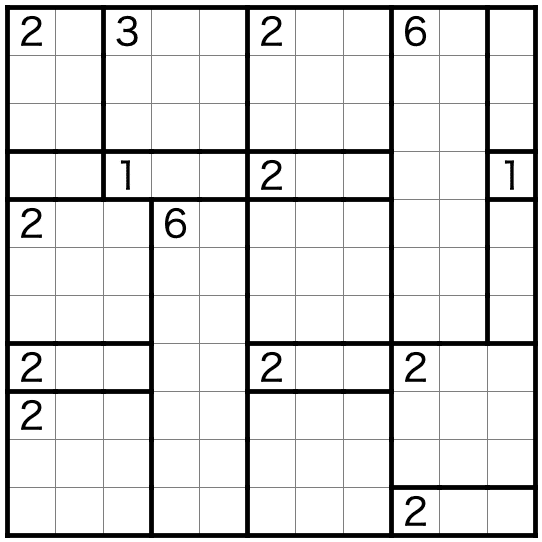
20行下から解説が始まります。
へやわけはそこまで難しくないので細かくは解説しませんが、この「1列のへやを横断して白マスがつながることはできない」という考え方が大切になります。
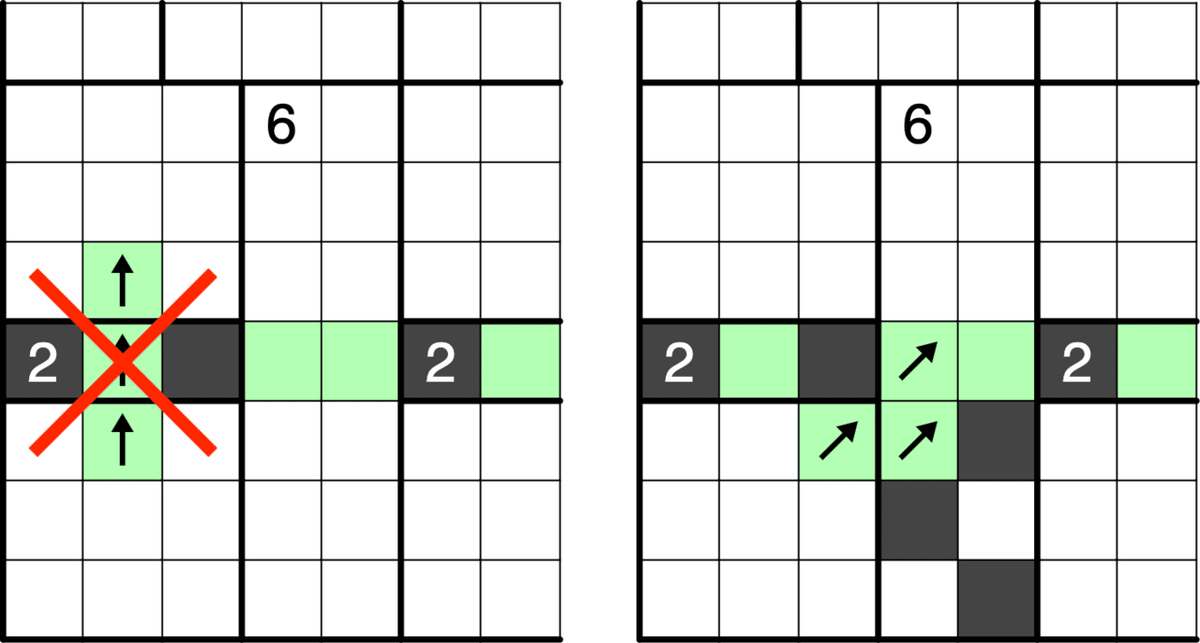
ここからぜんべやの解説になります。大きなテーマは練習問題のへやわけと同じですが、6in2×7の上下の形が点対称になるということが違っています。

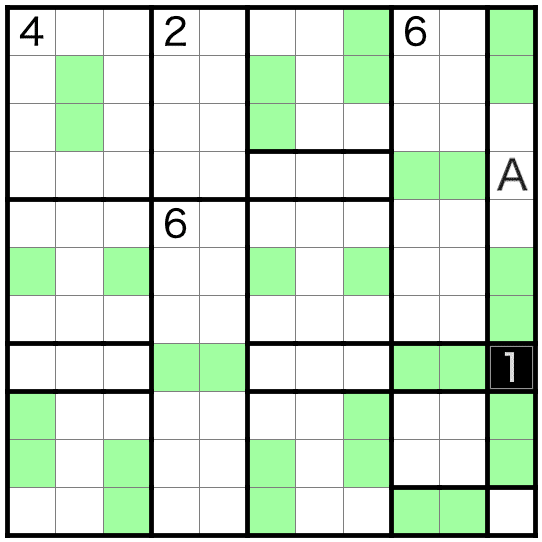
このことにより、上図のAを黒マスにすると、上下いずれかが閉じ込められてハタンしてしまうので、Aが白マスになり、三連禁から少し進みます。(想定していた入り口はここですが、わかりにくいですね。他の場所で仮定をしても、2枚下の画像までは割と楽に決まってしまうかもしれません。)
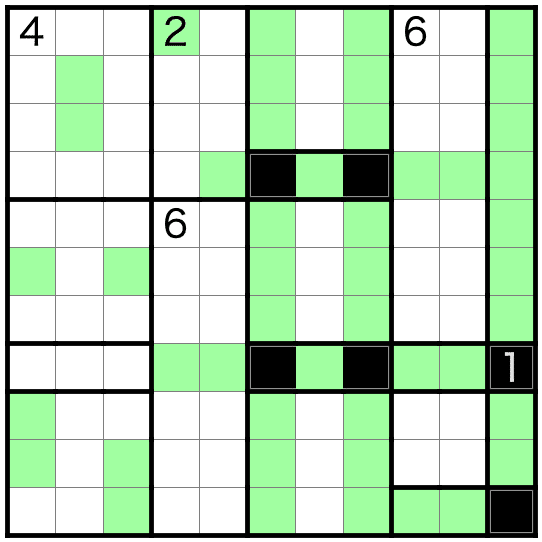
2のへやは、三連禁回避のために中央2行に黒マスが必要なので、上下2行は白マスになります。

ここがこの問題の肝です。入り口がわからず解説を読んでいる人も、ここでもう一度立ち止まって考えてみてもらえればと思います。
ごちゃごちゃしていてわかりにくいので最低限必要な部分だけ抽出すると、以下のようになります。
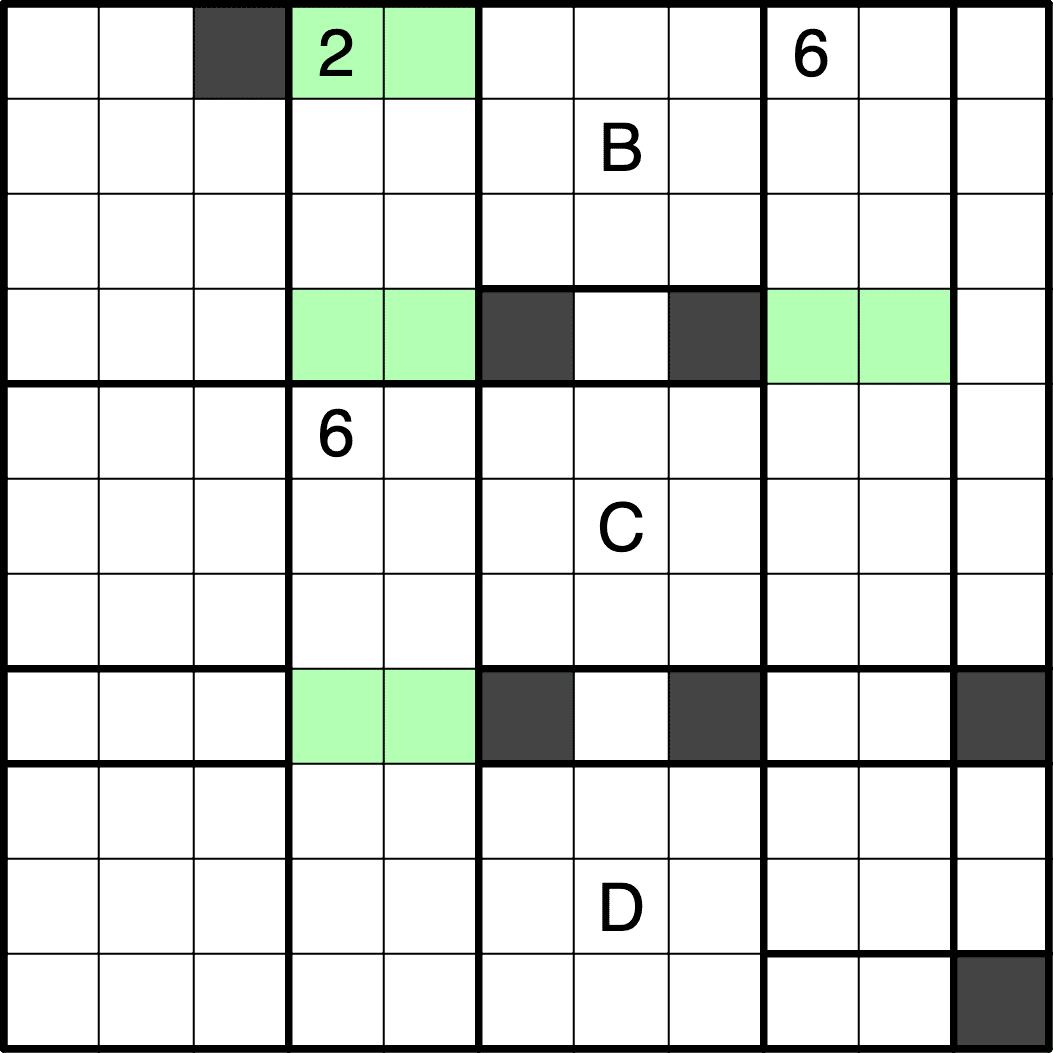
・まず前提として、前述のように、縦の1マスの隙間を通ってBとC、CとDがつながることはできません。
・右の6の部屋の黒マス配置を考えると、BとCのうち右方向に抜けられるのはどちらか一方になります。言い換えると、BとCがつながるためには一度盤面の左側を経由する必要があります。すなわち、盤面の右側から左側に抜ける経路は、2ヶ所必要だということになります。

オレンジの部分はどちらか一方しか通れないので、ピンクのところは分断することができず、2の部屋が決まります。
同様にして、CとDのうち左方向に抜けられるのはどちらか一方であることを考えると、右下の2×2の部屋も、分断が起こらないような配置にする必要があり、以下のようになります。

ここからは難なく解けるはずです。3×3のへやも一意に決まります。三連禁や分断禁に最後まで注意しましょう。
解説は以上になります。お付き合いいただいた方はありがとうございました。
4.不定形について
普通のぜんべやは、へやわけがそうであるように部屋の形が正方形・長方形になっていますが、そうでないものもあり、不定形ぜんべやと呼ばれています。不定形の中でも部屋の形が点対称なものは同じように解けるのでいいのですが、点対称でないものは面倒です。
部屋の形が点対称じゃないのに黒マスの配置が点対称とはどういうことだとなりますよね。
詳しくはY.Y.さんがへやわけ用語の基礎知識βに書いてくださっているのですが、「点対称位置」の解釈については、
「辺が格子に沿ったもので、その部屋を完全に含む長方形をとる。この長方形の中心を対称の中心として、部屋内の全てのマスについて、対称位置(部屋の内外は関係なく、あくまで長方形での対称となる位置)とマスの色が一致する。」(へやわけ用語の基礎知識βより)
となっています。つまり、こういうことが起こりうるんだと思います。

これだけだとまあいいですが、隣接している他の部屋も不定形だった場合に干渉し合うと思うとこわいですね。
なお、「部屋内の全てのマスについて、対称位置(部屋の内外は関係なく、あくまで長方形での対称となる位置)とマスの色が一致する。」なので、長方形に含まれていても対称となる両方の位置が部屋に含まれていなければ、そのマスのことは考えません。以下の焼きもうふさんの例がわかりやすく、真ん中のS字4マスや左上右下は無視するということになりますね。
不定形ぜんべやのルールについて
— 焼きもうふ (@pronter) September 26, 2018
1.三連禁。『白マスの直線部分は、太線を一回までしかまたげない』
2.対称ルール。その部屋を包含する最小の長方形を考えて、その長方形についての対称マスを考える。『どのマスについても、そのマスが属する部屋についての対称マスと白黒が一致する』 pic.twitter.com/3SbKzwtNnI
不定形ぜんべや、自分の部屋の全てのマスに対して対称位置を確認しにいってるだけだから、自部屋の収まる長方形内部でも対称位置が両方部屋の外なら判定されないんだな
— むっき (@mukkitokonbu) October 21, 2020
もともとはぱずぷれのぜんべやの正解判定機能の仕様で、部屋が長方形でない場合にこのルールに沿って黒マスを配置すると正解判定が出たために、このようなルールになったらしいです。
なお、不定形ぜんべやではなく不定形へやわけもあり、これはHeyawacky(Wacky = 奇妙な)としても知られています。命名はmotrisさんのようです。こっちは、同じ部屋であっても連続する白マスが太線を2回またぐことが禁じられている(ことが多い)以外は、特に変わったことはありません。

↑白マスが3つ以上の部屋にわたって続いているわけではないが、これも禁止形とする(ことが多い)
5.不定形ぜんべやに入門してみた
この記事を書くまで不定形ぜんべや何もわからん状態で、見かけてもスルーして来たんですが、せっかくこの記事を書いているのでちょっと触ってみました。(現在12/6未明)
部屋の形が点対称な不定形ぜんべやにもマトリョーシカ川などの手筋(?)が存在しますが、今回は部屋の形が点対称ではないという点について少し考えてみようと思います。

著者が手筋を探って紹介する内容になってしまうので、自分で手筋を探したい方は見ない方がいいかもしれません。探す気のない方は眺めて楽しんでください。
mudoさんがTwitterとパズルスクエアで不定形ぜんべやの問題をたくさん公開されているので、実際に解いてみたい方はこちらに飛んでみるとよいかもしれません。(スレッドに40問ほど問題が続いています。)
不定形∀人∃HEYAその1https://t.co/Jk2e23YHnuhttps://t.co/4Maa1wOOc5
— mudo (@mudopnw) October 19, 2020
勝手に命名
「辺が格子に沿ったもので、その部屋を完全に含む長方形」「その部屋を包含する最小の長方形」と毎回呼んでると疲れるので、「額縁」と呼ぶことにします。

入り口
Lテトロミノ、Uペントミノは単独で入り口になります。

額縁の辺の長さが偶数×奇数である場合は、(額縁の中央2マスのうち少なくとも一方が部屋に含まれていれば)不定形ぜんべやでも中央2マスが白マスになるためです。
右の部屋では決まりますが、左の部屋では中央2マスが部屋に含まれていないので決まりません。

一方で、奇数×奇数の部屋で数字の偶奇により中心のマスの色が決まるという手筋は、不定形では使えません。部屋内のあるマスの点対称の位置にあるマスが部屋に含まれているかはわからないためです。以下の3の部屋は2通りで決まりません。

逆に、奇数×奇数ではない、中心を持たない部屋を考えてみると、部屋内のある1つのマスのみに対して、点対称位置が部屋の外だった場合に、黒マスの数が奇数ならそのマスが黒、偶数ならそのマスが白、というものがあります。

同様に、部屋内のある1つのマスのみに対して、点対称位置が部屋の中だった場合には、黒マスの数が奇数ならそのマスが白、偶数ならそのマスが黒、ということになります。L字は使いやすいかもしれません。

あとは、不定形の部屋ならではの入口はあります。

定形ぜんべやではあるマスが決まるとその点対称位置のもう1ヶ所が決まりますが、不定形ぜんべやで点対称位置が複数ある場合、もっと多くのマスが決まることがあります。
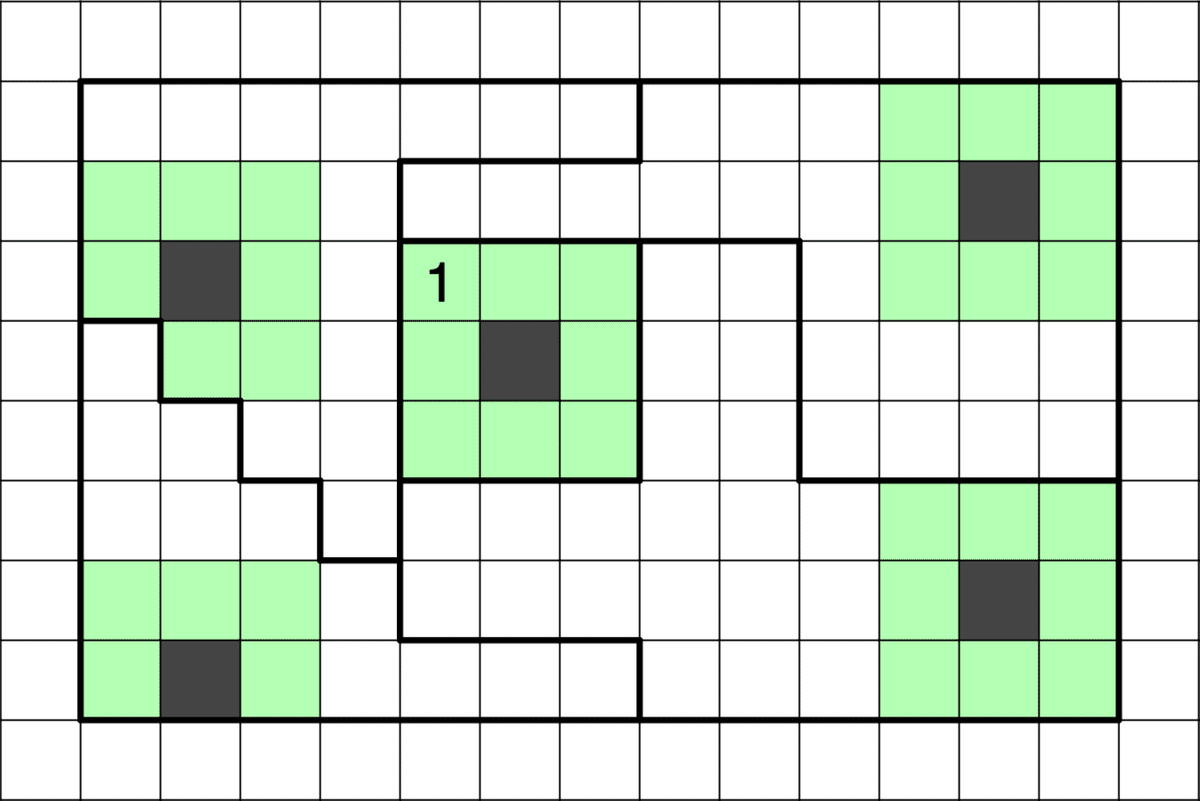
βシート構造
Euexさんが、L字3マスブロックを2つ組み合わせたものは、へやわけの3in2×3と同じになることを発見したとツイートされていました。
不定形∀人∃HEYA、下手につくると思わぬ場所に白マス黒マスが飛んでいって非常に危険なので平和的利用法を考えたところ、図の2ブロックが某へやわけの定番入口だけどと∀人∃HEYAではなかなか使えない手筋と同じ役割を果たすことがわかったことを報告します pic.twitter.com/ph3rYfgm3P
— Euex@無気力 (@Euex) September 15, 2018
これを3×nの部屋に拡張することができます。額縁が2×nになるような2つの部屋同士を組み合わせて3×nの長方形の部屋にすると、こんな感じで、3列の黒マスの並びが交互になるという手筋です。(青マスは決まりません。一例です。)ここからすぐ黒マスの位置が決まるわけではないですが、特に1行目と3行目が同じ色になることは大きなヒントになりそうです。

4列以上に増やしていったら楽しそうだなあと思うのですが、適用できない場合があることに注意です。赤いマスが、真ん中の部屋の額縁には入っていますが部屋とその点対称の位置には入っていないので、赤の2マス同士は同じ並びにはなりません。真ん中の4列について見れば、黒マスの並びは交互になっています。

全ての部屋で、額縁に入っていて部屋とその点対称の位置に入っていないマスがなければ、問題ありません。


ここから少し切り方を変えて、3×nの長方形を額縁が2×(n-k)になる部屋と3×nになる部屋の組み合わせに分けると、黒マスの同じ並びが平行になったりします。(注:額縁が3×nになる部屋と2×nの部屋を組み合わせて3×nの部屋を作ることはできないはずです。)

点対称だったはずがこんな形にできるのはちょっと面白いなと思いました。

中心が額縁3の部屋に含まれるようにすると、同じ色どうしが白黒一致するので、回文のようになります。

回分構造の長さが偶数の場合、中央2マスは白でなければいけないので、

こうなります。なんだこれ...

これはどう決まるでしょうか。
ペンパエディタのリンク
20行下から解説します。

こうなって、(同じ色のマスは白黒が同じになります)

回文になって(右下の長方形の部屋の点対称より)、緑や白を黒マスにすると破綻するので、灰色が黒マスになります。

対称位置の対称位置が隣
点対称の点対称が隣になるとき、白マスが決まります。
下の図を見てください。Aのマスに注目すると、大きい部屋の対称中心は黒丸なので、Aの対称位置はDになります。小さい部屋の対称中心は二重丸なので、Dの対称位置はEになります。ルールからAとDとEの白黒は同じになりますが、AとEは隣り合っているため共に黒になることはできず、共に白であると決まります。
BとCについても同様に考えると、右のところまで白が決まります。

ここからさらに決まります。図の4行目(小さい部屋の一番上の行)で、三連禁のためにFとGの組のうち一方が黒になる必要があるので、いずれにせよHは白になり、右図まで決まります。

これはβシートの特殊な場合ともいえるかもしれません。
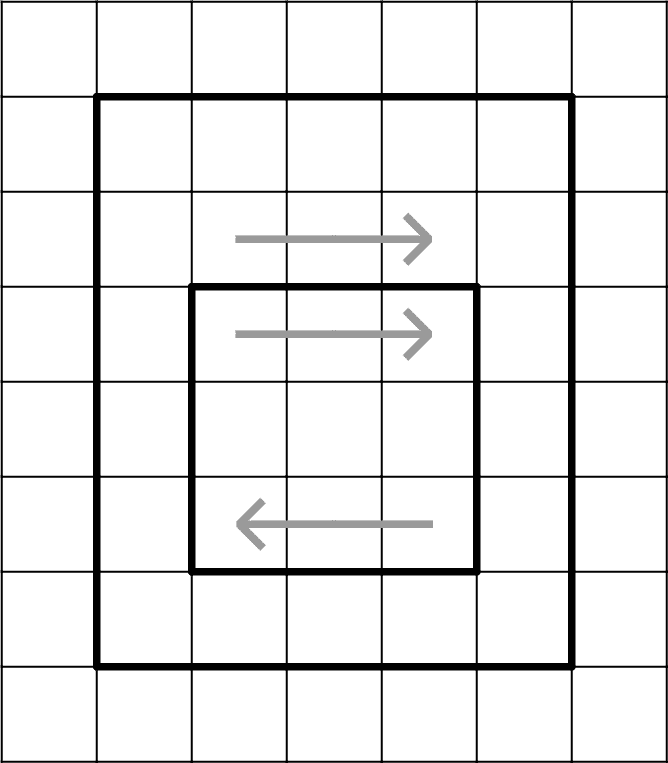
この手筋を色々入れ込めたら面白いのですが、すぐにハタンしてしまって使いづらいのと、解き手目線では1マス1マスに注目する必要があるのでかなり見えにくくなってしまい(先ほど紹介した4問目の入り口のように)、個人的にはあまり入れる気にならないですね。(先ほど紹介した4問目には使いましたが。)

↑いずれも破綻
時間がなく、ここまでしか探せませんでした。また見つけたら報告します。
6.感想
ぜんべやの遠くに波及して大きな展開を作れるところや、点対称の大部屋がきれいなところに良さを感じています。へやわけよりも、(難易度を抑えて)大部屋を作りやすいところも良いですよね。
点対称ルールを生かした面白いパズル/バリアントができないか考え中です。(天体ショーはありますが)何か思いついた人は教えて下さい。
数字なしのへやを作りやすいのもいいところです。ぜんべやに限った話ではないですが、(直接的な)ヒントがないエリアがきっちり決まるのが大好きなんですよね。このあたりについては来年のアドベントにでも書いてみたいと思います。Vanillaiceさんの生命の神秘AqreやPuzzle Square LITSなどがいいねを集めているので、みんな好きなんでしょうかね。(同様の趣向の2作目以降はいいねあんまり集まってないですが...)
不定形ぜんべやについては、一問くらい作って記事に添えようかと思っていたのですがどうにもしっくりきませんでした。自由度が高すぎても困るというのは色々なパズルに対して思うことで、結局何か縛りが欲しくなると部屋の形が長方形という縛りが丁度いいのかなと思いました。人々が点対称配置にこだわるのもそういうことなのでしょうか。
自由度が高すぎて良くないこととして、解くときにヒントが多くないと決まらないようなものはよくないというのはあると思うのですが(例えば四角に切れの、領域の形が四角ルールがなかったら流行らなそう)(四角に切れが流行ってるのかは知りません)、それは不定形ぜんべやを作るときだったり、点対称じゃない問題を作るときの自由度とは別物なような。
齋藤スバルさんの昨年のアドベントカレンダーの記事「制約の環とパズルの質についてふわふわした考察<未完>」では
制約の輪を盤面に入れ込めば入れ込むほど、当然ながら作問の難易度は高くなり自由度は狭まっていきます。だからといって、制約の輪を緩くしすぎてしまうと、先ほどのスケルトンの青マスの部分のように、他の部分とは完全に独立して好きなように入れれてしまい、パズルらしからぬ「恣意性」が出てきてしまうのが難点です。
とありました。なるほど...
不定形ぜんべやは作り始める前は何でもありで困るなと思っていた一方で、実際に作り始めてみると、部屋同士が干渉して決まりすぎてしまう場面があり、仕掛けを入れようとしてもすぐにハタンしてしまったりして制御の難しさも感じました。部屋の境界を波及のしすぎを防げればいいのですが、それもそれでわざわざ不定形ぜんべやにしている意味がないようにも思えたりします。
「わざわざ〜する意味がない」という言葉は、「〜する」ことで何かを犠牲にするときに使う言い回しだよなあと書いてから思ったのですが、今回の場合はそれはぜんべやの点対称の綺麗さかなあと思っています。点対称ではあるけどそれはルール上での話で、人間視点での(?)点対称感がなくなっているという感じも少し残念でした。
「わざわざ(変種)にしている意味がない」というのはバリアントあるあるかもしれません。自分も昔は変なバリアントを考えてはパズルスクエアなどに投稿していたのですが、最近はわざわざバリアントにしてもなあと思いがちです。ニコリのオモパ(読者が考えた新しいパズルを紹介するコーナー、人気が出ると「昇格」してレギュラーパズルになります、へやわけやヤジリンを含む、多くのパズルがこのコーナー出身です)でも、ルールが似たようなものはおそらく載らないでしょうし。この場合に犠牲になっているのは何なんでしょうか、新しいルールを覚える手間とかでしょうか。
自分が斬新なバリアントを解く機会はPuzzle GPが多いのですが、バリアントを生かした手筋を発見することが多くいつもこういうバリアントを作りたいですねと思っています。話が色々なところに飛んですみません。
また、最後の方に書いた「1マス1マスに注目する必要があるのでかなり見えにくくなってしまう」だったり、変な形の部屋で、あるマスが部屋の点対称効果の範囲内なのかどうかわかりにくい、というのは取っ付きにくさの要因かもしれません。

灰マスが部屋の点対称位置、水色マスが関係ないマス
この例だと盤面の真ん中に対称中心が来るように置いてあるのでまだわかりやすいですが
紛れてるとわからなくなります
ここまで不定形ぜんべやのネガキャンを書いてしまったのですが(不定形ぜんべや初心者の分際でごめんなさい)、点対称感がないという話以外は面白い問題を作るのが難しいということに尽きるので、面白い問題が作られることには期待しています。不定形ぜんべやに関してはルール自体はかなり興味深いものだと思うので。解き心地にしても、うまく組み込むのが難しそうですが、上で取り上げたβシート構造のような連鎖は、定形ぜんべやにある良さをさらに伸ばしていると思います。一気に白黒決まると楽しそうですね。
自作の解説で終わるつもりが思いっきり不定形ぜんべやの話になってしまいました。内容は以上になります。長々と失礼しました。
