
数独はPythonで考えて解く話
Naruhikoです。
小さい頃からパズルは大好きでした。
手で触りながら解くパズルや、紙の上で解く頭のパズル。
どれも一気に集中することができ、時間の溶けるもの。
それがパズルです。
家になぜか知恵の輪やルービックキューブなどがたくさんありました。
やっぱり親の影響を受けているんでしょうね。
知らず知らずのうちに解くことに夢中になったんです。
大人になってもパズルは好きで、その中でも数独(ナンプレ)は特に好きです。シンプルなのに奥が深く解けた時の達成感もいいものです。
しかし、今はちょっとパズルに対しての考え方が変わってきました。
解くのも好きですが、解くための方式を考えるのも好きになってきたんです。そうです。パズルを自動で解くことが出来るプログラムを書くことが出来るかですね。
そして自然と数独も自動で解くプログラムがかけるかどうかを考えるようになりました。
実は数独の解き方はいろいろな人がもうやっているんですよね。
それは当然です。人気なパズルですから。
せっかくですので、僕なりのプログラムの書き方をここで公開をしておこうと思います。
プログラム言語はもちろん僕が大好きな Python です。
まずは数独をどうやって解いていこうかを考えてみたいと思います。
数独ってどうやって解いていくの?
人間は数独をどうやって解いているのでしょうか。
解き方はみんな知っていますよね。
9×9マスずつの正方形の中に数字を入れていきます。
1列で数字の重なりがなく、1行にも数字の重なりがなく、
そして3×3マスのブロックの中にも数字の重なりがないように
数字を配置していきます。
例えばこの表です。
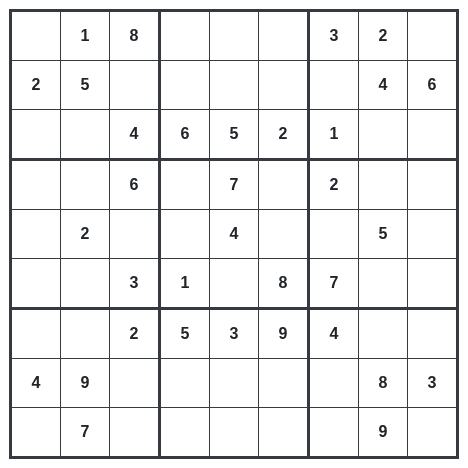
上の3段のブロックを見てみましょう。
5の数字を考えた場合、2段目と3段目には5を入れることができません。
左の3×3のブロックと真ん中の3×3のブロックには5が入っているので
結果的に5が入るのは一番右上のマスになります。
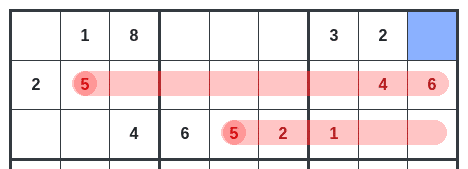
このような感じで重複しない数字をどんどん当てはめていくと
最終的に全てのマスに数字を埋めることができます。
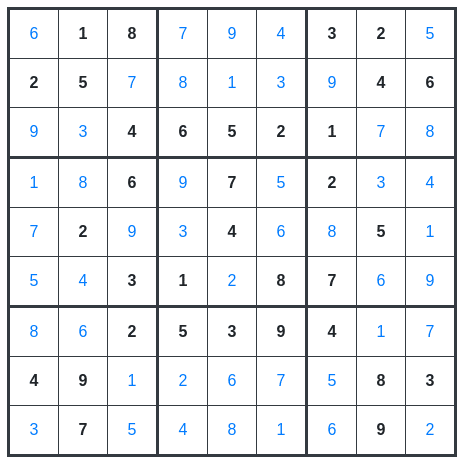
簡単ですね。
このような解き方を「推論する」と言います。
条件を元に推論していくことで数字を決めていくんですね。
人間の思考速度ではこういう解き方が必要になっています。
こういうふうにいろいろな条件を探しながら確定したものをいろいろな角度から探していくのが面白く、数字が埋まったときが嬉しいですよね。
もう一つの解き方
実はもう一つ解き方があります。
それは、「総当り」です。
1から順に当てはめていき、NGの条件になったら戻って次の数字を当てはめて、最終的にNG条件をすべてクリアしたら完成という、気が遠くなるようなやり方です。
1マス目に数字を入れる。
2マス目に数字を入れる。
NG条件にならないかチェックをしてNGなら前のマスの数字を変更する。
OKなら新たに3マス目に数字を入れる。
・・・・
これを繰り返していきます。
どのくらいのパターンがあるか計算するのはやめておきます。
人間がやろうとするととてもじゃないが正解にたどり着けません。
しかし、これはコンピュータの計算能力では可能になるんです。
この「総当り」をプログラムで組んでみる
今回はこの「総当り」をプログラムで組んでみようというものになります。
コンピュータならではの解き方になります。
ここで、どうやって総当りをしたらいいのかを考えてみましょう。
for 文を大量に生成する方法がありますが、それは現実的ではありません。
全部のマスを回そうと思うと大量すぎるのです。
そして、そんな可読性の悪いコードはちょっと遠慮したいですね。
というわけで、今回は再帰的解法というやり方を使ってみます。
再帰的解法とは
再帰的解法とは再帰的にプログラムを回すことで総当りで確認していくという方法です。再帰関数や再帰的なアルゴリズムなどとも呼ばれます。
たとえば、フォルダー内のファイル名を全て取り出したいと考えます。
/folder01
|-- folder02
| |-- file01
| `-- file02
|-- folder03
| |-- folder04
| | |-- file03
| | |-- file04
| | |-- file05
| |-- file06
| `-- file07
|-- file08
|-- file09
`-- file10フォルダー内はファイルとフォルダーと混在しています。
フォルダー内を調べた時にフォルダーがあった場合はまたそのフォルダー内を調べていくという流れになります。
フォルダーの中身を調べるという動作は共通です。
def list(path):
files = フォルダーの中にある一覧
for file in files:
if file == フォルダー:
list(fileのパス) ★
else:
filename.append(fileの名前)
return filename ちょっと適当ですが、こんな感じです。
フォルダーの中のフォルダーを調べるために、自分を実行(★)しています。フォルダーを見つけるたびにフォルダー内を調べるというlist関数を呼び出すことになるのです。
そして調べた結果を返すことで、全てのフォルダーにあるファイルを調べることができます。
実際に数独を解くプログラムを作ってみる
では、今回はこの再帰的解法を使った総当たりをして数独を解いてみましょう。ここからはコードを書いていきます。(いつかは有料にするかもしれません)
本当に数独が作りたくて、pythonを覚えたい人向けです。
まずは何が必要でしょうか。
処理の流れを考えてみましょう。
1.インプット
2.数字を入力するマスを決める
3.数字を入力し、数独の法則に違反していないかチェックする
4.違反していれば巻き戻り、違反していなければ次へ進む
5.すべて埋まるまで繰り返す
6.アウトプット
こんな感じです。
まだ0になっているマスを調べて、数字を順番に入力してみます。
違反していた場合は、その数字を巻き戻して違う数字を当てはめてみます。
もし、どの数字も当てはまらなかった場合は、ひとつ前のマスに戻って数字を入れなおします。
これがすべてのマスに0がなくなるまで繰り返します。
1.インプット
何がともあれ、スタートするには最初の状態を渡さなければなりません。
よく本や雑誌に書いてあるスタート時の虫食い状態がそれです。
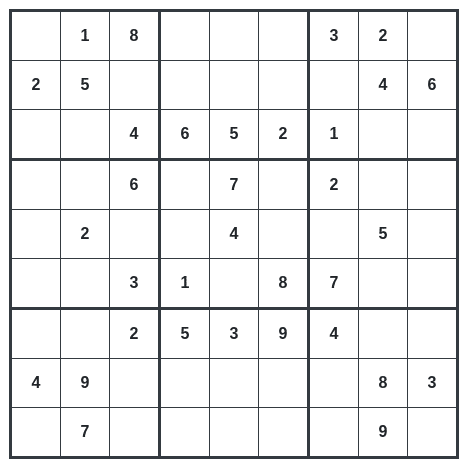
縦9マス横9マスですね。これを配列で表現します。
まずは、縦9マスです。
input_grid = [1行目, 2行目, 3行目, 4行目, 5行目, 6行目, 7行目, 8行目, 9行目]この各行に横9マスを入れる感じですね。
input_grid = [[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目],
[1列目, 2列目, 3列目, 4列目, 5列目, 6列目, 7列目, 8列目, 9列目]]上の表ではこうなります。
input_grid = [[0, 1, 8, 0, 0, 0, 3, 2, 0],
[2, 5, 0, 0, 0, 0, 0, 4, 6],
[0, 0, 4, 6, 5, 2, 1, 0, 0],
[0, 0, 6, 0, 7, 0, 2, 0, 0],
[0, 2, 0, 0, 4, 0, 0, 5, 0],
[0, 0, 3, 1, 0, 8, 7, 0, 0],
[0, 0, 2, 5, 3, 9, 4, 0, 0],
[4, 9, 0, 0, 0, 0, 0, 8, 3],
[0, 7, 0, 0, 0, 0, 0, 9, 0]]0は空白、それ以外は最初から入っている数字です。
2.数字を入力するマスを決める
この数独の目的は、0(空白)のマスに法則に違反しない数字を入れていくことです。0がどこのマスにあるか、なければ終了を返す関数を作成します。
チェックするのは、input_grid を基にした grid という変数を受け取り、その変数の最初の0はどこにあるかを調べます。
grid[0][0] から grid[8][8] まで順番に確認していきます。上の例の場合は初期状態の input_grid なら、[0][0]が返り、grid[0][0] に数字が入れば [0][3] が次の0のマスになります。すべて確認したときに0がなかったら終了を意味する [-1][-1] を返します。
まずは、すべてのマスを調べましょう。
これは簡単ですね。縦と横をそれぞれ for 文で回します。
縦が y、横が x で作っていきます。
range(9) は 0から9個のリストを作ります。
[0, 1, 2, 3, 4, 5, 6, 7, 8]という感じですね。
※python3 ではこのままではリスト形式に変換されません。list(renge(9))でリストとして作成されますが、for 文で使うときはrange(9)で大丈夫です。
関数名は find_next_cell としました。
def find_next_cell(grid):
for y in range(9):
for x in range(9):
print(grid[y][x])
find_next_cell(input_grid)変数 input_grid を渡してみたときに、出力されるのはこうなります。
0
1
8
0
0
0
3
2
0
(続く)すべてのマスの数字を取ってくれるはずです。
次に、もし0が入っていた場合には最初に見つけた y と x を返してみます。
さらに0がなかった場合は y = -1 , x = -1 を返すようにします。
def find_next_cell(grid):
for y in range(9):
for x in range(9):
if grid[y][x] == 0:
# 0 の座標を返す
return y, x
# すべてのマスに数字が入っている状態
return -1, -1
y, x = find_next_cell(input_grid)
if y == -1 or x == -1:
print("すべてのマスに数字が入力されています")
else:
print(y, x)input_grid によって返ってくる値が違うと思います。
簡単なリストを渡してみましょう。
input_grid = [[0, 1, 8, 0, 0, 0, 3, 2, 0],
[2, 5, 0, 0, 0, 0, 0, 4, 6]]
=> 0 0input_grid = [[1, 1, 8, 0, 0, 0, 3, 2, 0],
[2, 5, 0, 0, 0, 0, 0, 4, 6]]
=> 0 3input_grid = [[1, 1, 8, 2, 3, 4, 3, 2, 5],
[2, 5, 0, 0, 0, 0, 0, 4, 6]]
=> 1 2input_grid = [[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9],
[9, 9, 9, 9, 9, 9, 9, 9, 9]]
=> すべてのマスに数字が入力されていますうまくいきましたか?
0が存在する限りそのマスを返すことができれば成功です。
3.数字を入力し、数独の法則に違反していないかチェックする
数独の法則をもう一度確認しましょう。
①同じ行には同じ数字が入らないこと
②同じ列には同じ数字が入らないこと
③同じブロック(3×3)には同じ数字が入らないこと
最初に関数を作ります。
違反していないなら True、違反しているなら False を返します。
関数名は「有効チェック」を行うということで is_valid にします。
def is_valid(grid, y, x, value):
pass引数は、grid、y座標、x座標、それから、入力する数字valueです。
grid の [y][x] の座標に value を入れた場合、その数字が有効かを調べます。
①同じ行には同じ数字が入らないこと
同じ行とは、yが同じマスになります。grid[y] を指定すると、list形式で取得できるはずです。そして、そのリストの中に value と同じ数字がないかチェックします。
このチェック(is_row)にも in 演算子を使います。
そして not を入れることでリストの中になければ True を返すようにします。
def is_valid(grid, y, x, value):
# 行のチェック
is_row = value not in grid[y]
return is_row②同じ列には同じ数字が入らないこと
次に同じ列に同じ数字がないかをチェックします。
これはちょっと変則です。
x 番目の列を取り出すのですが、for 文を使います。
x = 1
lst =[]
for i in input_grid:
lst.append(i[x])
print(lst)
=> [1, 5, 0, 0, 2, 0, 0, 9, 7]こうすると指定した x 番目の列をリストにすることができます。
でも、python では便利なリスト内包表記というものがあり、1行で作ることが可能です。それがこちら。
x = 1
lst = [i[x] for i in input_grid]
print(lst)
=> [1, 5, 0, 0, 2, 0, 0, 9, 7]for 文を1行で表すことができるんです。
これを使って縦のチェック(is_column)を追加します。
def is_valid(grid, y, x, value):
# 行のチェック
is_row = value not in grid[y]
# 列のチェック
is_column = value not in [i[x] for i in grid]
return all([is_row, is_column])bool型(True, False)は、all()関数を使うことで、全て True だと True を、どれかが False の場合は False を返します。
縦横両方が数字が入っていない状態(True)になっている場合のみ True を返します。
③同じブロック(3×3)には同じ数字が入らないこと
同じブロックを計算するにはどうすればいいでしょうか。
9マスのうちの3つのセットなので、1ブロックが0,1,2マス目、2ブロックが3,4,5マス目、3ブロックが6,7,8マス目になることがわかります。
それぞれのブロックが最初の数字になるようにするとあとでの計算がしやすくなります。
0, 1, 2 => 0
3, 4, 5 => 3
6, 7, 8 => 6
という風にしたいと思います。
python では、割り算をするときに、// と2つすると、小数点以下は除去されます。それを使うことで上記のような結果にすることができます。
for i in range(0, 9):
print(i, "=>", (i//3) * 3)
0 => 0
1 => 0
2 => 0
3 => 3
4 => 3
5 => 3
6 => 6
7 => 6
8 => 6数字を 3 で割り、余りを削除して 3 をかけています。
これを縦横のブロック開始値に代入してみます。
blk_x, blk_y = (x//3) * 3, (y//3) * 3さらにこの数字を使って、3×3の内容を取得してみましょう。
便利なライブラリもありますが、今回は使わないようにします。
まずは、対象の3行を取得します。
これはスライスを使ってみます。リスト[開始:終了]とすると、その間の値が取れます。
x, y = 1, 1
blk_x, blk_y = (x//3) * 3, (y//3) * 3
# ブロック行を取り出す
blk_grid = input_grid[blk_y:blk_y + 3]
print(blk_grid)
[[0, 1, 8, 0, 0, 0, 3, 2, 0], [2, 5, 0, 0, 0, 0, 0, 4, 6], [0, 0, 4, 6, 5, 2, 1, 0, 0]]0ブロック行を取得できました。
次はこれに列もブロックで切り取ります。
やり方は、 blk_grid のリストを for 文で回して取得したリストをスライスします。
# ブロック列を取り出す
print([i[blk_x:blk_x + 3] for i in blk_grid])
[[0, 1, 8], [2, 5, 0], [0, 0, 4]]2つをまとめるとこんな感じです。
x, y = 1, 1
blk_x, blk_y = (x//3) * 3, (y//3) * 3
# ブロックを取り出す
blk_grid = [i[blk_x:blk_x + 3] for i in input_grid[blk_y:blk_y + 3]]
print(blk_grid)
[[0, 1, 8], [2, 5, 0], [0, 0, 4]]次に判定するために取得した2次元リストを1次元に直します。
sum 関数を使うことでこれが実現できます。
print(sum(blk_grid, []))
[0, 1, 8, 2, 5, 0, 0, 0, 4]あとはこれを①②と同じようにチェックとして使いましょう。
def is_valid(grid, y, x, value):
# 行のチェック
is_row = value not in grid[y]
# 列のチェック
is_column = value not in [i[x] for i in grid]
# ブロックを取り出す
blk_x, blk_y = (x//3) * 3, (y//3) * 3
blk_grid = [i[blk_x:blk_x + 3] for i in grid[blk_y:blk_y + 3]]
# ブロックのチェック
is_block = value not in sum(blk_grid, [])
# 有効チェック
return all([is_row, is_column, is_block])これで有効チェックの関数が完成しました。
4.違反していれば巻き戻り、違反していなければ次へ進む
ここからは実際に数字を入れてループする処理を作っていきましょう。
これまで2つの関数を作りました。
・空白マスの座標の取得 [find_next_cell]
・有効チェック [is_valid]
これを使い、新たな関数を作っていきましょう。
次に作るのは、座標を取得して実際に数字を入れてみて有効かどうかをチェックするものです。
関数名は解決するという意味の solve_sudoku としました。
引数は grid です。
戻り値は成功か失敗かがわかるように True と False を返すようにしました。
def solve_sudoku(grid):
return true最初は input_grid を渡すことになります。
print(solve_sudoku(input_grid))
[print(i) for i in input_grid]
True
[0, 1, 8, 0, 0, 0, 3, 2, 0]
[2, 5, 0, 0, 0, 0, 0, 4, 6]
[0, 0, 4, 6, 5, 2, 1, 0, 0]
[0, 0, 6, 0, 7, 0, 2, 0, 0]
[0, 2, 0, 0, 4, 0, 0, 5, 0]
[0, 0, 3, 1, 0, 8, 7, 0, 0]
[0, 0, 2, 5, 3, 9, 4, 0, 0]
[4, 9, 0, 0, 0, 0, 0, 8, 3]
[0, 7, 0, 0, 0, 0, 0, 9, 0]戻り値の solve_grid はまだ何も処理をしていないので input_grid と同じになります。
では次に空白のマスを探しましょう。find_next_cell を使います。
y, x = find_next_cell(grid)これで空白のセルを取得することができましたね。
さらに、終了条件である空白がなくなったときに返ってくる値は、
y == -1 または x == -1 でした。(両方 -1 になりますが、どちらかという条件にしています)
この状態のときに True を返します。
def solve_sudoku(grid):
y, x = find_next_cell(grid)
# 終了判定
if y == -1 or x == -1:
return True
return False
再帰処理で一番気をつけることは、最終的に終了する条件を忘れずに必ず入れることです。入れ忘れると一生再帰を繰り返します。
ですので、必ず終了条件から書くようにしましょう。
では、まずは最初に取得したマスに数字を入れてみましょう。
関数内に下記を追加し実行してみます。
def solve_sudoku(grid):
y, x = find_next_cell(grid)
# 終了判定
if y == -1 or x == -1:
return True
# 入力
value = 1
grid[y][x] = value
return True
True
[1, 1, 8, 0, 0, 0, 3, 2, 0]
[2, 5, 0, 0, 0, 0, 0, 4, 6]
[0, 0, 4, 6, 5, 2, 1, 0, 0]
[0, 0, 6, 0, 7, 0, 2, 0, 0]
[0, 2, 0, 0, 4, 0, 0, 5, 0]
[0, 0, 3, 1, 0, 8, 7, 0, 0]
[0, 0, 2, 5, 3, 9, 4, 0, 0]
[4, 9, 0, 0, 0, 0, 0, 8, 3]
[0, 7, 0, 0, 0, 0, 0, 9, 0]最初のマスに1が入りました。
しかしよく見ると同じ行に1がありますね。
これでは有効ではありません。
実際に有効チェックの確認をしてみます。
# 入力
value = 1
print(is_valid(grid, x, y, value))
grid[y][x] = value
return True
FalseFalse ですので、有効な数字ではありません。
今度は、1 ~ 9 を順番に入れて、有効な数字になったら return してみましょう。
# 入力
for value in range(1, 10):
if is_valid(grid, y, x, value):
grid[y][x] = value
return True
return False
True
[6, 1, 8, 0, 0, 0, 3, 2, 0]
[2, 5, 0, 0, 0, 0, 0, 4, 6]
[0, 0, 4, 6, 5, 2, 1, 0, 0]
[0, 0, 6, 0, 7, 0, 2, 0, 0]
[0, 2, 0, 0, 4, 0, 0, 5, 0]
[0, 0, 3, 1, 0, 8, 7, 0, 0]
[0, 0, 2, 5, 3, 9, 4, 0, 0]
[4, 9, 0, 0, 0, 0, 0, 8, 3]
[0, 7, 0, 0, 0, 0, 0, 9, 0]for 文で1から順番に有効チェックし、有効な数字が見つかったらマスに数字を入れて return しました。
この場合は、6が一番早い有効な数字になりましたね。
数字が入ったので次に進みましょう。
これからは同じ処理をすることになります。
ここで初めて再帰処理を使ってみましょう。
再帰処理は簡単です。自分を指定すればいいだけです。
戻り値が True だったら、次のマスへ進みます。
戻り地が False だったら、False を返して終了してみましょう。
# 入力
for value in range(1, 10):
if is_valid(grid, y, x, value):
grid[y][x] = value
# 次へ
if solve_sudoku(grid):
return True
return False
有効性を確認して True だったら、そのマスに有効な数字を入力し、また solva_sudoku を呼び出しています。このときは新しいマスが find_next_cell で取得できるはずです。
そして、-1 になった時点で True になり一番最初まで戻ります。
もし、有効な数字がなかった場合は、False を返しました。
実行して返ってきたものはこれになります。
False
[6, 1, 8, 4, 9, 7, 3, 2, 5]
[2, 5, 7, 3, 8, 1, 9, 4, 6]
[9, 3, 4, 6, 5, 2, 1, 7, 8]
[1, 8, 6, 9, 7, 5, 2, 3, 4]
[7, 2, 9, 0, 4, 0, 0, 5, 0]
[0, 0, 3, 1, 0, 8, 7, 0, 0]
[0, 0, 2, 5, 3, 9, 4, 0, 0]
[4, 9, 0, 0, 0, 0, 0, 8, 3]
[0, 7, 0, 0, 0, 0, 0, 9, 0]随分先まで行きましたが、x = 3, y = 4 で有効な数字がなくなったようです。
このような状態になったときはどうしたら良いでしょうか。
戻りが True でなかった場合は、一つ巻き戻って次の数字を入れるようにします。
しかし、ここでは一つ前のマスがどこか情報がないですよね。
ですので、再帰するときに今のマスを一緒に渡し、そのマスをやり直すことになります。
これは True になるまで巻き戻るため、もしかしたら最初のマスまで戻るかもしれません。そして、次の数字を入れて再開していきます。
def solve_sudoku(grid, y=0, x=0):
...
if solve_sudoku(grid, y, x):これで次の関数へ今のマスの情報を渡すことができます。
y と x に初期値を与えたのは、スタート時に引数を指定しなくても良いようにです。
さらに、巻き戻るときは入力した値をリセットしましょう。
最終的にこのようになりました。
def solve_sudoku(grid, y=0, x=0):
y, x = find_next_cell(grid)
# 終了判定
if y == -1 or x == -1:
return True
# 入力
for value in range(1, 10):
if is_valid(grid, y, x, value):
grid[y][x] = value
# 次へ
if solve_sudoku(grid, y, x):
return True
grid[y][x] = 0
return False5.すべて埋まるまで繰り返す
さて、これでどうなるでしょうか。
True
[6, 1, 8, 7, 9, 4, 3, 2, 5]
[2, 5, 7, 8, 1, 3, 9, 4, 6]
[9, 3, 4, 6, 5, 2, 1, 7, 8]
[1, 8, 6, 9, 7, 5, 2, 3, 4]
[7, 2, 9, 3, 4, 6, 8, 5, 1]
[5, 4, 3, 1, 2, 8, 7, 6, 9]
[8, 6, 2, 5, 3, 9, 4, 1, 7]
[4, 9, 1, 2, 6, 7, 5, 8, 3]
[3, 7, 5, 4, 8, 1, 6, 9, 2]おお!一瞬で出てきました。
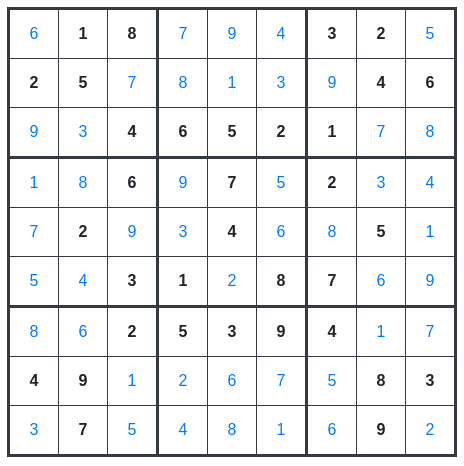
同じ数字になっていると思います。
この関数を使えば、総当たりで数字を調べてくれるのでどんな問題でも対応できるでしょう。
おまけ
ちなみに、どれくらい巻き戻りが発生したか気になりませんか?
難しい問題は巻き戻りも多いのでしょうか。
というわけで、バックトラック(やり直し)を数えてみましょう。
backtracks = 0
def solve_sudoku(grid, y=0, x=0):
global backtracks
y, x = find_next_cell(grid)
# 終了判定
if y == -1 or x == -1:
return True
# 入力
for value in range(1, 10):
if is_valid(grid, y, x, value):
grid[y][x] = value
# 次へ
if solve_sudoku(grid, y, x):
return True
backtracks += 1
grid[y][x] = 0
return False
print(solve_sudoku(input_grid))
print(backtracks)戻り値が True ではなかった場合に、巻き戻る前に backtraks をカウントアップしています。
そして実際の実行結果がこちら。
True
220少ないと見るべきか、多いと見るべきか。
一度超難問の問題を解かせてみたいですね。
最後に
ここまでうまく出来たでしょうか。
ステップごとに説明しましたが、わからないところもあるかもしれません。
その場合は note でも twitter でも質問していただけたら答えます。
どんどん絡んできてください。
最後に、今回のすべてのコードを載せておきます。
ありがとうございました。
backtracks = 0
input_grid = [[0, 1, 8, 0, 0, 0, 3, 2, 0],
[2, 5, 0, 0, 0, 0, 0, 4, 6],
[0, 0, 4, 6, 5, 2, 1, 0, 0],
[0, 0, 6, 0, 7, 0, 2, 0, 0],
[0, 2, 0, 0, 4, 0, 0, 5, 0],
[0, 0, 3, 1, 0, 8, 7, 0, 0],
[0, 0, 2, 5, 3, 9, 4, 0, 0],
[4, 9, 0, 0, 0, 0, 0, 8, 3],
[0, 7, 0, 0, 0, 0, 0, 9, 0]]
def find_next_cell(grid):
for y in range(9):
for x in range(9):
if grid[y][x] == 0:
# 0 の座標を返す
return y, x
# すべてのマスに数字が入っている状態
return -1, -1
def is_valid(grid, y, x, value):
# 行のチェック
is_row = value not in grid[y]
# 列のチェック
is_column = value not in [i[x] for i in grid]
# ブロックを取り出す
blk_x, blk_y = (x//3) * 3, (y//3) * 3
blk_grid = [i[blk_x:blk_x + 3] for i in grid[blk_y:blk_y + 3]]
# ブロックのチェック
is_block = value not in sum(blk_grid, [])
# 有効チェック
return all([is_row, is_column, is_block])
def solve_sudoku(grid, y=0, x=0):
global backtracks
y, x = find_next_cell(grid)
# 終了判定
if y == -1 or x == -1:
return True
# 入力
for value in range(1, 10):
if is_valid(grid, y, x, value):
grid[y][x] = value
# 次へ
if solve_sudoku(grid, y, x):
return True
backtracks += 1
grid[y][x] = 0
return False
print(solve_sudoku(input_grid))
print(backtracks)
[print(i) for i in input_grid]この記事が気に入ったらサポートをしてみませんか?
