
Pure 34437へやわけ 想定解法の詳細解説

はじめに
しろくろみどりん(@sk_midorinP)です。
この記事は、第4回シンデレラパズル総選挙に投稿した「へやわけ for 三好紗南」の想定解法の解説となっています。
皆さまの応援のおかげで、この問題は第4回シンデレラパズルの座に輝くことができました。本当にありがとうございました。
今後とも、私の担当アイドルが一人、三好紗南をよろしくお願いします。
なお、今回の解説は、かなり詳細に書いていますので、へやわけを解き慣れている方には少々冗長かもしれません。ご了承ください。
前提知識
まずは今回の解説にあたって必要となる、手筋の前提知識について。
ヒントの方にも書きましたが、今回の問題は、へやわけの黒マス最密充填における理詰めのフレームワークのひとつである「ペナルティ理論」を活用すると楽になる問題となっています。
この理論については、まり餡さんがわかりやすくまとめていますので、まずはこちらをご覧ください。以降は、このまとめの内容を前提知識として話を進めていきます。
今後解説内に出てくる「第一種~第三種ペナルティ」も、このまとめ内の例題解説に準拠します。
https://twitter.com/agnomy/status/1246741741777997824
なお、上記のまとめは一辺が偶数の正方形盤面を対象にしていますが、この理論は現在、一般的な長方形盤面に拡張されています。今回は使いませんが、一般化した方についてはChaotic Puzzlesさんのまとめをご覧ください(英語です)。
https://twitter.com/chaotic_puzzles/status/1259012122878423041
また、解説の進行にあたり、「へやわけ用語の基礎知識β」に掲載されている用語を使用します。解説内で用いる用語には都度リンクを張りますが、こちらにもページへのリンクを張っておきます。
https://seesaawiki.jp/pencilpuzzle/d/%A4%D8%A4%E4%A4%EF%A4%B1%CD%D1%B8%EC%A4%CE%B4%F0%C1%C3%C3%CE%BC%B1%A6%C2
ヒントのおさらい
こちらが今回投稿したPure 34437へやわけです(再掲)。

盤面に表出されている数字を足し合わせると3+4+4+3+7=21、つまり21個の黒マスを8×8盤面に充填する問題となっています。
これを先程紹介したペナルティ理論に照らし合わせると、21個は8×8盤面に配置できる黒マスの最大数であり、このとき盤面に2個のペナルティが配置されることがわかります。
さて、ペナルティ理論を利用する問題では、「どこにペナルティが配置されるか?」が非常に重要な情報となります。
この問題でも、2個のペナルティがどこに入るかを探すことが理詰めのメインになっています(同時に、最も重い部分がここです)。
ここまでがヒントに書いていた事項です。
なお、以降の解説では、確定したペナルティを赤枠で示すことにします。
① 局所手筋を使って2つの「4」部屋を埋める
まり餡さんによるペナルティ理論解説の例題では、表出でわかりやすくペナルティの位置が示されていましたが、この問題はそうではありません。
そのため、まずは一般的な局所手筋を活用して盤面を埋めていき、その中でペナルティを探すことにします。
まず、2つある「4」部屋のうち、左側の部屋に着目してみると、「腹の白」および「足元の白」により、部屋の両隣の白マスがいくらか確定します。

次に、右側の「4」部屋に着目してみましょう。

分断禁ルールを考えると、青枠で示した2×3空間には黒マスを3個入れることができません。
また、青枠以外の部分にも高々2個しか黒マスが入らないことが自明にわかります。従って、右上の「4」部屋は、青枠部分に2個、青枠以外の部分に2個黒マスが入ることが確定します。

青枠以外の部分に黒マスを2個入れるパターンは1通りしかないため、画像のように黒マスが2個確定します。

これにより左側の「4」部屋の黒マスの配置が確定し、画像の赤枠で示した位置に第二種ペナルティが発生します。
残るペナルティは1つ。

分断禁ルールを考えると、右上の「4」部屋の残り部分も確定します。
② 2つ目のペナルティを探す
ここがこの問題のメインです。
先程、右側の「4」部屋で使った通り、角に接する2×3空間には、黒マスを3つ入れることができません。これを左側の2つの「3」部屋に適用すると、

画像の青枠で示した領域に、1つずつ黒マスが入ることが確定します。これは疑似的な2 in 2×2とみなすことが可能です。
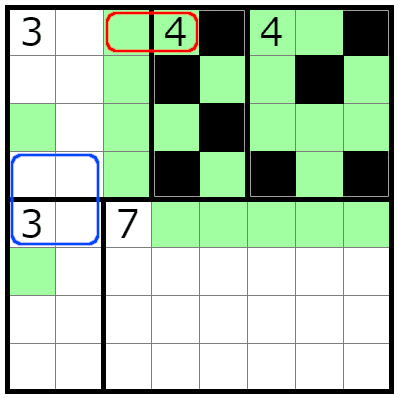
これにより「足元の白」手筋を用いて白マスが2つ確定します。
ただし、今回のケースでは、この白マスの確定よりも、青枠で示した「疑似的な2 in 2×2領域を作ることができる」ことそれ自体が重要になります。
この疑似的な2 in 2×2への黒マスの入れ方は2通りありますが…


この通り、どちらのパターンであっても、左辺に第二種ペナルティが発生します。従って、

上辺の赤枠に第二種ペナルティが一つ、左辺のピンク枠のどこかに第二種ペナルティが一つ発生することが明らかになりました。
③ 仕上げ
これまでの議論で2つのペナルティを使い切りました。
よって、この後にすべきことは、それ以外の場所にペナルティが発生しないように黒マスを埋めていくことだけです(※)。
もはやここまで進んでしまえばあとは作業であり(※)、進め方もいくらでもありますが、とりあえず進行の一例を示していくこととします。各図の青枠を見てください。
(※)あくまで「この問題に関しては」という話です。一般的には、全てのペナルティを使い切ってもある程度の試行錯誤を要する場合も多いです。
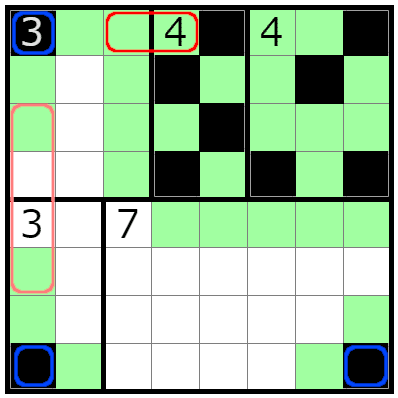
まずは第一種ペナルティを回避するため盤面の角に黒マスを配置。
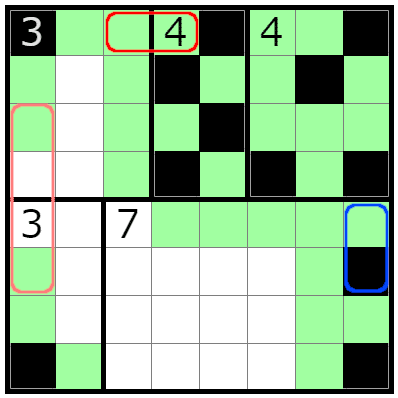
第二種ペナルティの回避。

第三種ペナルティの回避。

再び第三種ペナルティの回避。
ここで、予約していた2つ目のペナルティの位置が確定します。
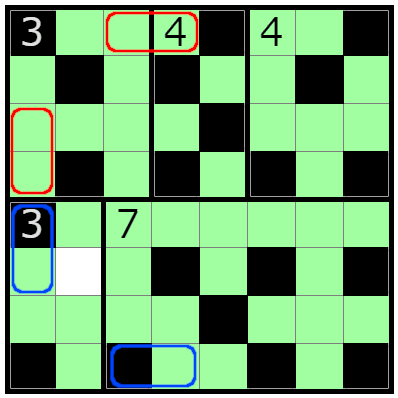
今度は第二種ペナルティの回避。
あとは残った1マスを埋めて完成です。

お疲れさまでした。
