なかなかとけないといたんたん
あけましておめでとうございます。
絶賛灰コーダど真ん中でにょきにょきくねくねしているガガンボもごぼんが、なかなか解けない問を淡々と紹介します。
簡単な問題なので、おやつ程度に見ていってくださいまし。
さて、次の問題を考えます。
Knight Fork の名前は、おそらくチェスのナイトフォークから来ているように思われます。(問題文に含まれる参考の図もナイトの動き方になっています。)
ナイトフォークってなんぞや。 私、気になります。
チェスのナイトは問題文に示されている通り、黒ポチから白ポチに移動することができます。2マス直進したあと、右か左に1マスだけ移動するイメージです。
ナイトが動けるマスは下の図の通りです。
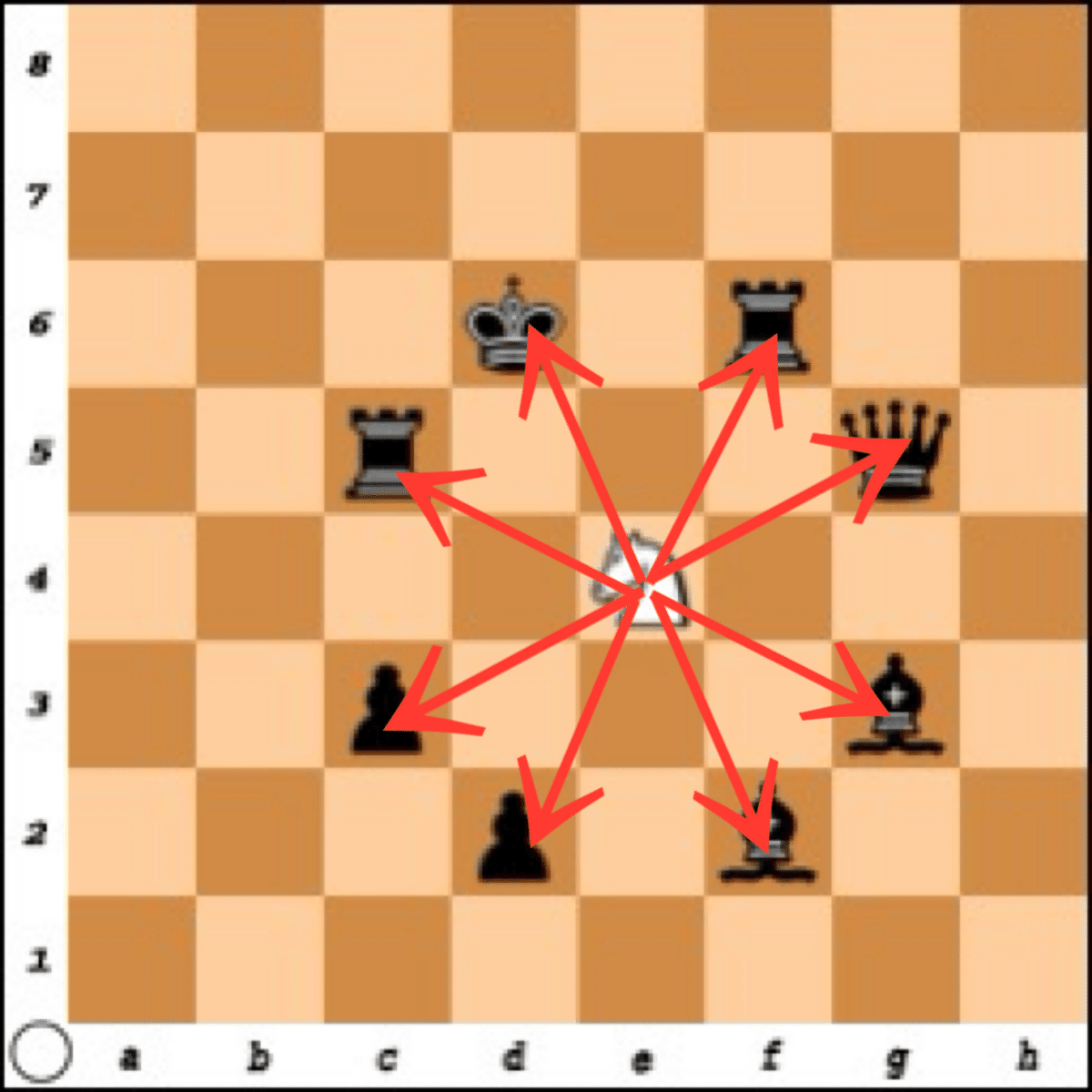
(© Chessvideos.TV)
上図で、白のナイトは黒色のコマを1回の移動で取得することができます。
ただし、もごぼんはチェスを全く知らないのでこのような盤面が存在し得るかはわかりません。(馬がナイトだと思います。多分。)
下図の盤面だと、白のナイトの移動先に黒いコマがあります。
白のナイトは2つの黒いコマのどちらかを好きに取れます。

(© Chessvideos.TV)
f6マスにあるキング(K)、c3マスにあるクイーン(Q)、どちらも射程範囲内です。
このように、ナイトが両方のコマに効いている状態をナイトフォークというようです。(間違っていたら教えてください。)
将棋でいうとこの、「角がこっちにも効いてる」みたいな感じですね。ふーん。
チェスをやってみたくなってきたところで、本題に戻りましょう。
考えたこと
距離が等しい点は、2点の垂直二等分線上にあるけど。。。うん?
もごぼんはよくとんちんかんなことを考えます。
図形の性質的な話であり、解法に結び付きません。
格子点だと多分、1:2:√5の直角三角形になるしかないな。
多分そうだろう。
そうだと信じてる。
「あれがデネブ、アルタイル、ベガ」
書いたコードがこちら。
x1,y1,x2,y2 = map(int,input().split())
def euc2(x1,y1,x2,y2):
return (x1-x2)**2 + (y1-y2)**2
# 2点が離れすぎているケース
if euc2(x1,y1,x2,y2)**2 > 20:
exit(print('No'))
# 1:2:5の直角三角形を考える
p11 = euc2(x1,(x1 + 1),y1,(y1+2)) == 5
p12 = euc2(x2,(x2 + 1),y2,(y2+2)) == 5
if p11 and p12:
exit(print('Yes'))
p21 = euc2(x1,(x1 + 1),y1,(y1 + 2)) == 5
p22 = euc2(x2,(x2 - 1),y2,(y2 - 2)) == 5
if p21 and p22:
exit(print('Yes'))
p31 = euc2(x1,(x1 - 1),y1,(y1 - 2)) == 5
p32 = euc2(x2,(x2 + 1),y2,(y2 + 2)) == 5
if p31 and p32:
exit(print('Yes'))
p41 = euc2(x1,(x1 - 1),y1,(y1 - 2)) == 5
p42 = euc2(x2,(x2 - 1),y2,(y2 - 2)) == 5
# ... ... ... ... ... ... ... ... ... ... ... #
# ... ... ... . 60行くらい続く ... ... ... ... #
# ... ... ... ... ... ... ... ... ... ... ... #書いていた時は、何を考えていたのでしょうか。頭のなかを覗いてみましょう。おーい、のうみそくーん。
頭の中「プラス、マイナス、プラス、マイナス、プラス、プラス、プラス、マイナス、プラス、マイナス、マイナス、マイナス、…」
大丈夫でしょうか。
Waiting Judge…
…
…
…
…誤答になりました。

(https://bocchi.rocks/omnibus/special/x69gif/)
GO TO BED。 METTYA TOO BAD。
突き詰めると、コマの置き方は、
(x1,y1) から2×2マス四方だけを考えればいいことがわかります。
# 入力
x1,y1,x2,y2=map(int,input().split())
# ユークリッド距離の2乗
def euc2(x1,y1,x2,y2):
return (x1-x2)**2+(y1-y2)**2
# (x1,y1)から2×2マス四方だけ考えれば十分である
# (自分へ)
# "四方"という言葉ばかりに囚われすぎると,
# range(x1-2,x1+2)と書いてしまうので注意してね
# (x,y)を固定する
for x in range(x1-2, x1+2 +1):
for y in range(y1-2, y1+2 +1):
if euc2(x1,y1,x,y) == euc2(x2,y2,x,y) == 5:
exit(print('Yes'))
print('No')#include <iostream>
using namespace std;
// ユークリッド距離の2乗
int euc2(int x1, int y1, int x2, int y2) {
return (x1 - x2) * (x1 - x2) + (y1 - y2) * (y1 - y2);
}
int main() {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
// (x, y)を固定する
for (int x = x1 - 2; x <= x1 + 2; x++) {
for (int y = y1 - 2; y <= y1 + 2; y++) {
if (euc2(x1, y1, x, y) == 5 && euc2(x2, y2, x, y) == 5) {
cout << "Yes" << endl;
return 0;
}
}
}
cout << "No" << endl;
}この手の必要な部分だけを考える全探索、ちょっとトリッキーに感じて、まだ慣れません。
サラサラ書くのはまだ難しいので、刷り込んでいきたいです。
また、ナイトを2回動かすのを全探索する解法もあります。(解説より)
ん、なんでぇ?
これを、解説の方言で書いてみると、
もし、条件を満たすなら、(x1,y1), (x2,y2) はナイトフォークできる2つのコマの座標である。
このとき、次が成り立つ。
「(x1,y1) の位置から2回ナイトを動かして(x2,y2)にたどりつく」
これを判定しましょう。
となります。
図も見ておきます。
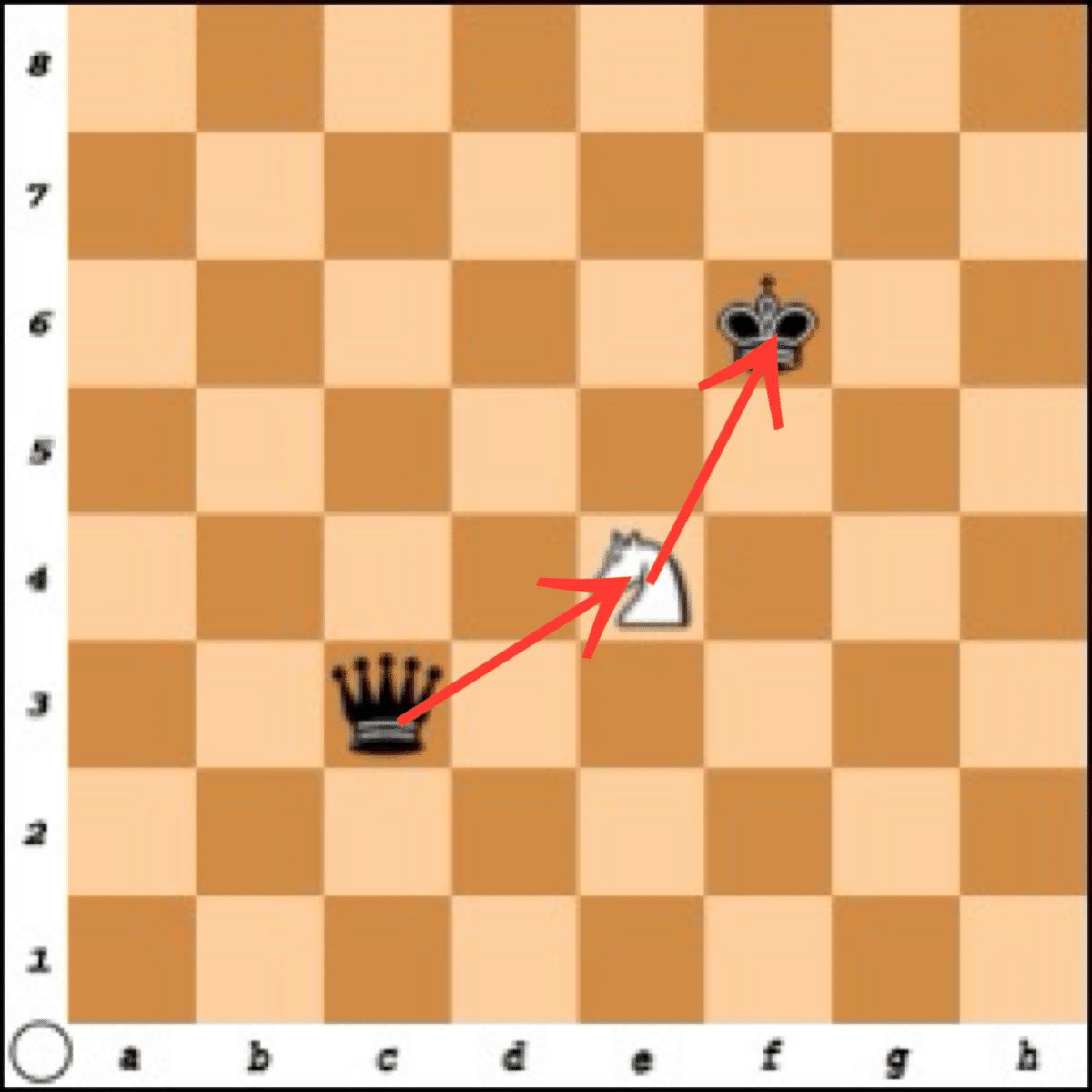
(ナイトをc3から2回動かしてf6に到達する)
先ほど出した、ナイトフォークの図に赤矢印を付け足したものです。
この状態なら、たしかに、ナイトは1つ目のコマの座標(x1,y1)から2回ジャンプして、2つ目のコマの座標(x2,y2)に辿り着きます。
2回の移動は2重ループで表現してあげればいいですよん。
書いたコードはこちら。
# 入力
x1,y1,x2,y2=map(int,input().split())
# ナイトの動き方
move = [(+2,+1),
(+2,-1),
(-2,+1),
(-2,-1),
(+1,+2),
(+1,-2),
(-1,+2),
(-1,-2),
]
# もし、条件を満たすなら、
# (x1,y1), (x2,y2) はKnight Forkできる2つのコマの座標である
# このとき、次が成り立つ
# 「(x1,y1) の位置から2回ナイトを動かして(x2,y2)にたどりつく」
# これを判定しよう
# 2回の動きを固定
for move1 in move:
for move2 in move:
if x1+move1[0]+move2[0]==x2 and y1+move1[1]+move2[1]==y2:
exit(print('Yes'))
print('No')
#include <iostream>
using namespace std;
int main() {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
// ナイトの動き方
int move[8][2] = {
{+2, +1}, {+2, -1}, {-2, +1}, {-2, -1},
{+1, +2}, {+1, -2}, {-1, +2}, {-1, -2}
};
// 2回の動きを固定
for (int i = 0; i < 8; i++) {
for (int j = 0; j < 8; j++) {
int nx = x1 + move[i][0] + move[j][0];
int ny = y1 + move[i][1] + move[j][1];
if (nx == x2 && ny == y2) {
cout << "Yes" << endl;
return 0;
}
}
}
cout << "No" << endl;
}
以上であります!
読んでくれてありがとうであります!
ばい!
