
並木中等教育学校サイエンスカフェ「正五角形と三角比の関係」開催記録
今回は、並木中等教育学校のサイエンスカフェにて正五角形と三角比の関係についての講座を開催しました。
内容は、折り紙で正五角形を折ってそれを数学的な観点で見てみるという感じです。
参加者は、18人で中学1年生から高校2年生まで幅広い学生の方が参加してくださいました。
参加者の皆さんに来てくれた理由を聞くと、「幾何学が好きだから」や「折り紙が好きだから」、「今回の講座の先生に興味があったから」という事でした。
講座の流れはこんな感じです↓
・挨拶
・講師紹介
・芳賀先生紹介
・正五角形を折ってみる
・数学的な観点でみる
・TFOで遊ぶ
正五角形の折り方を数学的に検証しました。

【講座中の様子】
・挨拶
挨拶をして、参加者の皆さんが一人づつ自己紹介と講座に来てくれた理由を話してくれました。
・講師紹介
並木中等教育学校の吉村先生が講師として私たちを紹介してくれました。
・芳賀先生紹介
筑波大学でサイエンスキッズという子供向けの科学教室をやっていた芳賀先生を紙芝居で紹介しました。「オリガミクス」の考案者です。皆さんとても熱心な様子でうなずきながら聞いてくれました。
*芳賀先生本人にサイエンスキッズの真似をしてもいいかと許可をいただいたうえでイベントを開催しています。

・正五角形を折ってみる
始めの10分は、自分達で考えて正五角形を折ってみるという事で何枚か折り紙を渡して自由に折ってもらうことをしました。
いい線行っている人もいましたが、難しいようでなかなか思いつかない人が多い印象でした。
正五角形の折り方は何パターンかあるのですが、始めの10分が終わった後に1パターン一緒にやりました。




正五角形の折り方は芳賀和夫博士の著書「おりがみで楽しむ幾何学図形」や「オリガミクス1」に載っています。
・数学的な観点でみる
ここからは、変数、ルート、三角比を知っていた方がより分かりやすいと思います。ただ、ここはさほど難しく考えずになんとなくイメージを掴めればOKです。
今回、参加者の皆さんと一緒にやった折り方の工程で真ん中の印から2mmほど上にずらして折るという工程がありました。
その事について何故この工程が必要かを数学的にみるという事をしました。


何故2mmずらすのかについて説明したいのですが、先に正五角形という図形について復習します。
正五角形が成り立つ条件としては五角形である事、辺が全て同じ長さである事です。他にも角度などの特徴があります。

上の右側の辺と一番下の辺の延長線の交点のところに36°になる角があります。(半分にすると18°になります)
ここ重要なので覚えていてください↑
では、先程の工程で2mmずらさないで折るとどうなるかについて説明します。

2mmずらさずに折った場合、①の直角三角形の底辺と高さの比が1:3になります。
そうなると、①の一番鋭い角の角度が18.4°になります。
もし2mmずらさずに折った場合、肉眼で確認しても歪んでいて正五角形になっていないことがわかります。
つまり、①の一番鋭い角が18.4°では正五角形にならないという事です。
正五角形にするためには、①の一番鋭い角を18°にする必要があります。
そうすると何mmずらせば良いのかが問題になります。
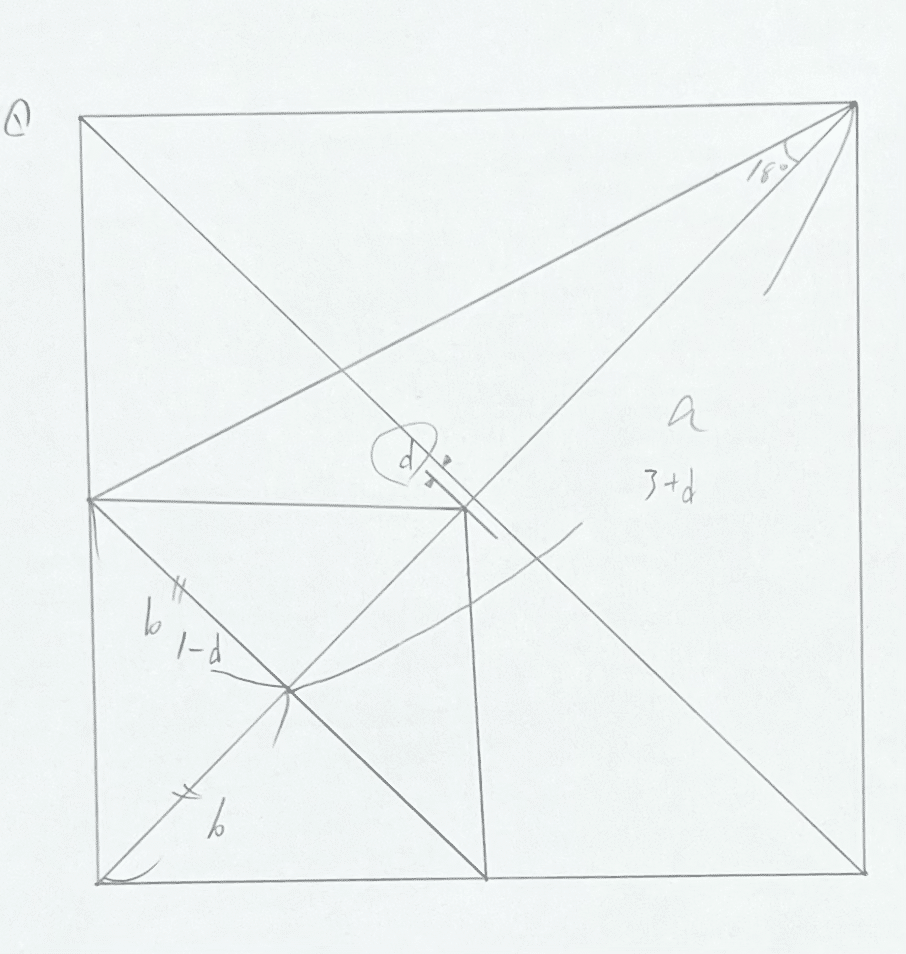
ちなみにこれは計算することができます。
tan18°=0.3249です。
150mm×150mmの折り紙の場合、aの長さが159mm、bの長さが53mmになります。
tan18°にするためにdmmずらすとします。
これを式に当てはめると

こうなります。
つまり、肉眼で誤差がわからない程度の正五角形にするためには、1.1mm程ずらす必要があります。
1mm強ずらせば良いという解釈でOKです。
ガッツリ解説してしまった😅
並木中等で解説した時には少し難しいという声もありましたが、興味深いと言った人もいました。
・TFOで遊ぶ
TFOを作って飛ばして遊びました。

最後に皆さんでTFOをより遠くに飛ばす方法を模索しました。
投げる力を変えてみたり、持ち方を変えてみたり色々な方法を試しました。
感想
今回のサイエンスカフェに参加してくれた人たちは、積極的に創意工夫をしていて素晴らしいと思いました。
私も練習してきた通りに緊張せずに喋る事ができてよかったです。
ただ、私が一方的に喋ってしまった時があった為、つぎは参加者の皆さんにも喋る時間を作るなどして改善できたら良いなと思いました。
今回は、サイエンスカフェに呼んでいただきありがとうございます。私も楽しかったです。


