
物理数学演習「微分方程式への応用」補足資料
横浜国立大学 理工学部 物理工学教育プログラムで2024年10月から開講している物理数学演習の「微分方程式への応用」の補足資料です.
教科書でも様々な例が扱われていますが,特に波動方程式を中心にFourier変換やデルタ関数を使うと便利な場面を紹介し,問題を実際に解くときに留数定理が有効であることを説明します.
公開:2025年1月20日
加筆:2025年1月20日14時
1次元波動方程式:特にMaxwellの方程式から電磁波について導出
まずは外力(外場)がない場合の1次元の波動方程式(波が従う運動方程式)
$$
\frac{\partial^2u}{\partial t^2} = c^2\frac{\partial^2u}{\partial x^2}
$$
を考える.$${t}$$は時刻,$${x}$$は位置であり,$${u}$$はそれらに依存する波の振幅である($${u(x,t)}$$).単純に一方向に伝播する水面の波や音波,電磁波などが従う運動方程式がこのような微分方程式となる.$${u(x,t)}$$はそれぞれ,波高,音圧,電場や磁場に対応する.$${c}$$はそれぞれの伝搬の速さである.

例えば,真空中の電磁波であればMaxwellの方程式のうち
$$
\bm{\nabla}\times\bm{E}=-\frac{\partial \bm{B}}{\partial t} \\
\frac{1}{\mu_0} \bm{\nabla}\times \bm{B} = \varepsilon_0 \frac{\partial \bm{E}}{\partial t}
$$
から波動方程式が以下の要領で得られる.第1式はFaradayの法則,第2式はAmpèreの法則を表わしており,$${\bm{E}}$$と$${\bm{B}}$$はそれぞれ電場と磁束密度,$${\varepsilon_0}$$と$${\mu_0}$$はそれぞれ真空の誘電率と透磁率である.

いま,電場と磁束密度が$${x}$$軸に沿ってのみ変動する($${x}$$軸に沿って伝播する)と仮定し,$${\bm{E}(x,t)}$$と$${\bm{B}(x,t)}$$のように,位置$${x}$$と時刻$${t}$$にのみ依存するとする.上記のMaxwellの方程式について,第1式の回転($${\bm{\nabla}\times}$$)をとり,第2式を代入すれば,
$$
-\varepsilon_0\mu_0 \frac{\partial^2\bm{E}}{\partial t^2}
=\bm{\nabla}\times(\bm{\nabla}\times\bm{E})
= \bm{\nabla}(\bm{\nabla}\cdot\bm{E})-\bm{\nabla}^2\bm{E}
= - \frac{\partial^2}{\partial x^2} \begin{pmatrix} 0 \\ E_y \\ E_z \end{pmatrix}
$$
が得られる.$${E_x}$$については時間に依存しない値(静電場)しか許されないことが分かる.一方,$${E_y}$$と$${E_z}$$は
$$
\frac{\partial^2E_y}{\partial t^2} = \frac{1}{\varepsilon_0\mu_0}\frac{\partial^2E_y}{\partial x^2} \\
\frac{\partial^2E_z}{\partial t^2} = \frac{1}{\varepsilon_0\mu_0}\frac{\partial^2E_z}{\partial x^2}
$$
のように,どちらも同じ形の波動方程式に従うことが分かる.後で見ていくように,$${c=1/\sqrt{\varepsilon_0\mu_0}}$$が電磁波の伝搬の速さ(真空中の光速)に対応する.これらの波動方程式によって$${E_{y,z}(x,t)}$$が決定され,磁束密度は上記Maxwellの方程式の第1式から
$$
\frac{\partial B_y}{\partial t} = \frac{\partial E_z}{\partial x} \\
\frac{\partial B_z}{\partial t} = - \frac{\partial E_y}{\partial x}
$$
と決定される.Maxwellの方程式の第2式の回転をとって第1式を代入すれば,磁束密度に対する波動方程式を得られ,それによって電磁波を記述してもよい.
1次元波動方程式の解:特に真空中の電磁波について
改めて1次元波動方程式として
$$
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2}
$$
を扱い,その解について考えていく.上の電磁波の例では,$${u(x,t)}$$は$${E_y(x,t)}$$もしくは$${E_z(x,t)}$$($${B_z(x,t)}$$や$${B_y(x,t)}$$でもよい),$${c=1/\sqrt{\varepsilon_0\mu_0}}$$である.
教科書にあるように,$${u(x,t)}$$は右向き($${x}$$軸正方向)に伝播する波$${\psi(x-ct)}$$と左向き($${x}$$軸負方向)に伝播する波$${\phi(x-ct)}$$の重ね合わせ
$$
u(x,t) = \psi(x-ct) + \phi(x+ct)
$$
で一般に表わされる.上記の波動方程式に代入すれば,確かに解になっていることが分かる.

右向きに進む波$${\psi(x-ct)}$$であれば,上図のように,速さ$${c}$$で波形が保たれたまま右向きに伝播していく.それは,時間$${t}$$だけ経過すれば,距離$${ct}$$だけ平行移動した位置に同じ波形として現われるからである.もしくは,ある地点$${x_0}$$での振幅$${\psi(x_0)}$$を考えれば,その振幅を持つ位置は$${x - ct = x_0}$$,つまり$${x = x_0 + ct}$$で決定されるため,その振幅が右向きに速さ$${c}$$で伝播すると考えてもよい.左向きの伝播については,符号が逆になるだけである.
さて,関数$${\psi}$$や$${\phi}$$は任意の関数である(ただし,$${u}$$が電場や磁束密度などの物理量を表わすのであれば,実関数と考えなければならない).いま,それらのFourier変換
$$
\psi(x-ct) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \varPsi(k) \mathrm{e}^{\mathrm{i}k(x-ct)} \mathrm{d}k \\
\phi(x+ct) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \varPhi(k) \mathrm{e}^{\mathrm{i}k(x+ct)} \mathrm{d}k
$$
を考える(一般に周期関数ではないので,Fourier級数展開ではなくFourier変換をする).これを
$$
\psi(x-ct) = \frac{1}{2\pi} \int_{0}^{\infty} \left[ \varPsi(k) \mathrm{e}^{\mathrm{i}k(x-ct)} + \varPsi(-k) \mathrm{e}^{-\mathrm{i}k(x-ct)} \right] \mathrm{d}k \\
\phi(x+ct) = \frac{1}{2\pi} \int_{0}^{\infty} \left[ \varPhi(k) \mathrm{e}^{\mathrm{i}k(x+ct)} + \varPhi(-k) \mathrm{e}^{-\mathrm{i}k(x+ct)} \right] \mathrm{d}k
$$
と書き直す.関数$${\psi}$$や$${\phi}$$が実関数であれば,$${\varPsi(-k) = \varPsi(k)^*}$$および$${\varPhi(-k) = \varPhi(k)^*}$$でなければならない.よって,
$$
\psi(x-ct) = \frac{1}{2\pi} \int_{0}^{\infty} \varPsi(k) \mathrm{e}^{\mathrm{i}k(x-ct)} \mathrm{d}k + \mathrm{c.c.}\\
\phi(x+ct) = \frac{1}{2\pi} \int_{0}^{\infty} \varPhi(k)^* \mathrm{e}^{-\mathrm{i}k(x+ct)} \mathrm{d}k + \mathrm{c.c.}
$$
と書くことができる.ここで,$${\mathrm{c.c.}}$$はその前の項の複素共役(complex conjugate)という意味である.第2式について$${\varPhi(k)^* \mathrm{e}^{-\mathrm{i}k(x+ct)}}$$の項をとってきた理由は,物理学において時間的な振動を$${\mathrm{e}^{-\mathrm{i}ckt}}$$という複素平面における位相回転を負の方向にとるという慣習からであり,数学的にはどちらをとってもよい.
ある$${k}$$の成分だけみれば,
$$
\varPsi(k) \mathrm{e}^{\mathrm{i}k(x-ct)} + \mathrm{c.c.}
= 2 |\varPsi(k)| \cos[k(x-ct)+\mathrm{arg\varPsi(k)}] \\
\varPhi(k)^* \mathrm{e}^{-\mathrm{i}k(x+ct)} + \mathrm{c.c.}
= 2 |\varPhi(k)| \cos[k(x+ct)+\mathrm{arg\varPhi(k)}]
$$
これらは最大振幅$${2|\varPsi(k)|}$$や$${2|\varPhi(k)|}$$の単なる余弦波(平面波)である.このような余弦波(や正弦波)の重ね合わせ(様々な$${k}$$の成分の積分)で波を表わすというのが,Fourier変換による解析の1つの考え方である.
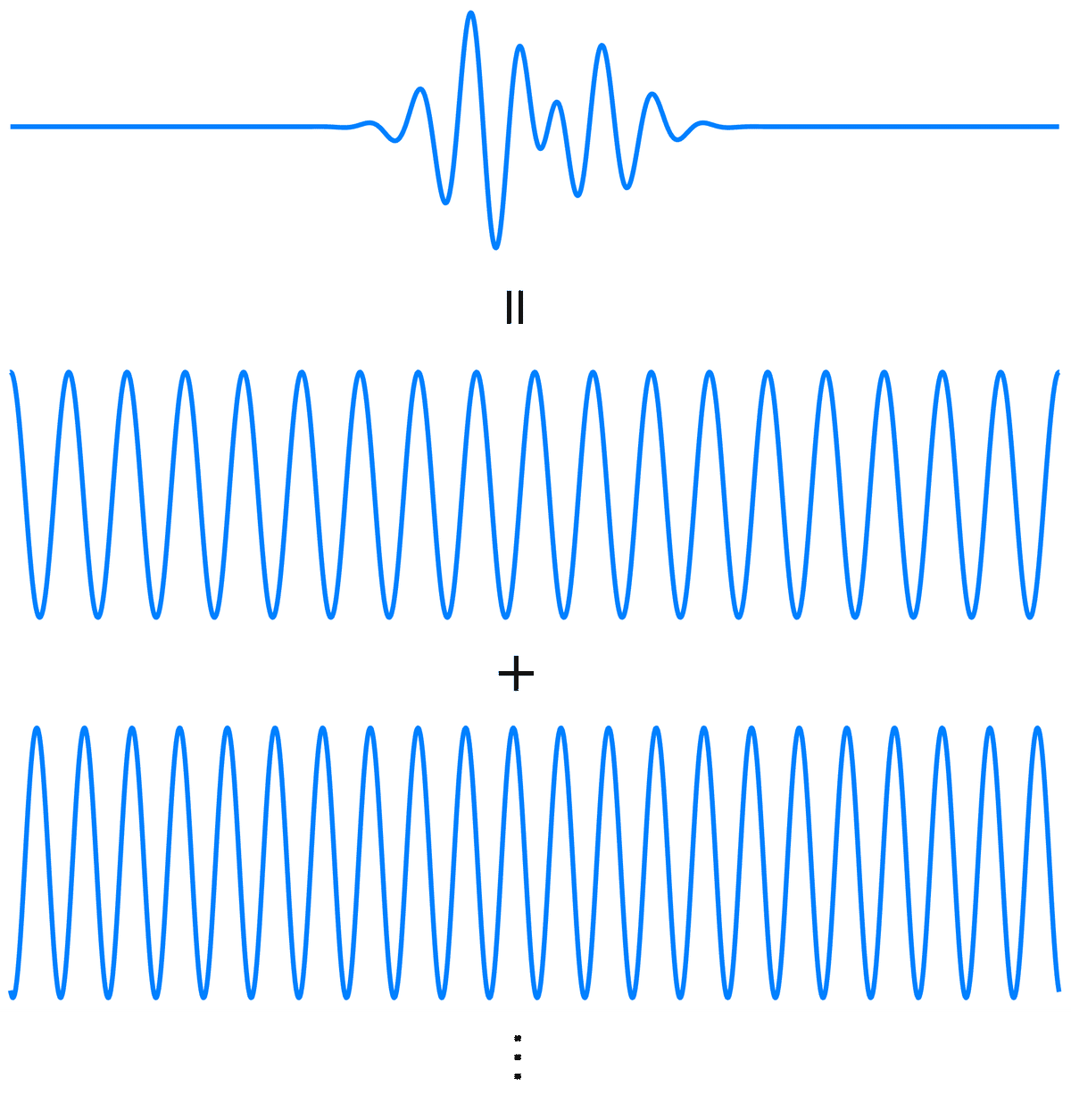
$${\cos[k(x \pm ct)]}$$や$${\sin[k(x \pm ct)]}$$,$${\mathrm{e}^{\mathrm{i}k(x \pm ct)}}$$に現われる$${k}$$は波数とよばれ,波長$${\lambda}$$と$${k = 2\pi/\lambda}$$の関係がある.つまり,長さの逆の次元をもち,単位長さあたりに含まれる節や腹の数(を$${\pi}$$で割ったもの)を意味する.また,$${ck}$$は角振動数(角周波数)であり,振動数は$${\nu = ck/(2\pi) = c/\lambda}$$,周期は$${T = 1/\nu = \lambda/c}$$で与えられる.

上記は余弦波などを波数$${k}$$で特徴づける(あらゆる波は様々な波数の余弦波の重ね合わせで展開できる)という発想だが,波数の代わりに角振動数$${\omega = ck}$$で特徴づけることもできる.つまり,積分変数を$${\omega=ck}$$と変換して
$$
\psi(x-ct) = \frac{1}{2\pi c} \int_{0}^{\infty} \varPsi(\omega/c) \mathrm{e}^{-\mathrm{i}\omega(t-x/c)} \mathrm{d}\omega + \mathrm{c.c.}\\
\phi(x+ct) = \frac{1}{2\pi c} \int_{0}^{\infty} \varPhi(\omega/c)^* \mathrm{e}^{-\mathrm{i}\omega(t+x/c)} \mathrm{d}\omega + \mathrm{c.c.}
$$
と書き直すことができる.それぞれの振動成分$${\mathrm{e}^{-\mathrm{i}\omega(t \mp x/c)}}$$,$${\cos[\omega(t \mp x/c)]}$$や$${\sin[\omega(t \mp x/c)]}$$は角振動数$${\omega}$$で特徴づけられ,その波の波数は$${\omega/c}$$,波長は$${\lambda = 2\pi c/ \omega}$$で与えられる.波を様々な角振動数の余弦波などの重ね合わせと考える発想である.
波数$${k}$$と角振動数$${\omega}$$(もしくは振動数$${\nu=\omega/(2\pi)}$$)のどちらに基づいて解析してもよい.ただし,ポテンシャルや媒質が位置$${x}$$に依存して,運動方程式が$${x}$$には依存するが時刻$${t}$$には依存しない(同じ形をしている)場合,例えば速さ$${c(x)}$$が位置によって異なる場合
$$
\frac{\partial^2u}{\partial t^2} = c(x)^2\frac{\partial^2u}{\partial x^2}
$$
を考えてみる(電磁波でいえば屈折率が場所に依存する場合).この場合,角振動数$${\omega}$$は保存量となり(系が時間発展しても,ある$${\omega}$$の成分が異なる$${\omega}$$に変化したりしない;混じり合ったりしない;線形な重ね合わせがずっと成り立つ),様々な$${\omega}$$の重ね合わせと考える方が見通しがよくなる.一方,波数$${k}$$は保存量ではなくなってしまう.もちろん逆に,時間的に振動する外力(例えば電磁波)で空間的に均一に系を駆動するなど,運動方程式が位置に依存せず時間に依存するなら,様々な$${k}$$の重ね合わせと考えた方がよい.また,量子力学的には$${\hbar\omega}$$が量子1個のエネルギーに対応するので,$${\omega}$$で考えた方がエネルギー保存則などの見通しがよくなる.

また,テラヘルツ以下の振動数の電磁波であれば,電場の時間的な波形$${u(x,t)}$$を検出しやすいが,それよりも高い振動数の電磁波(赤外光や可視光など)であれば,回折格子やプリズムを使って分光する(スペクトルをとる)ことが多い.

これは検出器の方に伝播してきた電磁波の成分$${\varPsi(\omega/c)}$$の強度$${{|\varPsi(\omega/c)}|^2}$$を振動数$${\nu=\omega/(2\pi)}$$ごとに検出することに相当する(スペクトルとしてプロットするときは振動数$${\nu=\omega/(2\pi)}$$の代わりに波長$${\lambda=c/\nu}$$,1光子あたりのエネルギー$${\hbar\omega}$$や$${1/\lambda}$$(これも波数とよばれる)で表示したりもする).このように実験データを扱う際にも,信号がFourier変換されたものを実際には検出している場合がある.
強制振動のある1次元波動方程式
次に,1次元波動方程式に外力$${f(x,t)}$$と減衰レート$${\kappa}$$の減衰項を付け加えた
$$
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} - 2\kappa\frac{\partial u}{\partial t} + f(x,t)
$$
を考える.下記の演習問題で考えるように,例えば,$${x=0}$$に光源(面光源)がある場合に発生する電磁波を記述する方程式である.真空中であれば,減衰レートは最後に$${\kappa\to0}$$の極限をとればよい.

このように外力が一般にある場合,たとえ$${\kappa\to0}$$のであっても,前節のように$${\psi(x-ct)}$$と$${\phi(x+ct)}$$の重ね合わせとして書くことは必ずしもできない.ここでは,振幅$${u(x,t)}$$を位置$${x}$$についてFourier変換した$${U(k,t)}$$を導入し,波数$${k}$$の成分ごとに考えていく.すなわち,$${u(x,t)}$$を$${U(k,t)}$$で表わした(逆Fourier変換した)
$$
u(x,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} U(k,t) \mathrm{e}^{\mathrm{i}kx} \mathrm{d}k
$$
を考える.これの空間微分は
$$
\frac{\partial}{\partial x}u(x,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} (\mathrm{i}k) U(k,t) \mathrm{e}^{\mathrm{i}kx} \mathrm{d}k \\
\frac{\partial^2}{\partial x^x}u(x,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} (-k^2) U(k,t) \mathrm{e}^{\mathrm{i}kx} \mathrm{d}k
$$
となる.Fourier変換すると$${(\partial/\partial x) \to \mathrm{i}k}$$に置き換えられる.これを踏まえて,上記の$${u(x,t)}$$の表式を上記の運動方程式に代入すると
$$
\frac{1}{2\pi}\int_{-\infty}^{\infty} \left( \frac{\partial^2}{\partial t^2} + c^2k^2 + 2\kappa\frac{\partial}{\partial t} \right) U(k,t) \mathrm{e}^{\mathrm{i}kx} \mathrm{d}k = f(x,t)
$$
が得られる.両辺に$${\mathrm{e}^{-\mathrm{i}kx}}$$を掛けて$${x}$$に付いて$${(-\infty,\infty)}$$の範囲で積分すれば,
$$
\frac{1}{2\pi}\int_{-\infty}^{\infty} \mathrm{e}^{\mathrm{i}(k'-k)x} \mathrm{d}x = \delta(k'-k)
$$
がデルタ関数になることを使うと
$$
\left( \frac{\partial^2}{\partial t^2} + c^2k^2 + 2\kappa\frac{\partial}{\partial t} \right) U(k,t) = \int_{-\infty}^{\infty} f(x,t) \mathrm{e}^{-\mathrm{i}kx} \mathrm{d}x = F(k,t)
$$
が得られる.右辺の$${F(k,t)}$$は外力$${f(x,t)}$$のFourier変換である.このように,波数$${k}$$の成分ごとに減衰振り子の強制振動の問題に帰着する.各振り子の共鳴振動数は$${\nu_k = ck/(2\pi)=c/\lambda_k}$$であり,波数に比例して振り子の振動数は高くなる.$${U(k,t)}$$をすべて求めれば,逆Fourier変換で$${u(x,t)}$$を得ることができる.

減衰振動子の強制振動
前節に現われた外力$${F(k,t)}$$によって強制振動される減衰振り子の運動方程式
$$
\left( \frac{\partial^2}{\partial t^2} + \omega_k{}^2 + 2\kappa\frac{\partial}{\partial t} \right) U(k,t) = F(k,t)
$$
の解を求める.$${k}$$ごとに振幅$${U(k,t)}$$を求めればよい.教科書では外力が周期的と仮定したのでFourier級数展開をしたが,ここでは一般の場合を考え,時刻$${t}$$についてもFourier変換した
$$
\mathcal{U}(k,\omega) = \int_{-\infty}^{\infty} U(k,t) \mathrm{e}^{\mathrm{i}\omega t} \mathrm{d}t \\
\mathcal{F}(k,\omega) = \int_{-\infty}^{\infty} F(k,t) \mathrm{e}^{\mathrm{i}\omega t} \mathrm{d}t
$$
を導入する.ここで,$${\mathrm{e}^{\mathrm{i}\omega t}}$$の肩の符号が位置$${x}$$についてのFourier変換と逆なのは物理学の慣習によるものであり,数学的にはどちらでもよい.とにかく,上記の運動方程式の両辺に$${\mathrm{e}^{\mathrm{i}\omega t}}$$を掛けて$${t}$$に付いて$${(-\infty,\infty)}$$の範囲で積分すれば(部分積分を使ってもよいし,前節のようにそれぞれの逆Fourier変換の式を代入してもよい)
$$
\left( -\omega^2 + \omega_k{}^2 - \mathrm{i}2\kappa\omega \right) \mathcal{U}(k,\omega) = \mathcal{F}(k,\omega)
$$
$$
\mathcal{U}(k,\omega) = \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega}
$$
が得られる(時間微分$${\partial/\partial t}$$が$${-\mathrm{i}\omega}$$に置き換わる).つまり,時間微分が(波動方程式では空間微分も)含まれる運動方程式(微分方程式)であっても,外力を時間(や空間で)Fourier変換すれば,求めたい振幅のFourier変換$${\mathcal{U}(k,\omega)}$$が簡単に得られる.これを逆Fourier変換すれば,本来求めたかった
$$
U(k,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} \mathrm{e}^{-\mathrm{i}\omega t} \mathrm{d}\omega \\
u(x,t) = \frac{1}{(2\pi)^2}\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} \mathrm{e}^{\mathrm{i}(kx-\omega t)} \mathrm{d}\omega \mathrm{d}k
$$
が得られる.これらの評価には,$${\mathcal{F}(k,\omega)}$$が正則な関数であるなら,留数定理が効力を発揮する(下記の演習問題).
演習問題
問題11-1
上で扱った減衰振動子の運動方程式
$$
\left( \frac{\partial^2}{\partial t^2} + \omega_k{}^2 + 2\kappa\frac{\partial}{\partial t} \right) U(k,t) = F(k,t)
$$
について,上記のように振幅と外力を時間についてFourier変換($${U(k,t)\to\mathcal{U}(k,\omega)}$$, $${F(k,t)\to\mathcal{F}(k,\omega)}$$)することで
$$
\left( -\omega^2 + \omega_k{}^2 - \mathrm{i}2\kappa\omega \right) \mathcal{U}(k,\omega) = \mathcal{F}(k,\omega)
$$
となることを示せ.
問題11-2
位置$${x=0}$$に光源(面光源)があると想定し,外力が$${f(x,t) = \delta(x) \eta(t)}$$と表わされるとする.つまり,時間についてのFourier変換は単に
$$
F(k,t) = \int_{-\infty}^{\infty} f(x,t) \mathrm{e}^{-\mathrm{i}kx} \mathrm{d}x = \eta(t)
$$
となる.時間波形として
(1) $${\eta(t) = \begin{cases} \eta_0 \mathrm{e}^{-t/\tau} \sin(\omega_{\mathrm{e}}t) & t > 0 \\ 0 & t < 0\end{cases}}$$
(2)$${\eta(t) = \eta_0 \mathrm{e}^{-t^2/\tau^2} \cos(\omega_{\mathrm{e}}t)}$$
の2パターンを考え,
$$
\mathcal{F}(k,\omega) = \int_{-\infty}^{\infty} F(k,t) \mathrm{e}^{\mathrm{i}\omega t} \mathrm{d}t
$$
を求めることで,
$$
U(k,t) = \frac{1}{2\pi}\int_{-\infty}^{\infty} \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} \mathrm{e}^{-\mathrm{i}\omega t} \mathrm{d}\omega
$$
を評価せよ.
Green関数
前節が上記の微分方程式の1つの解き方ではあるが,複素関数の積分で紹介したとおり,Green関数を使っても解を定式化することができる.まず,方程式
$$
\left( \frac{\partial^2}{\partial t^2} + \omega_k{}^2 + 2\kappa\frac{\partial}{\partial t} \right) G_k(t) = \delta(t)
$$
を満たすGreen関数$${G_k(t)}$$を考える.これを用いると,振幅$${U(k,t)}$$は外場$${F(k,t)}$$から
$$
U(k,t) = \int_{-\infty}^{\infty} G_k(t-t') F(k,t') \mathrm{d}t'
$$
と決定することができる.それは,この表式を上記の運動方程式に代入すれば,
$$
\left( \frac{\partial^2}{\partial t^2} + \omega_k{}^2 + 2\kappa\frac{\partial}{\partial t} \right) U(k,t)
= \int_{-\infty}^{\infty} \delta(t-t') F(k,t') \mathrm{d}t'
= F(k,t)
$$
となり,確かに運動方程式を満たすことが分かる.一方,Green関数は時間についてFourier変換することで
$$
\mathcal{G}_k(\omega)=\int_{-\infty}^{\infty} G_k(t) \mathrm{e}^{\mathrm{i}\omega t} \mathrm{d}t
= \frac{1}{\omega_k{}^2 - \omega^2 - \mathrm{i}2\kappa\omega}
$$
$$
G_k(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\mathrm{e}^{-\mathrm{i}\omega t}}{\omega_k{}^2 - \omega^2 - \mathrm{i}2\kappa\omega} \mathrm{d}\omega
$$
と求めることができる.この表式をそのまま代入すると振幅は
$$
U(k,t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \int_{-\infty}^{\infty} \frac{\mathrm{e}^{-\mathrm{i}\omega(t-t')}F(k,t') }{\omega_k{}^2 - \omega^2 - \mathrm{i}2\kappa\omega} \mathrm{d}\omega \mathrm{d}t' \\
= \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\mathrm{e}^{-\mathrm{i}\omega t} \mathcal{F}(k,\omega) }{\omega_k{}^2 - \omega^2 - \mathrm{i}2\kappa\omega} \mathrm{d}\omega
$$
となり,上と同じ結果が得られる.
さて,あえてGreen関数を導入しなくても,前節のように運動方程式全体をFourier変換すれば同じ結果が得られるわけだが,Green関数を導入した方が見通しがよくなる場合が存在する.
1つは分光してスペクトルとして信号を検出する場合である.上記の通り,赤外光や可視光は電場の時間的なダイナミクスではなく,時間についてFourier変換されたスペクトル(振動数成分の強度)として検出される.いまの運動方程式でいえば,
$$
\mathcal{U}(k,\omega) = \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega}
$$
なり,検出器の位置を$${x_0}$$として実空間に逆Fourier変換した
$$
\mathscr{U}(x_0,\omega) = \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{ \mathcal{F}(k,\omega) }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} \mathrm{e}^{\mathrm{i}kx_0} \mathrm{d}k
$$
の強度である$${|\mathcal{U}(k,\omega)|^2}$$や$${|\mathscr{U}(x_0,\omega)|^2}$$が検出される.これらももちろん外力のFourier変換$${\mathcal{F}(k,\omega)}$$で決定されるものだが,もし関心のある物理量が透過係数(その絶対値2乗が透過率)であるなら,それは
$$
\frac{\mathcal{U}(k,\omega)}{\mathcal{F}(k,\omega) } = \frac{ 1 }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} = \mathcal{G}_k(\omega)
$$
$$
\frac{\mathscr{U}(x_0,\omega)}{ \mathcal{F}(k,\omega) } = \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{ \mathrm{e}^{\mathrm{i}kx_0} }{\omega_k{}^2 -\omega^2 - \mathrm{i}2\kappa\omega} \mathrm{d}k
= \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathcal{G}_k(\omega) \mathrm{e}^{\mathrm{i}kx_0} \mathrm{d}k
$$
となる.ただし,第2式については,上記の演習問題のように外力(光源)が位置的にデルタ関数$${\delta(x)}$$で書かれるとして,そのFourier変換$${\mathcal{F}(k,\omega)}$$が波数$${k}$$に依存しないとした.このように透過係数という系に固有の性質(プローブのための外力に依存しない)については,Green関数という系の応答関数が肝心となる.
その他にGreen関数が現われる例としては,物質の電気感受率や誘電率であり,その結果として物質中の電磁波の波動方程式自体が変化するというものである.

ここでは,複素関数の積分で扱った上のような電荷を持つ振り子(振動子)が敷き詰められているというモデルで物質が記述される場合を考える.3年秋学期の物性物理学の講義で扱われる誘電体(絶縁体)中の光学フォノンがそのようなモデルで記述される.
ある位置$${x}$$の振動子が電場$${E(t)}$$によって揺らされることで(振幅が誘起されることで),振動する分極$${P(x,t)}$$が誘起される.導出は割愛するが,共鳴角振動数$${\omega_0}$$と減衰レート$${\gamma}$$でのGreen関数
$$
G(t)= \frac{1}{2\pi} \int_{-\infty}^{\infty} \mathcal{G}(\omega) \mathrm{e}^{-\mathrm{i}\omega t} \mathrm{d}\omega \\
\mathcal{G}(\omega) = \frac{1}{\omega_0{}^2 - \omega^2 - \mathrm{i}2\gamma\omega}
$$
を用いて分極は
$$
P(x,t) = \varepsilon_0 f \omega_{\mathrm{p}}{}^2\int_{-\infty}^{\infty}G(t-t')E(x,t') \mathrm{d}t' \\
\mathscr{P}(x,\omega) = \varepsilon_0 f \omega_{\mathrm{p}}{}^2 \mathcal{G}(\omega)\mathscr{E}(x,\omega)
$$
と表わされる.$${f}$$は振動子強度,$${\omega_{\mathrm{p}}}$$はプラズマ角振動数とよばれるものである.教科書で扱ったように,たたみ込み積分のFourier変換はFourier変換同士の積となる.電気感受率を$${\chi(\omega) = f \omega_{\mathrm{p}}{}^2 \mathcal{G}(\omega)}$$と書くことにすれば,分極のFourier変換は$${\mathscr{P}(x,\omega) = \varepsilon_0\chi(\omega)\mathscr{E}(x,\omega)}$$と表わされ,電束密度のFourier変換は
$$
\mathscr{D}(x,\omega)=\varepsilon_0\mathscr{E}(x,\omega) + \mathscr{P}(x,\omega)=\varepsilon_0\varepsilon_{\mathrm{r}}(\omega)\mathscr{E}(x,\omega)
$$
と表わされる.比誘電率は
$$
\varepsilon_{\mathrm{r}}(\omega) = 1 + \chi(\omega) = 1 + f \omega_{\mathrm{p}}{}^2 \mathcal{G}(\omega)
$$
と角振動数$${\omega}$$に依存し,Green関数のFourier変換で表わされることになる.このような物質中での電磁波の波動方程式を考えると,Maxwellの方程式は
$$
\bm{\nabla}\times\bm{E}(\bm{r},t)=-\frac{\partial}{\partial t} \bm{B}(\bm{r},t) \\
\frac{1}{\mu_0} \bm{\nabla}\times \bm{B}(\bm{r},t) = \varepsilon_0 \frac{\partial}{\partial t} \int_{-\infty}^{\infty} \epsilon_{\mathrm{r}}(t-t') \bm{E}(\bm{r},t')
$$
となる($${\epsilon_{\mathrm{r}}(t)}$$は比誘電率$${\varepsilon_{\mathrm{r}}(\omega)}$$の逆Fourier変換).たたみ込み積分が現われてしまうので,全体を時間についてFourier変換した
$$
\bm{\nabla}\times\bm{\mathscr{E}}(\bm{r},\omega) = \mathrm{i}\omega\bm{\mathscr{B}}(\bm{r},\omega) \\
\frac{1}{\mu_0} \bm{\nabla}\times \bm{\mathscr{B}}(\bm{r},\omega) = - \mathrm{i} \varepsilon_0 \omega \varepsilon_{\mathrm{r}}(\omega) \bm{\mathscr{E}}(\bm{r},\omega)
$$
を扱うとすっきりする.これらから波動方程式は時間についてFourier変換した形で
$$
- \omega^2 \mathscr{U}(x,\omega) = \frac{1}{\varepsilon_{\mathrm{r}}(\omega) \varepsilon_0\mu_0}\frac{\partial^2}{\partial x^2} \mathscr{U}(x,\omega)
$$
と得られる(左辺の時間についての2階微分は$${-\omega^2}$$に置き換えられる).つまり,伝搬速度(正確には位相速度)が$${\omega}$$に依存して$${c/\sqrt{\varepsilon_{\mathrm{r}}(\omega)}}$$と変更される.このように,物質の比誘電率や電磁波の伝搬速度という物質の性質としてGreen関数がよく現われる.
演習問題
問題11-3
上記のGreen関数が$${\omega_0 > \gamma}$$の場合に
$$
G(\tau)= \frac{1}{2\pi} \int_{-\infty}^{\infty} \frac{\mathrm{e}^{-\mathrm{i}\omega\tau}}{\omega_0{}^2 - \omega^2 - \mathrm{i}2\gamma\omega} \mathrm{d}\omega = \begin{cases} \frac{\mathrm{i}}{2\tilde{\omega}_0} \mathrm{e}^{-\gamma\tau} \left( \mathrm{e}^{-\mathrm{i}\tilde{\omega}_0\tau}-\mathrm{e}^{\mathrm{i}\tilde{\omega}_0\tau} \right) & \tau \ge 0 \\ 0 & \tau < 0 \end{cases} \\
$$
となることを示せ.ただし,$${\tilde{\omega}_0 = \sqrt{\omega_0{}^2-\gamma^2}}$$である.これは振幅$${u(t)}$$が外力$${f(t)}$$に対して
$$
u(t) = \int_{-\infty}^t G(t-t') f(t') \mathrm{d}t' = \int_0^{\infty} G(\tau) f(t-\tau) \mathrm{d}\tau
$$
と表わされること,つまり,時刻$${t}$$での振幅$${u(t)}$$が$${t > t'}$$を満たす過去の時刻$${t'}$$での外力$${f(t')}$$によって決定される(未来の情報には影響されない)ことを意味する.これは因果律(causality)とよばれるものである.
境界条件のある波動方程式:電磁波の共振器
教科書では波動方程式に境界条件と振幅が最初にあるという初期条件を課して解を求めたが,ここでは振幅がゼロの初期条件を考え,その代わりに外力$${f(x,t)}$$が一般にあると想定し,波動方程式
$$
\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partial x^2} + f(x,t)
$$
に境界条件を課して解いていく.境界条件としては単純に位置$${x = 0, L}$$において振幅がゼロになる
$$
u(0,t) = u(L,t) = 0
$$
という条件を考え,$${0\le x \le L}$$での振幅を議論する.電磁波の場合,位置$${x = 0, L}$$に反射率$${R=1}$$の鏡があり,Maxwellの境界条件から電場がそれらの位置でゼロとなるような状況に相当する.以降で見られるように,電磁波の共振器の系に相当する.

まず,外力がない場合の一般解を考える.空間的に周期的ではないので,ここでもFourier変換を用いるが,複素指数関数ではなく余弦波と正弦波を用いた
$$
u(x,t) = \frac{1}{\pi} \int_0^{\infty} \left[ A(k,t) \cos(kx) + B(k,t) \sin(kx) \right] \mathrm{d}k
$$
を考える.境界条件を考えると
$$
u(0,t) = \frac{1}{\pi} \int_0^{\infty} A(k,t) \mathrm{d}k = 0
$$
より,$${A(k,t) = 0}$$となることが分かる.一方,
$$
u(L,t) = \frac{1}{\pi} \int_0^{\infty} B(k,t) \sin(kL) \mathrm{d}k = 0
$$
より,
$$
k = \frac{n\pi}{L} \quad (n = 1, 2, 3, \ldots)
$$
の波数でのみ成分を持つことが分かる.よって,デルタ関数を用いて
$$
B(k,t) = \sum_{n=1}^{\infty} \delta(k-n\pi/L) U_n(t)
$$
と書くことにすると,振幅は一般に
$$
u(x,t) = \frac{1}{\pi} \sum_{n=1}^{\infty} U_n(t) \sin(n\pi x/L)
$$
と表わされることが分かる.これを波動方程式に代入すれば
$$
\frac{1}{\pi} \sum_{n=1}^{\infty}\left[ \frac{\partial^2}{\partial t^2} + \left(\frac{n\pi c}{L}\right)^2 \right] U_n(t) \sin(n\pi x/L) = f(x,t)
$$
両辺に$${(2\pi/L)\sin(n\pi x/L)}$$を掛けて$${x}$$について$${[0,L]}$$の範囲で積分すれば,
$$
\left[ \frac{\partial^2}{\partial t^2} + \left(\frac{n\pi c}{L}\right)^2 \right] U_n(t) = F_n(t) = \frac{2\pi}{L}\int_{0}^{L} f(x,t) \sin(n\pi x/L) \mathrm{d}x
$$
が得られ,共鳴角振動数$${\omega_n = n\pi c/L}$$の振り子(振動子)の強制振動の問題に帰着する.それぞれのモードの振幅$${U_n(t)}$$は外力$${\sin(n\pi x/L)}$$の空間形状と時間的な振動によって決まり,波の振幅はそれらの重ね合わせ$${u(x,t) = \frac{1}{\pi} \sum_{n=1}^{\infty} U_n(t) \sin(n\pi x/L)}$$となる.
このように,基本振動の振動数は$${\nu_1 = \omega_1/(2\pi) = c/(2L)}$$のように波の速さ$${c}$$と長さ$${L}$$で決まり,その倍波$${\nu_n = n\nu_1 = nc/(2L)}$$が存在する(それぞれの波長は$${\lambda_n = c / \nu_n = 2L / n}$$)というのは,弦楽器の定在波でも共振器中の電磁波でも同じ方程式として記述される(ただし,電磁波の場合は外力は鏡を通じて入ってくる場合が多く,反射率$${R<1}$$の鏡を考え,$${x=0,L}$$に外力が発生すると考える必要がある).
