最適化ソルバー比較
数理最適化ソルバー
以下の表に各ソルバーの詳細な比較情報が示されています。この表には、各ソルバーのライセンスタイプ、性能、価格情報が含まれています。
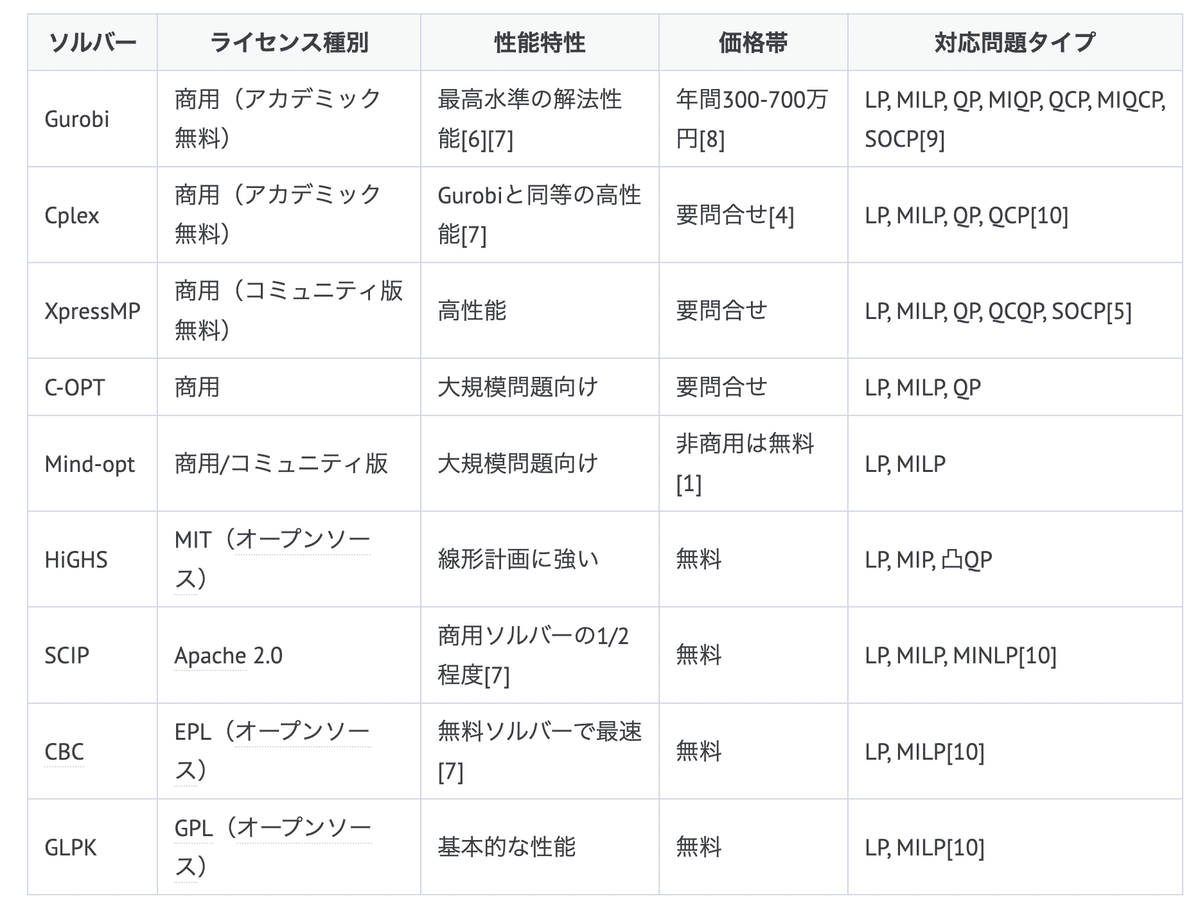
補足として、これらのソルバーは大きく商用とオープンソースの2つのカテゴリーに分類できます。商用ソルバーは高価ですが、一般的に最高レベルの性能を提供します。一方、オープンソースソルバーは無料で利用でき、多くの場合、十分な性能を発揮します。
追記:上でCBCが最速という元記事はGurobiの人で、2018年でした。今はCBCよりSCIPやHiGHSの方が速いです。
Citations:
[1] https://www.mindstudio.ai/pricing
[2] https://cran.r-project.org/web/packages/prioritizr/vignettes/gurobi_installation_guide.html
[3] https://www.reddit.com/r/opensource/comments/o4wf3g/which_license_is_best_for_noncommercial_purposes/
[4] https://www.ibm.com/products/ilog-cplex-optimization-studio/pricing
[5] https://www.fico.com/fico-xpress-optimization/docs/latest/installguide/dhtml/chapinst1.html
[6] https://www.gurobi.com/resources/beyond-speed-understanding-the-true-meaning-of-solver-performance/
[7] https://groups.google.com/g/pulp-or-discuss/c/b-d-Xjm7-Xw
[8] https://ampl.com/products/solvers/solvers-we-sell/gurobi/
[9] https://www.gurobi.com/solutions/gurobi-optimizer/
[10] https://inarizuuuushi.hatenablog.com/entry/2020/09/29/224552
主要な数理最適化問題の分類
LP (Linear Programming)
線形計画問題。目的関数と制約条件がすべて線形な最適化問題です[1]。
MILP (Mixed Integer Linear Programming)
混合整数線形計画問題。LPの変数の一部が整数値をとる必要がある問題です[2]。
QP (Quadratic Programming)
二次計画問題。目的関数が二次関数で、制約条件が線形な最適化問題です[3]。
QCQP (Quadratically Constrained Quadratic Program)
二次制約付き二次計画問題。目的関数と制約条件の両方が二次関数である最適化問題です[4]。
SOCP (Second-Order Cone Programming)
二次錐計画問題。制約条件に二次錐制約を含む最適化問題です[5]。
NLP (NonLinear Programming)
非線形計画問題。目的関数または制約条件の一部が非線形である最適化問題です[6]。
これらの問題は、一般的に LP → MILP/QP → SOCP → QCQP → NLP の順で難しくなります。特に、非凸なQCQPやNLPは、大域的最適解を求めることが計算的に困難なNP困難な問題となります[4]。
Citations:
[1] https://www.symestic.com/en-us/what-is/linear-programming-model-lp-modell
[2] https://www.mathworks.com/help/optim/ug/mixed-integer-linear-programming-algorithms.html
[3] https://www.mathworks.com/discovery/quadratic-programming.html
[4] https://en.wikipedia.org/wiki/Quadratically_constrained_quadratic_program
[5] https://www.cvxpy.org/examples/basic/socp.html
[6] https://en.wikipedia.org/wiki/Nonlinear_programming
[7] https://www.spiceworks.com/tech/it-strategy/articles/linear-programming/
[8] https://towardsdatascience.com/mixed-integer-linear-programming-formal-definition-and-solution-space-6b3286d54892?gi=014c30bb6e44
[9] https://en.wikipedia.org/wiki/Quadratic_programming
[10] https://www.princeton.edu/~aaa/Public/Teaching/ORF523/ORF523_Lec9.pdf
数理最適化以外のソルバー
数理最適化以外のソルバーもあります。以下にまとめます。

表を参照いただくと、メタヒューリスティクスやその他の最適化ソルバーの特徴が整理されています。
これらのソルバーは、厳密な数理最適化とは異なるアプローチで最適化を行います。特に、大規模な組合せ最適化問題や、厳密解を必要としない場合に有効です。
補足として、これらのソルバーは以下のような特徴があります:
メタヒューリスティクスベースのソルバーは、大規模問題でも現実的な時間で解を得られる利点があります[2]
これらのソルバーは、問題の性質や規模に応じて使い分けることが重要です[4]。
OptSeqとSCOPは、MOAI LabのCEOが開発したものなので、現場の要望に応じたカスタマイズが可能です。
Citations:
[1] https://ai.access-company.com/1/
[2] https://www.ipros.jp/cg2/最適化ソルバー/
[3] https://note.com/magemanager/n/n2e73e7f557fc
[4] https://www.chowagiken.co.jp/blog/mathematical_optimization
[5] https://www.nag-j.co.jp/naglib/optimization/solver-selection-guide.htm
[6] https://codeokiba.com/solver-combinatorial-optimization/
[7] https://www.ibm.com/jp-ja/optimization-solver
[8] https://note.com/mokazaka/n/nd22f2092ea51
[9] https://the-simple.jp/what-is-a-solver-introducing-types-of-solvers-and-how-to-use-them
[10] https://www.logopt.com/optseq/
[11] https://www.logopt.com/scop2/
[12] https://www.logopt.com/english/solutions/scop/
[13] https://www.solver.com/pricing-excel-product-software-and-support
[14] https://support.microsoft.com/en-us/office/define-and-solve-a-problem-by-using-solver-5d1a388f-079d-43ac-a7eb-f63e45925040
[15] https://en.wikipedia.org/wiki/OR-Tools
[16] https://github.com/google/or-tools
[17] https://www.nuget.org/packages/Google.OrTools/
[18] https://developers.google.com/optimization/introduction
[19] https://reference.wolfram.com/language/workflow/GetALicenseForMOSEK.html
[20] https://www.solver.com/mosek-solver-engine-product
[21] https://www.mosek.com/sales/commercial-pricing/
[22] https://www.mosek.com/products/mosek/
[23] https://doc.sagemath.org/html/en/reference/spkg/cvxopt.html
[24] https://scaron.info/blog/linear-programming-in-python-with-cvxopt.html
[25] https://cvxopt.org
[26] https://cvxopt.org/userguide/modeling.html
[27] https://en.wikibooks.org/wiki/GLPK/License
[28] https://www.gurobi.com/resources/open-source-mixed-integer-and-linear-programming-solvers/
[29] https://savannah.gnu.org/projects/glpk
[30] https://www.geeksforgeeks.org/what-is-tabu-search/
[31] https://en.wikipedia.org/wiki/Tabu_search
[32] https://www.mathworks.com/help/gads/genetic-algorithm.html
[33] https://en.wikipedia.org/wiki/Genetic_Algorithm
[34] https://en.wikipedia.org/wiki/Simulated_annealing