Deeplearningとは?畳み込み層、プーリング層、全結合層を解説!
Deep leaningとは
「良い関数を見つけて使うこと」です。
でも物体認識とかで「猫」とか「犬」の画像は関数とは違うんじゃないか??
と思う方もいるかと思います。しかし、そもそも画像データとはR(Red)G(GreenB(Brue)の三原色の0~255階調で表現されます。
そのため画像が縦100ピクセル、横100ピクセルの合計10,000ピクセルの場合には、10,000✖︎3(階調)=30,000で表現されるわけです。
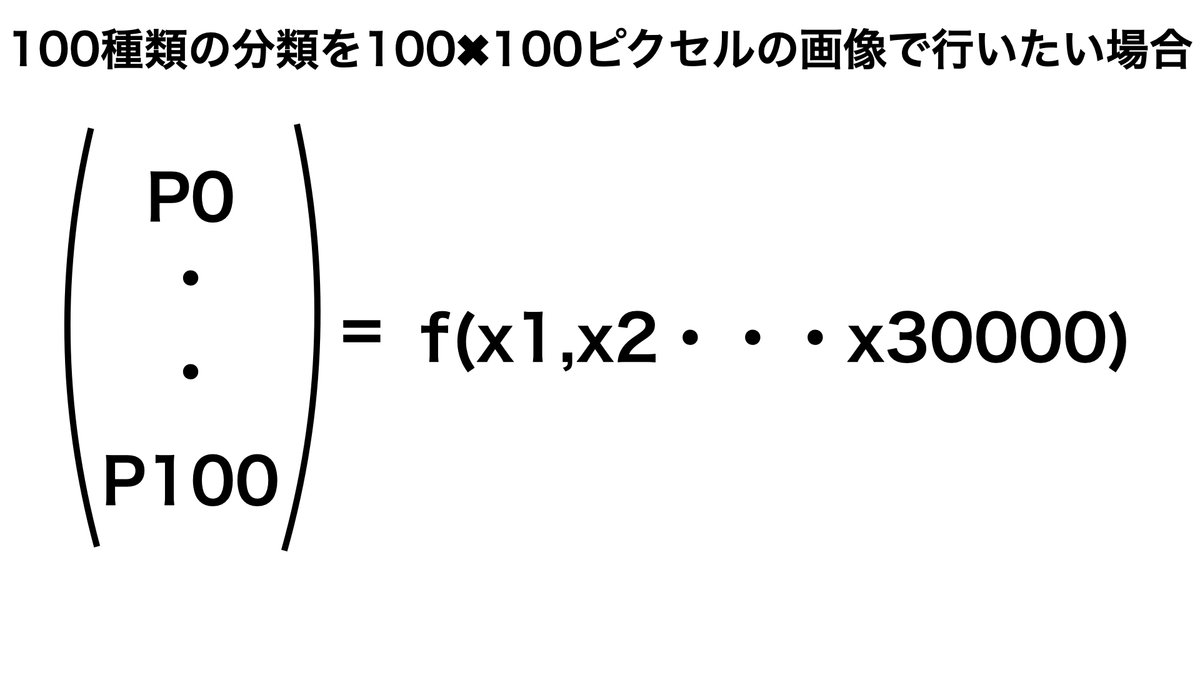
学習とは
学習とは良い関数を見つけることです。
良さを見つけるとは
良さとは誤差関数や報酬関数を設定して定量的に見つける
使う関数を決める
y=f(x)=a1+a2x2+a3x^2
でa1,a2,a3のパラメータを求めることで関数fが決まる
探す
上記のf(x)で最大にするものを探す。
つまり中学生で習ったような最大最小を求める関数を見つけることです。
すっごく単純じゃん!と思った方。確かにやってることは単純そうですね。
ただ、やってることは単純でも、その量が膨大なんです。
例えば猫の100✖︎100ピクセルの画像で256階調✖︎3を記憶させて猫と答えたいとします。
すると記憶に必要な通りは
256^3万=10^7万となります。
・・・・いくら記憶領域が大きくなっても流石に厳しいですよね。
なので、この技術を簡単に解けるようになったDeeplearningが騒がれているわけです。
どうやって簡単に解けるようになったかというと
計算を早く:GPU,TPU,MN-core
計算を楽に:mini-batch,SGD
微分を楽に:誤差逆伝播
効率的に:Adagrad,Adam,RMSprop
深さとは
それではなぜ、Deeplearningは深くしているのでしょうか?
それは、深くすることによって複雑な計算を行うことが可能になるためです。

f1(x)が二次関数の場合、二次関数にさらに二次関数をかけて4次関数にすることで複雑な波形で表すことができます。
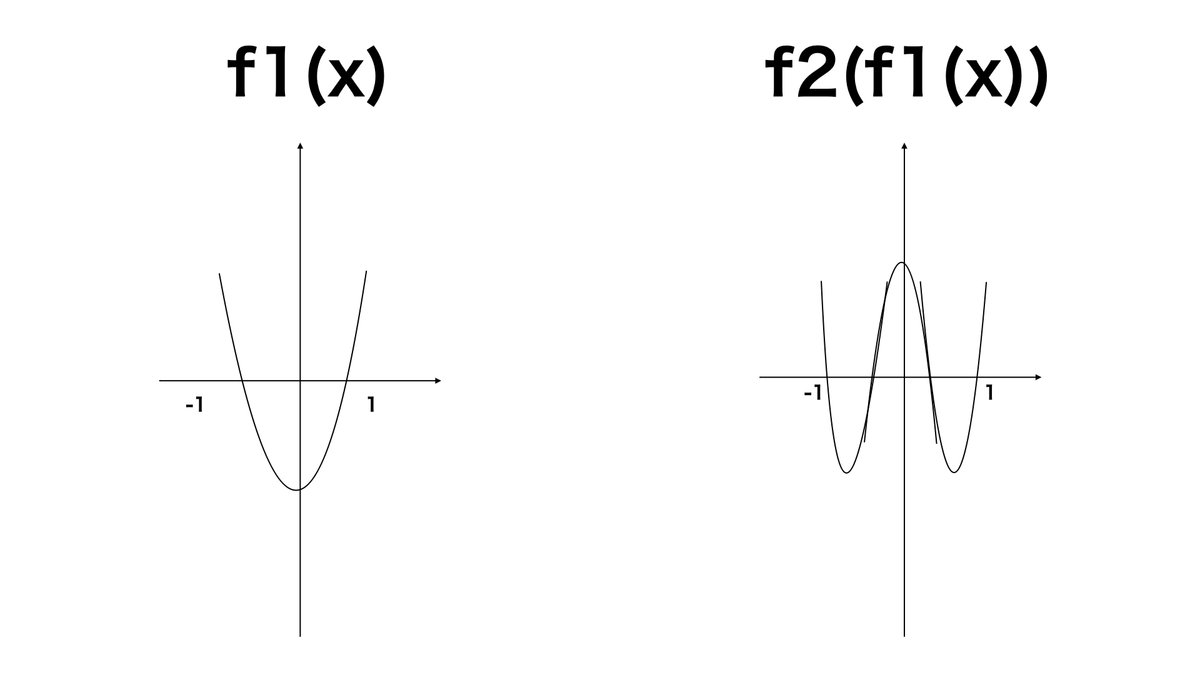
深くすることは計算の都合上も非常に合理的だと言うことです
全結合層
全ての変数を使う一番普通の一次関数のこと。
全結合層の主な目的は、前の層(例えば畳み込み層やプーリング層)から抽出された特徴を使用して、最終的な分類を行うことです。
全結合層の各ニューロンは、前の層のすべての出力に対して異なる重みを持ち、これらの重みは学習プロセス中に最適化されます。そして、各ニューロンは、これらの重み付き入力の合計に基づいて活性化関数(例えばReLUやsigmoid関数)を適用し、その結果を次の層に渡します。
入力から出力までの構造
全結合層の出力までの構造はこのようになってます。

使用するモデル

入力層から隠れ層の関数
z1 = Relu (α1✖︎x1+α2✖︎x2+・・・+α784✖︎x784)
と隠れ層に繋がる箇所を一次関数で表現できます。
隠れ層から出力における関数
y0 = Relu (a1✖︎z1+a2✖︎z2+・・・+a784✖︎z784)
y0 = Relu (a1✖︎z1+a2✖︎z2+・・・+a784✖︎z784)

最終的にこちらの関数を挟むことによって1上限で確率を出力することが可能です。
このように一次関数を用いて全てのパラメータを掛け合わせて出力することが全結合層です。
畳み込み層
主に畳み込みニューラルネットワーク(CNN: Convolutional Neural Network)という深層学習のモデルで使用される層の一つです。
畳み込み層の主な役割は、入力データ(例えば画像)から特徴を抽出することです。
これは、特定のフィルタ(またはカーネルとも呼ばれる)を使用して入力データ上をスライドさせ、そのフィルタと入力データの局所的な領域との間の畳み込み(つまり、積和演算)を計算することで行われます。
積和演算とは具体的には内積であり、畳み込みと同じ特徴を抽出することが可能。
なぜなら畳み込み層と同じ方向の内積は大きくなり、逆方向の線は小さくなるため。
こちらのアリシアさんの動画がかなりわかりやすかったのでおすすめです
具体例では丸の特徴を抽出するような畳み込みを行ってます。
畳み込み層は右上に特徴をもった正方形を表してます。
内積を取ることによって
赤色:畳み込み層と同じように右上にいくにつれて値が大きくなる箇所
緑色:左上から右下にいくにつれて大きくなる箇所

畳み込み層を使用するメリット①:局所的な特徴を抽出可能
局所的な特徴とは
境界
線
を抽出することが可能。
畳み込み層を使用するメリット①:パラメータ数が少ない
畳み込み層は画像全てにおいて共有される。
そのためパラメータ数が少なくなる。
全結合層は、縦ピクセル数✖︎横ピクセル数✖︎パラメータ数
畳み込み層は3✖︎3✖︎パラメータ数
さらにこの学習を利用することが転移学習
プーリング層
プーリング層を導入するメリットは3つです。
こちらもアリシアさんの動画をモロ参考にさせていただきました!
わかりやすすぎる。。。

プーリング層のメリット①:情報を失わず圧縮
上記の画像のように、情報量が落ちず(丸という特徴量は失わない)に圧縮(画像のピクセル量が1/4)とすることができる
プーリング層のメリット②:平行移動に対する頑健性(robustness)
背景として、コンピュータは数値が少しでもずれると、前の画像とは違ったものだと認識してしまうという特徴があります。
画像の上に犬がいるのか、画像の上からちょっとズレた箇所に犬がいるのかで全く違うものとコンピュータはとらえる。
これは人間では起きえないことですよね。

こちらのまる画像を元に説明すると今の位置で丸と読み込ませても、少しズレるとコンピュータは丸と思いません。
しかしmax poolingはある切り取った正方形の最大値を抽出する作業でした。
そのため多少のズレでも、その領域のマックス値が変わらない限りは特徴は同じものだとみなされるということです。
プーリング層のメリット③:パラメータ数削減
メリット①で表示したように、パラメータ数を削減することが可能です。
