類体論と平方剰余相互法則（その２）

　私が類体論に惹かれるのは、有理数体Ｑの有理素数ｐが、アーベル拡大体の中では「素数」ではなくなり、いくつかの素イデアルに分解すること。
そして、その分解の様子が、有理素数の「型」によって決まっている！という事実に驚くからである。

奇素数ｐの型によって、それに対応する二次形式が次のようになる。
→　p=x^2+y^2 ・・・「p≡1　 mod 4」
→　p＝x^2+2y^2 ・・・「p≡1,3 　mod 8」
→　p＝x^2+3y^2 ・・・「p≡1,3,7   mod 12」
→　p＝x^2+5y^2 ・・・「p≡1,9　 mod 20」
→　2p＝x^2+5y^2 ・・・「p≡3,7　 mod 20」
→　p＝x^2+6y^2 ・・・「p≡1,7　 mod 24」
→　　・・・　　　　　　・・・・・
どうして、このようなことが分かるのか？
素数の型と二次形式が対応するという不思議さに迫りたい。

＜平方剰余相互法則を手がかりに＞
そのために、奇素数ｐがアーベル拡大体である二次体の中で分解することと、平方剰余相互法則を手掛かりとする。

まずは、フェルマーが発見した「p≡1　 mod 4」という奇素数の型が、
二次形式「p=x^2+y^2」に対応し、「類数１」の二次体Q[i]の中で、
「p=(x+yi)(x−yi)」と分解する理由を探りたい。
具体的な例としては「p=13≡1   mod 4」が二つの素イデアルの積
「(2+3i)(2−3i)」に分解される。

＜第一補充法則を活用すると＞
それで、平方剰余相互法則の第一補充法則との関係から探ってみたい。

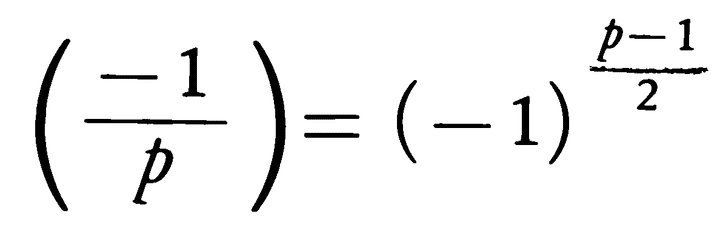
上の第一補充法則において、「平方剰余」になるためには
「指数部分」が偶数（２ｍ）でなければならない。
→(p−1)/2=2m → p=4m+1 → 「p≡1  mod 4」

＜「p≡1  mod 4」ならば「p=x^2+y^2」＞
奇素数pの型が「ｐ≡1  mod 4」ならば、「p=4m+1」と表せる。
すると、第一補充法則の（−1）の指数は(4m+1−1)/2=2m
だから(−1/p)=1となる。
つまり、「−1がｐを法として平方剰余」になるので
「x^2≡−1   mod p」に解があることになる。
その解の一つを「s」とする。
−1を移行すると、x^2+1≡0   mod p
  x=s, y=1とすると、s^2+1^2=kp     (k=1,2,3,・・・）

ここで、xとyは√pより小さいことは明らかなので
x^2+y^2は2pより小さい。
したがって、x^2+y^2=pとなるx,yが存在する。

＜「p=x^2+y^2」ならば「p≡1  mod 4」＞
ｐは奇素数なので、ｘ、ｙが同時に偶数、奇数になることはない。
それで、ｘが偶数（2m）、ｙが奇数(2n+1)とする。
すると、p=x2+y2=(2m)2+(2n+1)2=4m2+4n2+4n+1となり、
ｐは「p≡1   mod 4」型であることが分かる。

平方剰余相互法則第一補充法則からスタートして、奇素数の型とそれに対応する二次形式の姿が明らかになった。

＜2次体の姿をさぐる＞
次は、二次形式の姿から、有理数体Ｑのアーベル拡大体（ガロア拡大体でもある）になる二次体Q[i]=Q[√−1]の姿を探りたい。

二次形式の姿から、奇素数ｐはアーベル拡大体であるQ[i]の中で
「P=x^2+y^2=(x+yi)(x−yi)」と分解できる。
例えば、有理素数の「13≡1   mod 4」は、
「3^2+2^2=(3+2i)(3−2i)」と二つの積に分解される。

＜自己同型群とアーベル拡大体＞
二次体Q[i]は、有理数体Ｑの「２次」の拡大体であり、
その元は「a+bi」と表せる。

そして、Q[i]からQ[i]への自己同型群Aut(Q[i])は
｛e, f｝であり、その位数は「２」である。
e: (a+bi)→(a+bi)
f: (a+bi)→(a−bi)

拡大次数「２」と、自己同型群の位数「２」が等しいので
「アーベル拡大（ガロア拡大）」であることが分かる。
また、自己同型群は「巡回群」（f＾2=e）である。

＜判別式Dを用いた「指標」＞
ところで、二次体Q[√−1]＝Q[√d]は、
「d=−1≡3 　mod 4」だから
判別式は「D=4d=−4」となる。 

この判別式Ｄを用いた「指標」がある。
それはルジャンドル記号を一般化したヤコビ記号を用いるもので、
次のように定義される。

指標XD(p)は、「素数ｐがＤの約数なら『０』、
素数ｐが２で、２がＤの約数でなければ（2/|D| ）、
ｐが2Dの約数でない場合は（ D/p）とする。
ただし、（ */*）はヤコビ記号である。

＜「指標」の例＞
二次体Q[√−1]の判別式D=−4だから、例えば「p=13」とすると、
XD(13)＝（−4/13）となる。
ヤコビ記号の計算方法の一つに「２で割る」という操作があり、
（−4/13）＝(−1)^2（−1/13）となり、
これはルジャンドル記号と同等になるので、
平方剰余相互法則の第一補充法則により
（−1）の累乗部分は「(13−1)/2=6」なので、
XD(13)=1となる。

したがって、素数「13」は二次体Q[i]で二つの素イデアルに
完全分解することが分かる。→ 13=(3+2i)(3−2i)

このことを一般化すると次の定理になる。
XD(p)=1　⇔　pはQ[d]で完全分解　　　
（ただし、Dはdの判別式）

この定理が成り立つことを「p=17≡1 　mod 8」で確認してみる。
まず、奇素数ｐが二つの整数によって「p=x^2+2y^2」と表せることと、「p≡1,3   mod 8」が対応していることを証明する。

まず、ｘは奇数でなければならないので「x=2n+1」とする。
すると、p=(2n+1)^2+2y^2=4n^2+4n+1+2y^2
=2(2n^2+2n+y^2)+1であるから
「p≡1   mod 2」

次に、ｙが偶数の場合と奇数の場合に分ける。
ｙが偶数ならば「y=2m」とおくと、「p=4n^2+4n+1+8m^2」
なので「p≡1   mod 4」となる。

ｙが奇数なら「y=2m+1」とおくと、ｐは次のようになる。
→　p=4n^2+4n+1+8m^2+8m+2=4(n^2+n+2m^2+2m)+3
つまり、「p≡3   mod 4」

したがって、中国平方剰余公式により、「p≡1,3   mod 8」が
対応することが分かる。 

次に、「p≡1,3  mod 8」という奇素数の型が、
二次形式「p=x^2+2y^2」に対応し、
「類数１」の二次体Q[√−2 ]の中で、
「p=(x+y√−2)(x−y√−2)」と完全分解することを示す。

　例えば、「p=11≡3   mod 8」ならば
「x^2≡−2   mod 11」は解をもつ。→ x=3, 8　
→（ −2/11）＝（+1）
　あるいは、「p=17≡1   mod 8」ならば
「x^2≡−2   mod 17」は解をもつ。→x=7, 10
→（−2/17 ）＝（+1）

ｐの値が小さければ、上のように計算で求めることができるが、
ｐの値が大きくなると難しくなる。
その時は次に示す第一補充法則と第二補充法則によって
求めることができる。

例えば、（−2/11)=(−1/11)×(2/11)
=（−1)^5  ×　(−1)^15＝1

同じことではあるが、ヤコビ記号を用いる「指標」は、
「D=4d=−8」でXD(p)は次のようになる。
「p=11≡3   mod 8」⇒(−8/11)=(−1)^3×( −1/11）＝1
「p=17≡1   mod 8」⇒(−8/17)=(−1)^3×( −1/17）＝1
　したがって、「p=11, 17」のどちらも二次体Q[√−2]の中で
二つの素イデアルに分解することになる。

＜三個が対応する＞
　すなわち、次のように三個の概念が対応している。
「p=x^2+y^2」・・  「p≡1   mod 4」・・・ XD(p)=1
「p=x^2+2y^2」・・「p≡1,3   mod 8」・・  XD(p)=1
「p=x^2+3y^2」・・「p≡1,3,7 mod 12」・・XD(p)=1
「p=x^2+5y^2」・・「p≡1,3 ,7,9 mod 20」・XD(p)=1
「p=x^2+6y^2」・・「p≡1,7 mod 24」・・   XD(p)=1
        ・・・　　　　　・・・　　　　　　　　　・・・

＜ミンコフスキーの指標：M＞
ドイツの数学者、ヘルマン・ミンコフスキーは「格子点」を用いた整数論を展開した。そのミンコフスキーにちなむ指標にＭがある。

それは、判別式が「D＞0」ならM=√D/2であり、
「D＜0」ならM=√ /3である。

このＭを用いて次の集合を定める。
→　集合Ｓ＝｛p|　p≦MかつXD(p)≠1｝

二次体Q[√−2]について、集合Ｓを求めてみる。
まず、D=−2×4=−8である。
そして、M=√2.666・・≒1.63であるから、
集合Ｓは空集合になる。
つまり、Q[√−2]の中には「単項イデアル以外は存在しない」
ことを意味する。

同じように、二次体Q[√−5]について、集合Ｓを求めてみる。
まず、D=−5×4=−20である。
そして、M=√6.66・・≒2.58
それで、集合Ｓは２以下の素数の集合なので｛2｝となる。
もちろん、XD(2)＝（−20/2）＝0≠1である。

それで、「２」を割る（分割する）素イデアルを探すと、
「単項イデアルではない」次のような素イデアルが見つかる。
→　(2, 1+√−5)(2, 1−√−5)＝2

このことから、二次体Q[√−5]の素イデアルは、
単項イデアルの集合Ａと、
(2, 1+√−5)の倍数である単項イデアルでない素イデアルの集合Ｂの
二種類であることが分かる。
つまり、二次体Q[√−5]の類数は「２」であることが分かる。

そして、この二つの集合｛Ａ、Ｂ｝は次のように
乗法群（イデアル類群）になる。

 集合Ｂの二つの素イデアルの積を（例として）計算してみると
次のように集合Ａの元になる。→B×B＝A
(2, 1+√−5)(3, 1+√−5)　　　　・・・・２項×２項
＝(6, 3(1+√−5), 2(1＋√−5), (1+√−5)^2) 　・・・４項
＝((1+√−5)(1−√−5), 3(1+√−5), 2(1＋√−5), (1+√−5)^2)
＝(1+√−5)(1−√−5,   3,   2,   1+√−5)・・・共通因数
＝(1+√−5)(1)＝(1+√−5)・・・・・・最大公約数は(1)

＜素イデアルの証明＞
また、p＝(3+2√−5)とすると、そのノルムは次のようになる。
→　N(p)＝(3+2√−5) (3−2√−5)＝9+20=29
ノルムが有理素数になるので、ｐは素イデアルであることが分かる。 

同様に、単項イデアルでない場合も、そのノルムが有理素数であれば
「素イデアル」であることが分かる。
例えば、p＝(3, 1+2√−5)とすると、
N(p)＝(3, 1+2√−5)(3, 1−2√−5)・・・共役なイデアルの積
＝（9,  3(1+2√−5),  3(1−2√−5),   21）
＝(3)×(3,   (1+2√−5),   (1−2√−5),      7)・・・共通因数
＝(3)×(3,   (1+2√−5),   2−(1+2√−5),   7)
＝(3)×(3,   (1+2√−5),    2,    7)　・・ 最大公約数は(1)
＝(3)×(1)=(3)＝3
「３」は有理素数なので、ｐは素イデアルであることが分かる。

＜対応する2次体＞
さて、二次体Q[√−5]の素元の例として、
Ａに属する単項の素イデアルである(3+2√−5)と、
Ｂに属する単項でない素イデアル（3, 1+2√−5）を示した。
この二つの素イデアルに対応する二次体は次のようになる。

前述のように、(3+2√−5)のノルムは「29」であるから・・
P=29≡9 　mod 20 ・・「x^2+5y^2=29」の解→（x=3, y=2）

また、前述のように、Q=(3, 1+2√−5)は、
(2, 1+√−5)との積で単項イデアル(1+√−5)になり、
ノルムは「３」である。
P=3≡3   mod 20 ・・「x^2+5y^2=2×3」の解→ (x=1, y=1)

つまり、二次体の解で求められる(1+√−5)は、
そのノルムが合成数「６」であり、素イデアルではない。
それで、単項イデアルでないＢの元だとすれば、
(2, 1+√−5)×Q＝( 1+√−5)となるはずである。

整理すると、p=3≡3 　mod 20に対応する二次形式は・・・
→　x^2+5y^2=2p　となる。

＜その「逆」を示す＞
「2p」は偶数であるから
【ｘが奇数(10n+1)でｙも奇数(2m+1)の場合】
⇒  x^2+5y^2
=100n^2+20n+1+5×(4m^2+4m+1)
＝20(5n^2+n+m^2+m)+6
つまり、「2p≡6   mod 20」→「p≡3   mod 20」

同様に・・・
【ｘが奇数(10n+3)でｙも奇数(2m+1)の場合】
⇒  x^2+5y^2
=100n^2+60n+9+5×(4m^2+4m+1)
＝20(5n^2+3n+m^2+m)+14
つまり、「2p≡14   mod 20」→「p≡7   mod 20」

初等的な方法ではあるが、「x^2+5y^2=p」について次のように証明することができる。
【ｘが奇数(10n+1)でｙは偶数(2m)の場合】
→　x^2+5y^2
=100n^2+20n+1+5×(4m^2)
＝20(5n^2+n+m^2+m)+1
つまり、「p≡1   mod 20」

【ｘが偶数(10n+2)でｙが奇数(2m+1)の場合】
→　x^2+5y^2
=100n^2+40n+4+5×(4m^2+4m+1)
＝20(5n^2+2n+m^2+m)+9
つまり、「p≡9   mod 20」

＜平方剰余相互法則を用いると＞
平方剰余相互法則を活用することによって、これまでの初等的な記述が、
次のように統一的で鮮やかに示すことができる。

「XD(p)=1」であることを仮定する。
（もちろん、D=4d=4×(−5)=−20である。）
XD(p)＝（−20/p）＝(−4/p)×（5/p）＝1
ただし、（ −4/p）＝（ −1/p）であり、（ 5/p）＝（p/5 ）である。

したがって、(−4/p)＝1かつ（5/p ）＝1 の場合は次の通り
「P≡1  mod 4」かつ「p≡1,4  mod 5」
つまり、「p≡1,9   mod 20」
そして、この型の奇素数ｐは「p=x^2+5y^2」となり、
そのｐの集合は単項イデアルの集合（Ａ）になる。

また、( −4/p)＝−1かつ（ 5/p）=−1 の場合は次の通り
「p≡3   mod 4」かつ「p≡2,3   mod 5」
つまり、「p≡3,7   mod 20」
そして、この型の奇素数ｐは「2p=x^2+5y^2」となり、
そのｐの集合は単項イデアルでない集合（Ｂ）となる。

＜まとめ＞
証明の有無や正確性について異論があるのは承知の上であるが、
類体論と平方剰余相互法則が深く結びついていることは
明らかになったと思われる。