
偶数と奇数(2)
<ゴールドバッハ予想>
旧プロイセン王国(首都はベルリン)に生まれたクリスチャン・ゴールドバッハ(1690~1764)は、数学者オイラーに宛てた書簡の中で次のように述べている。
「四以上の全ての偶数は二つの素数の和で表せる」
これが、ゴールドバッハ予想と呼ばれるもので、2023年現在も証明されていない。
(例) 4=2+2 6=3+3 8=3+5
その後、ゴールドバッハは次のような「弱いゴールドバッハ予想」を発表する。
「7以上の全ての奇数は三個の素数の和で表せる」
(例) 7=2+2+3 9=3+3+3 11=3+3+5
この「弱いゴールドバッハ予想」は、2013年にハラルド・ヘルフゴットによって証明されたという。
<偶数の分解から合成へ>
さて、ゴールドバッハ予想は、「弱いゴールドバッハ予想」も含めて、偶数や奇数を二つ、あるいは三つの素数に「分解」できることを示そうとする。
これを、二つ、あるいは三つの素数和として、偶数や奇数を「合成」する方向で考えてみたい。
すなわち、4以上の全ての偶数を二つの素数の和として実際に「合成」してみるのである。
その場合のルールとして、例えば「3+13」と「5+11」のように二種以上の合成方法がある時は、「小さい方の素数」が最小になる合成方法(「3+13」)を採用することにする。
(試行してみると次の表のようになる。「4から84まで」の偶数を合成したものである。また、合成された奇数はオレンジで示したように「双子素数」になる。)

<奇数の分解から合成へ>
次に、「弱いゴールドバッハ予想」について考える。全ての奇数を三個の素数の和として「合成」してみるのである。
「2」以外の素数は奇数であるので、三個の素数和は奇数になることは明らかである。
そして、「ゴールドバッハ予想」が正しければ、全ての偶数は二個の素数和で表されるので、次のようになる。
→ (素数A+素数B)+素数C=偶数D+素数C
偶数Dを最小にする組み合わせで、全ての奇数を合成する試みの一端を次に示す。(「5から67まで」の奇数の合成)

<偶数と奇数の関係>
改めて、偶数と奇数の関係は面白く深いことが分かる。
剰余類として、「2で割った余り」によって、自然数を偶数と奇数に分ける場合には、偶数と奇数は対等に見える。
しかし、自然数が並ぶ中から偶数だけを持ち上げた次の図(下)を参照すると、決して対等には見えない。
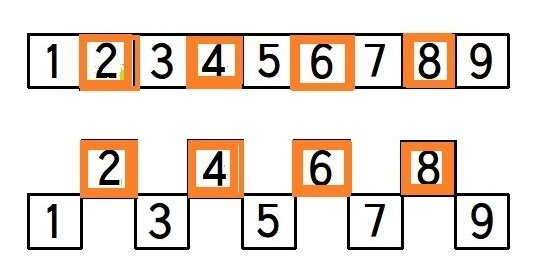
「2」以外の素数は奇数の中にある。
そして、奇数の中の素数が偶数を支えているように見える。
もちろん、自然数全体は素数の積や和によって表すことができる、という
意味で、素数に支えられている。
そして、偶数はさらに強く素数によって支えられている。そのことを教え
てくれるのが、ゴールバッハ予想なのかも知れない。
<奇数と素数の関係>
ところで、ガウスは自然数の中の素数の出現率から「ガウスの素数定理」
を発見した。また、オイラーは自然数全体を用いて「素数階段」を描いた。
しかし、「2」以外の素数は奇数の中にある。したがって、奇数の中で素数の出現率の変化を探り、奇数全体を用いて「素数階段」を描くこともできるはずである。
(次図が奇数だけの素数階段である。素数になると一段あがる。)

<偶数の「次数」>
なお、偶数aを素数の積に分解した時、「2」の個数を偶数aの「次数」と呼ぶことにする。
例えば、偶数「8」や「24」は「3次の偶数」である。「3次の偶数」は「3回2で割る」と奇数になる。
つまり、当然のことではあるが、全ての偶数は「数回2で割る」と奇数になる。
(次図は因数「2」の個数により持ち上る程度を変えてある。)

<奇数を偶数に変える>
奇数は「3倍して1をたす」と偶数になる。例えば、奇数「5」は「3倍して1をたす」と偶数「16」になる。偶数「16」は「4次の偶数」だから「4回2で割る」と奇数「1」になる。
奇数は「1をたす」だけで偶数になる。それを、コラッツはあえて「3倍して1をたす」ことにした。すると、必ず「1」に辿り着くだろう、というのが「コラッツ予想」である。
<ゴールドバッハ予想とコラッツ予想>
ゴールドバッハ予想は、偶数を二個の(2以外の)奇数である「素数の和」で表すことが「できるだろう」と予測する。
二個の素数それぞれを「3倍して1をたす」とその和は偶数になる。「2で割る」とどうなるのだろう。
もしかすると、「ゴールドバッハ予想」は「コラッツ予想」と繋がっているのかも知れない。
