本選出場者が語る！ 数学オリンピックの知られざる世界

皆さんこんにちは！
ドラゴン桜塾塾長の永田耕作です。 

みなさんはテレビやネット等で「日本の高校生が数学オリンピックでメダル獲得！」というニュースを目にしたことはありませんか？
 
学問のオリンピックは化学や物理など色々なジャンルで開催されているのですが、今回はその中でも数学のオリンピックについて紹介しようと思います。

以前このnoteでも少しだけお話ししましたが、僕は日本数学オリンピックへの出場経験があります。
 
高校2年生で出場し、予選を突破して本選（全国大会）までたどり着くことができました。
 
「数学オリンピック」と聞くと、どうしても難しいというイメージを持つ人が多いと思います。
 
もちろんそのイメージ通り、全ての問題を解くのは大変困難です。
 
しかし、中には中学校、高校で習った知識だけで解ける問題も入っているのです。
 
今回は実際に出場経験のある僕が、出場した年の問題も紹介しながら数学オリンピックの中身や舞台裏について解説していきます！

①そもそも「数学オリンピック」とは

本題に入る前に、数学オリンピック（略して数オリ）の歴史について簡単におさらいしましょう。
 
先日までフランスのパリでオリンピックが行われていましたが、数オリも同じように「世界大会」です。

普通のオリンピックと違うのは、4年に1回ではなく毎年開催される点ですね。

その国内予選に、塾長である僕は出場したのです。
 
国際数学オリンピック（世界大会）が初めて開催されたのは今からなんと65年前の1959年で、場所はルーマニアでした。
 
日本が初めて参加したのは1990年（平成2年）で、そこから毎年「日本数学オリンピック（JMO）」によって「国際数学オリンピック（IMO）」に参加する選手を決定しているのです。

ちなみに、2003年には東京で、そして2023年には千葉で国際大会が開かれています。

そんな数学オリンピックですが、毎年どのくらいの人が予選に、そして本選に出場していると思いますか？

もちろん年度にもよるのですが、例えば僕が出場した2019年の予選では、4423人の選手がエントリーしていました。
 
それに対して、この予選を突破して本選に進んだ人はたったの303人。
 
つまり、9割以上の人が予選で落とされていることになります。

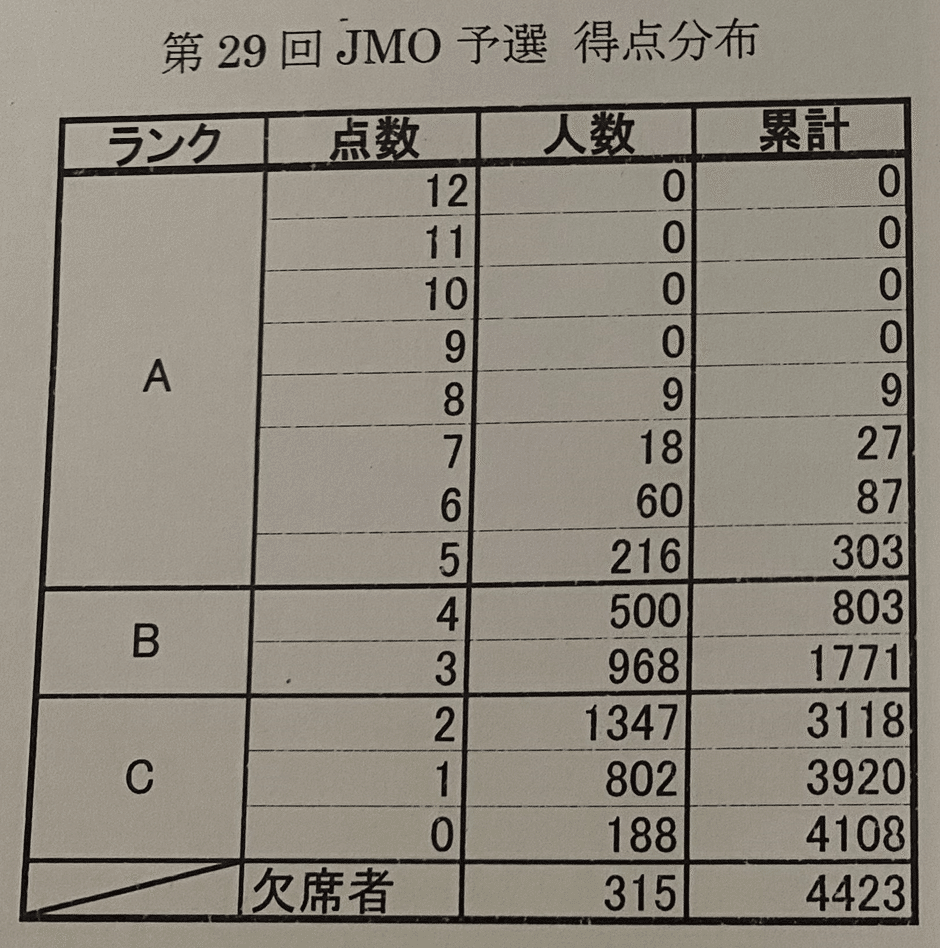
この表を見て下さい。これは、予選を突破した僕に実際に送られてきたハガキの写真です。
 
この試験での僕の点数は6点で、成績はAランクとなっています。
 
5点以上がAランクとされていて、このランクを獲得できると、本選に出場できることになります。

この表を見ていただければ分かると思うのですが、予選に参加した4423人の最高点が「8点」です。
 
つまり、12問中4問は全国の数学マニアが誰も解けなかった問題ということです。
 
ここまであえて説明していなかったのですが、数学オリンピックの予選の問題は「記述式」ではありません。

12問、全て答えだけを記入する問題です。
 
つまり、適当に書いたって当たる可能性さえあるのです。
 
それでも、全国の名だたる有名校から集まった数学の猛者が誰も解けなかった問題と考えると、とても恐ろしいレベルなのがわかっていただけるのではないでしょうか。

ただ、冒頭にも書いたように、すべての問題が難しいわけではありません。
 
第1問から第12問まで、難易度が順に加速度的に上がっていく試験になっていて、第3問くらいまでは中学生くらいまでで学習する知識で十分戦える問題になっているのです。

ここからは、実際の予選問題を見て、数学オリンピックの独特な世界観を体験してみましょう！ 

 

②2019年数学オリンピック予選の問題に挑戦！

今回みなさんにご紹介するのは、僕が参加した2019年数学オリンピック予選の第2問です。
 
問題はこちらです！

２．どの桁（けた）も素数であるような正の整数を良い数という。３桁の良い数であって、２乗すると５桁の良い数になるものをすべて求めよ。 

おそらく多くの人がこの問題を見て、「良い数ってなんだ…？」と感じたことでしょう。

実はこれこそが、数学オリンピックの真髄です。
 
この試験では毎年新しい公式や、「良い数」のような新しい概念が登場するのです。

しかし、怖気付く必要はありません。
 
新しい考え方が出てくる際にはルールが必ず示されているので、それに従って計算をするだけです。
 
既存の考えにとらわれずにその場で対応する、柔軟な姿勢が重要になるのですね。
 
さてこの問題、どのように解き進めれば良いのかというと、ポイントはズバリ「素数のかけ算」です。
 
1桁の数字の中で素数であるものは「2,3,5,7」の4種類であるため、問題の条件を満たす「良い数」は全て2,3,5,7のどれかで構成されていることが分かります。

しかしこれだけでは、まだまだ候補を絞り込むことはできていません。
 
ここで重要になるのは、「1の位だけを2乗してみる」というプロセスです。

どんな数字であれ、2乗したときの1の位は、もともとの数の1の位を2乗することで求めることができます。
 
例えば「2」を2乗すると「4」になりますが、1の位を「2」で固定した、他の数字の2乗の結果を見てみましょう。
 

12×12＝144
392×392＝153664
1852×1852＝3429904 

こんなふうに、どれだけ元の数が大きくなっても、2乗した数の1の位は「4」で同じですね。

これを利用すると、求める数の1の位が「5」であることが分かります。
 
他の数字だと、2乗した際に素数でない数字が出てきてしまうからです。
 
気になる人は、ぜひ自分で計算して確かめてみてください。

これで1の位は分かったので、次は「2乗すると5桁になる」という部分に着目しましょう。
 
3桁の数字を2乗した場合、元の数の大きさによって2乗の結果が5桁になる場合と、6桁になる場合が存在します。
 
2乗して100000になる数は

√100000 = 316.227766…

であるため、求める数字は316より小さいことが分かります。
 
さらに言えば、仮に5桁の数字になったとしても「9万いくつ」というような数字であれば、「9」がすでに素数ではないため条件に当てはまらないことが分かります。
 
よって、百の位が「2」であることが分かるのです。
 
ここまで絞り込むことができれば、あとは「225,235,255,275」の4種類を確かめるだけですね。
 
この問題の最終的な答えは動画で解説しているため、ぜひ下にあるリンクからチェックしてみてください！ 

 

おわりに

今回は「数学オリンピックの知られざる世界」ということで、数オリの歴史や問題などを紹介してきました。

最終的な問題の答えやより詳しい解説は、僕が塾長を務めるYouTubeチャンネル「ドラゴン桜塾」で紹介しています。
 
最後の問題の解説だけでなく、ここでは書かなかった「本戦出場者が日本代表に選ばれるまでどうふるい分けられるか」についても話しているので、ぜひご覧ください！ 

今回の記事は、ここまでとなります。
それではまた次回の記事でお会いしましょう！