
意外と知られていない化学の法則
化学基礎を習った文系理系の皆さん、まず次の問題を解いてみてください。
濃度98.0%、密度1.80g/cm^3の濃硫酸100mlを水で希釈して、濃度18.0%、密度1.40g/cm^3の希硫酸を調製したい。必要な水と、得られる希硫酸の体積はそれぞれ何cm^3か。
ただし、H₂SO₄の分子量は98.0、水の密度を1.00g/cm^3とする。
では最初に2種類の誤答例と、2種類の正答例を書きます。ある程度
目を通してください。
また、解答例に限らず、何か引っかかるなというところがあったら、
深く考えすぎず一旦飛ばしてみてください。
説明の都合上H₂SO₄aqを硫酸水溶液、H₂SO₄を硫酸水溶液に含まれている硫酸、
希釈前のH₂SO₄aqを①、希釈後を②とする。
単位は[]の中に表記し区別する。
誤答例(i)
②のH₂SO₄aqをV₁[cm^3]とする。
「①のときのH₂SO₄の物質量は
$$
(H₂SO₄の質量[g])*\frac{[mol]}{98[g]}
$$
で表せる。
また、①のH₂SO₄aqの質量は
$$
100[cm^3]*\frac{1.80[g]}{[cm^3]}
$$
$$
=100*1.80[g]
$$
そのうち、98%がH₂SO₄の質量なので、H₂SO₄の質量は
$$
100*1.80[g]*0.98
$$
したがって、H₂SO₄の物質量は
$$
100*1.80[g]*\frac{98}{100}*\frac{[mol]}{98[g]}
$$
$$
=1.80[mol]
$$
」…(*)
また、②の状態のときのH₂SO₄の物質量は(*)と同様にして、
$$
V₁[cm^3]*\frac{1.40[g]}{[cm^3]}*\frac{18}{100}*\frac{[mol]}{98[g]}
$$
$$
=V₁*1*\frac{18}{10^3}*\frac{[mol]}{7}
$$
反応の前後でH₂SO₄の物質量は変わらないので、
$$
V₁*\frac{18}{10^3}*\frac{[mol]}{7}=1.80[mol]
$$
$$
v=700
$$
加えた水の体積は
$$
700[cm^3]-100[cm^3]=600[cm^3]
$$
求める値は
加えた水の体積600[cm^3],得られるH₂SO₄aqの体積700[cm^3]
誤答例(ii)
加えた水の体積をV₂[cm^3]とする。
①の状態のH₂SO₄の質量は(i)の(*)の過程を利用して
$$
100*1.80[g]*0.98
$$
②の状態のH₂SO₄の質量は、H₂SO₄aqの体積は(100+V₂)[cm^3]であるから
同様にして
$$
(100+V₂)[cm^3]*\frac{1.40[g]}{[cm^3]}*0.18
$$
$$
=(100+V₂)*1.40[g]*\frac{18}{100}
$$
反応の前後でH₂SO₄の質量は変わらないので、
$$
(100+V₂)*1.40[g]*\frac{18}{100}=100*1.8[g]*\frac{98}{100}
$$
$$
V₂=600
$$
よって得られるH₂SO₄aqの体積は
$$
(100+600)[cm^3]=700
$$
求める値は
加えた水の体積600[cm^3],得られるH₂SO₄aqの体積700[cm^3]
正答例(iii)
②のH₂SO₄aqの体積をV₁[cm^3]とする。
①のH₂SO₄の質量は(ii)と同様にして
$$
100*1.80[g]*\frac{98}{100}
$$
②のH₂SO₄の質量も同様にして
$$
V₁[cm^3]*\frac{1.40[g]}{[cm^3]}*\frac{18}{100}
$$
反応の前後でH₂SO₄の質量は変わらないので、
$$
V₁[cm^3]*\frac{1.40[g]}{[cm^3]}*\frac{18}{100}=100*1.80[g]*\frac{98}{100}
$$
$$
V₁=700
$$
①の状態のH₂SO₄aqの質量は
$$
100[cm^3]*\frac{1.80[g]}{[cm^3]}
$$
加えた水の質量は、
$$
700[cm^3]*\frac{1.40[g]}{[cm^3]}-100*1.80[g]
$$
$$
=800[g]
$$
水の密度は1.00[g/cm^3]であるから
$$
800[g]*\frac{[cm^3]}{1.00[g]}
$$
求める値は
加えた水の体積800[cm^3],得られるH₂SO₄aqの体積700[cm^3]
正答例(iv)
加えた水の体積をV₂[cm^3]とする。
①のH₂SO₄の質量は
(①のH₂SO₄aqの質量[g])*(①の濃度)である。
よって
$$
(100[cm^3]*\frac{1.80[g]}{[cm^3]})*\frac{98}{100}*\frac{[mol]}{98[g]}
$$
$$
=1.80[mol]
$$
②のH₂SO₄aqの質量は、(①のH₂SO₄aqの質量[g])+(加えた水の質量[g])である。
①のH₂SO₄aqの質量は
$$
100[cm^3]*\frac{1.80}{[cm^3]}
$$
$$
=180[g]
$$
加えた水の質量は水の密度1.00[g/cm^3]を用いて
$$
V₂[cm^3]*\frac{1.00[g]}{[cm^3]}
$$
$$
=V₂[g]
$$
②の物質量は
(②のH₂SO₄aqの質量[g])*(②の濃度)*(物質量の逆数[mol/g])であるから、
$$
(180[g]+v[g])*\frac{18}{100}*\frac{[mol]}{98[g]}
$$
$$
=\frac{(180+v)*18}{100*98}[mol]
$$
反応の前後でH₂SO₄の物質量は変わらないので
$$
=\frac{(180+V₂)*18}{100*98}[mol]=1.80[mol]
$$
$$
V₂=800
$$
②のH₂SO₄aqの体積は
(②の水溶液の質量[g])*(②の密度の逆数[cm^3/g])であるから
$$
(800+180)[g]*\frac{[cm^3]}{1.40[g]}
$$
$$
=700
$$
求める値は
加えた水の体積800[cm^3],得られるH₂SO₄aqの体積700[cm^3]
誤答例では何を間違えたのか、正答例はどうして矛盾が生じていないのかが
何となく分かりましたか?
では、何が違っていて、どうして間違いなのかをこれから話します。
ですが、せっかく問題に目を通してもらったみなさんには、化学を好きになってほしい、できる理系の考え方を知ってほしいので(i)~(iv)のあらゆる点について触れながら解説していきます。
1.分数の掛け算
解答例は全てとにかく単位を掛け算で変形しまくると言う方法をとりました。
個人的にはやくておすすめな方法です。
これに関しては過去に記事を作ったので、
すぐ下にあるバナーをタップして見てください。
2.物質量と質量は同値である
化学基礎でmolについて習っていない人、またはmolについてよくわかっていない人向けに解説します。
そもそもmolは、原子や分子を6.0*10^23個集めた塊のことを指します。
式で表すと$${1[mol]=6.0*10^{23}[個]}$$です。
原子分子は1個1個がとても小さいです。水分子1つだけ摂取しても感覚的には何も変わらないですよね?
このように、原子分子を1個ずつ見ても現実的に大して変わらないから、いっぱい集めた6.0*10^23[個]で考えるのです。
そのとき、いちいち6.0*10^23[個]と記述するのがめんどくさいから新たに[mol]
という単位を定めたのです。
では、なぜ10^23[個]や、10^25[個]ではなく、
6.0*10^23[個]を1[mol]と定義したのでしょうか。
それは、6.0*10^23[個]の原子で、陽子と中性子を足した値である質量数に
一致することがわかったからです。
質量数が12の原子(C)は6.0*10^23[個]集まると12[g]に、
質量数が1の原子(H)は6.0*10^23[個]集まると1[g]になります。
以上より、$${=6.0*10^{23}[個]=1[mol]}$$
因みに質量数の単位がない理由は、基本的な炭素原子1個の陽子と中性子の数の和である12を基準として、相対的に他の原子がどのような質量になるかを考えたものであるからです。
取り敢えず[mol]があまりよくわからない人は、大量に集めた原子の数か、
原子の質量をひと塊としてみているくらいに思ってください。
3.H₂SO₄の質量の求め方について
密度、質量パーセント濃度、分子量の3つがあれば、H₂SO₄aqの体積から物質量[mol]の情報に持っていけます。
ここからは1.の計算方法はわかっているものとして話をします。
また、先に図を表示しておきます。
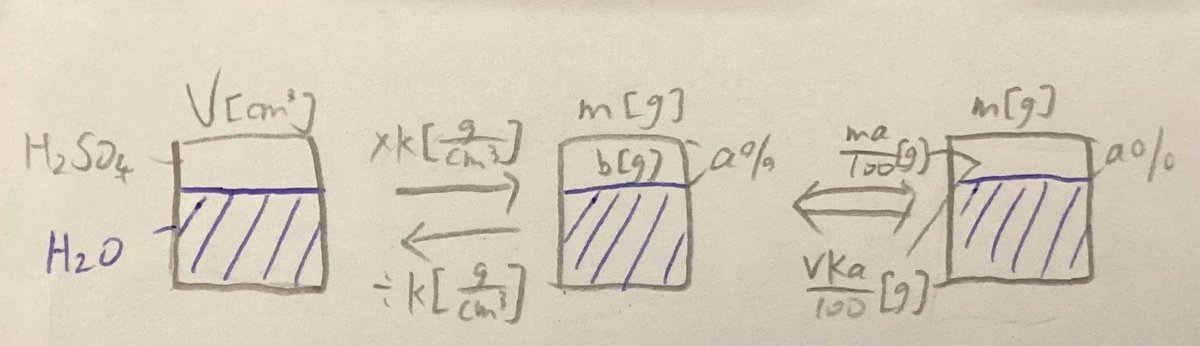
H₂SO₄aqの体積を新たにV[cm^3],そのときの物質量をm[g]とします。
体積から物質量に変換するので
$$
V[cm^3]*\frac{k[g]}{[cm^3]}=m[g]
$$
kは定数とする。
(気体定数みたいに、)kは等式を成り立たせるためだけに単位をつけました。しかし、[g]と[cm^3]を直接変換する単位である密度が今回は幸いにもありますね。
なので、kは密度の値であり、上の式は
$$
m[g]=V*\frac{k[g]}{1}
$$
となります。
m[g]はH₂SO₄aq全体の質量を表しています。
ここまでが、図の左側の2個の四角が表す内容です。
では、m[g]をどのようにしたらH₂SO₄aqに含まれるH₂SO₄になるのでしょうか。
ここで、質量パーセント濃度の定義を確認します。
質量パーセント濃度は
"溶液100gあたりの溶質の質量を表すもの。"です。
これを式にして表すと、
$$
\frac{溶質の質量[g]}{溶液の質量[g]}*100
$$
質量パーセント濃度の単位は無次元になっているけれど、
元々は[g]を[g]で割ったものとなります。
また、計算式と濃度の表記を行き来するときに100を掛けたり割ったりするのは、しっかり定義を押さえておけば妥当な考え方になります。
計算の時には単位を毎回使います。しかし、使う単位の定義を勘違いしていると計算にずれが生じます。なので、定義もしっかり抑えておくようにしましょう。
もう一度言います。定義は正しく頭に入れておきましょう。
話を戻して、溶液の質量を表すm[g]を、
どのようにしたらH₂SO₄aqに含まれるH₂SO₄になるのでしょうか。
H₂SO₄aqの質量パーセント濃度をa[g/g]
欲しい情報である、H₂SO₄の質量をb[g]、とします。
先ほど確認した定義通りに式を立てると、
$$
\frac{b[g]}{m[g]}*100=a[g/g]
$$
$$
b[g]=\frac{ma}{100}[g]
$$
[g]一つだけ約分してみました。すると、このような関係式が得られます。
m[g]をさきほど求めた式を用いてVk[g]と表記しても良いです。
これで、図の全貌がわかったのではないでしょうか。
因みに(iv)の序盤にある
「①のH₂SO₄の質量は
(①のH₂SO₄aqの質量[g])*(①の濃度)である。」
という文章が正しいことはもう分かるはずです。
一個上の式の文字の定義を再確認すると、
b[g]は溶質の質量
m[g]は溶液の質量
a[g/g]は溶液の質量パーセント濃度
「」内において、溶質が①のH₂SO₄の質量、溶液が①のH₂SO₄aqの質量[g]、
濃度はそのまま照らし合わせたら全く同じになりますね。
本題:誤答例は何を間違えているのか
では、本題である誤答例の間違いを説明します。
結論から言うと、
希釈の前後で体積は保存しない、数式で表すと、
$${(①のH₂SO₄aqの体積[cm^3])+(加えた水の体積V₂[cm^3])≠(②のH₂SO₄aqの体積V₁[cm^3])}$$
となるためです。
「じゃあ何が正しいの?」
正しいのは
$${(①のH₂SO₄aqの質量[g])+(加えた水の質量V₂[g])=(②のH₂SO₄aqの質量[g])}$$
です。
何でやねん!と思った方はラボアジエが提唱した質量保存の法則が鍵となります。
質量保存の法則の定義についてここで改めて確認します。
化学変化がおこる場合、化学反応の前後で物質全体の質量は変わらない法則
まあそれが正しいことは実験によって得られたものであるから置いておいて、逆に何故体積は保存できないと言い切れるのでしょう。
それは、高校化学の教科書に載っている保存する量は
質量[g],物質量[mol]
エネルギー[J]
電荷[C]
しかありません。長年議論や実験を重ねた挙句高校化学までの学習においては、これら以外は原則保存しないことが分かっています。
体積に関しては、希釈をはじめとする、体積を増やす反応において単純な和にならず、和より小さくなる収縮という現象が起こることが確認されています。
保存する法則は知られていても、保存しないという法則にみなさんは気づいていたでしょうか。(正直なところ、保存しない法則などただの事実に過ぎないので、法則と呼ぶ方がおかしい気もしますが、その点にはあまり気にしないでください。)
因みに、質量と物質量をまとめたのは、過去の記事でも触れた通り、
$${(原子量)[g]=(物質量)[mol]}$$
となるためです。
等号で結ばれているものは同じものを表すのが等式の前提事項です。
また、質量と物質量には多少のニュアンスの違いしかなく、それは
質量そのものに着目しているか、ある程度まとまった個数を軸として着目しているかの違いでしかありません。
因みにこの問題…
因みにこの問題は自作したのですが、有り得ない問題でもあります。
何があり得ないかというと、密度1.40[g/cm^3]、濃度18%のH₂SO₄aqは
存在しないということです。
密度1.40[g/cm^3]の硫酸の濃度は50%
濃度密度表というものを見ると、明らかにあり得ない濃度になっているのです。
約分しまくれば掛け算をする回数が少なくかつ綺麗な値になるように問題を作ろうとしたらこうなりました。
理科という学問は、自然現象を最優先に考えてどのような論理がありそうかを追求する学問であるゆえ、入試化学において、現実的にあり得ない値または状態の問題が出てくることはありません。
これを利用して、例えば何らかの物質の原子量を求める問題で、答えが1未満になった、液体の密度を求める問題なのに、重金属の密度(10[g/cm^3]くらい)になったというのは計算または立式を間違えたことが分かります。
教科書に載っている物質に関する情報は覚えておくと、求めた解が正しそうかを考えるための指標になるので、真っ先にとは言いませんが、
ある程度まとめて覚えておくと得だと思います。
アウトプットをしよう!
長々と僕の主張だけを読んでいても仕方がないので今度は現実的にあり得る値の問題を解いてみてください。さっき解けなかった人はここで解けるようにしっかり考えつつ、前の話に戻ったりしながら頑張って解いてください!
濃度95.0%、密度1.84 g/cm³の濃硫酸200 cm^3を水で希釈して、濃度20.0%、密度1.12 g/cm³の希硫酸を調製したい。必要な水と、得られる希硫酸の体積はそれぞれ何cm³か。ただし、H₂SO₄の分子量は98.0、水の密度を1.00 g/cm³とする。
個人的に一番簡単そうな解法を以下に示します。
加える水の体積をV[cm^3]とする。
希釈前のH₂SO₄の質量は
$$
200[cm^3]*\frac{1.84[g]}{[cm^3]}*\frac{95.0}{100}
$$
$$
=1.84*95.0*2[g]
$$
希釈後のH₂SO₄の質量は
$$
(200[cm^3]*\frac{1.84[g]}{[cm^3]}+V[cm^3]*\frac{1.00[g]}{[cm^3]})*\frac{20}{100}
$$
$$
=(200*1.84+V)[g]*\frac{1}{5}
$$
と表せる。
反応の前後でH₂SO₄の質量は変わらないので、
$$
(200*1.84+V)[g]*\frac{1}{5}=1.84*95.0*2[g]
$$
$$
1.84*200+V=1.84*950
$$
$$
V=1.84*(950-200)
$$
$$
V=1380≒1.38*10^3
$$
希釈前のH₂SO₄aqの質量が
$$
\frac{1.84[g]}{[cm^3]}*200[cm^3]
$$
加えた水の質量が
$$
\frac{1.00g}{[cm^3]}1380[cm^3]
$$
であるため、希釈後のH₂SO₄aq全体の質量は上の二つの式の和である。
求めるH₂SO₄aqの体積はそれに密度で割れば良いので、求めるH₂SO₄aqの体積は
$$
(1.84*200+1380)[g]*\frac{[cm^3]}{1.12[g]}
$$
$$
=1560≒1.56*10^3
$$
よって求める値は
加えた水の体積は1.38*10^3[cm^3]
得られるH₂SO₄aqの体積は1.56*10^3[cm^3]
問題文で与えられている値は全て有効数字3桁で記述されているので、どんな計算をしても必ず有効数字3桁で答えてください。
では、最後の問題です。
密度1.20g/cm^3,濃度33.0%の硝酸275cm^3に密度1.50g/cm^3,濃度59.0%の硝酸をxcm^3加えたところ、密度1.30g/cm^3,濃度y%の硝酸が600cm^3調製された。このとき、xとyの値をそれぞれ求めよ。ただし、硝酸の分子量を63.0、水の密度を1.00g/cm^3とする。
行き詰まったら、図を描いたら何かに気づくかもしれません。
実際に図を書いたものがこちらになります。

HNO₃aqの質量は保存しているから、HNO₃aqについて等式を立てると、
$$
275[cm^3]*\frac{1.2[g]}{[cm^3]}+x[cm^3]*\frac{1.5[g]}{[cm^3]}=600[cm^3]*\frac{1.3[g]}{[cm^3]}
$$
$$
x=\frac{1.3*600-1.2*275}{1.5}
$$
$$
x=300
$$
また、HNO₃について立式すると
$$
275[cm^3]*\frac{1.20[g]}{[cm^3]}*\frac{33}{100}+300[cm^3]*\frac{1.5[g]}{[cm^3]}*\frac{59}{100}=600[cm^3]*\frac{1.3[g]}{[cm^3]}*\frac{y}{100}
$$
$$
\frac{275*1.20*33+300*1.5*59}{1.3*600}=y
$$
$$
y=48.0
$$
したがって求める値は
x=300,y=48.0
(xとyの値を求めよと聞かれているから、こう答えるのが無難)
最後に
今回の記事は作るのに時間がかかりすぎて丁寧さに欠けたような気がします。
もしこの点イマイチよく分からなかったなどあればコメントで教えてください!
良ければスキを押していただけると助かります!
