
マクドナルドの値段の決め方を予測する【pythonで重回帰分析】McDonald's
McDonald's Japan
チーズバーガー、ポテトにナゲット。
誰からも愛される、世界のジャンクフードの帝王。

私も大好きです。
食べている最中に得る【ドーパミン】と引き換えに受け取る、食後の罪悪感。
太るし、体に悪い。
しかし、構わん❕
カモン!!コレステロール❕
て、感じで今、フィレオフィッシュとナゲットとポテトを食べています。
ところで、皆様マクドナルドで一番高いメニューって何か知っていますか?
なんと、『ポテナゲ特大』なんです。

バーガー類じゃないんだ~(・ω・)ノ
ナゲポヨと思いながら、
「マクドナルドってどうやってメニューの値段を決めているんだ❕❓」
と感じたので、商品価格予測モデルを作って見ました。
❶マクドナルドの半分はビタミンと重さでできている
お察しの通りです。
そーなんです。
マクドナルドはビタミンと製品重量が重要なんです。

「… 何を言っているのか わからねーと思うが おれも 何をされたのか わからなかった… 」
御託はこれくらいにして、データを見ていきましょう(・ω・)ノ
マクドナルドはHP上で、下図のようなデータ一覧表を掲示しています👇

このデータはスクレイピングするまでもないので、コピペでエクセルを作成しました。それをCSVとして加工したデータを下記に置いておきます。
このファイルを使って、
【栄養情報一覧】から【メニューの値段を決めている要素】を探し出します。
まずは、Googledriveに上記ファイルをアップロードし、CSVにアクセス。データの中身を確認👇
データは2021.6.18時点のものです。
※バーガーメニューとサイドメニューのみデータ化しており、ドリンクとマックカフェバイバリスタは含んでおりません。
# @title Colab から Google Drive を使う(Google Drive のスペースをマウント)
from google.colab import drive
drive.mount('/content/drive')
import numpy as np # 数値計算
import pandas as pd # データフレーム操作
from sklearn import linear_model # 機械学習の線形モデル
from sklearn.preprocessing import StandardScaler # 標準化
# データセットの読み込み 日本語が入っているcsvファイルは、UTF-8では読めないからShift_JIS に変更(encoding=)
df = pd.read_csv('/content/drive/My Drive//mac.csv', encoding="shift-jis")
df
とりあえず、カロリーの高い順と、値段の高い順に並べてみます。
ポテトやナゲットの大きいサイズが目立ちます(・ω・)ノ👇
# カロリーでソートし、デブまっしぐらのメニュー上位5位を表示
debu = df.sort_values(by = "エネルギーkcal",ascending=False)
debu.head(5)
# 値段でソートし、お財布に厳しいメニュー上位5位を表示
price = df.sort_values(by = "値段",ascending=False)
price.head(5)
何となく、懐かしのエビちゃんを探してみましょう(・ω・)ノ
何故、イルマリ如きと結婚してしまったのか?ま、いーや👇
# えびちゃんを探せ!
df.query('商品名.str.contains("えび")', engine='python')
続いて、基本統計量です👇
# 各列の要約統計量を取得
df.describe()
値段の平均値は298円。最高値は800円。最安値は30円👇

さて、データの概要が分かってきたところで、
【メニューの値段を決める要素が何なのか?】を探っていきます👇
df1 = df.drop(['商品名'], axis=1)
# 標準化
scaler = StandardScaler()
scaler.fit(np.array(df1))
df_std = scaler.transform(np.array(df1))
df_std = pd.DataFrame(df_std,columns=df1.columns)
# 目的変数(Y)
Y1 = np.array(df_std['値段'])
# 説明変数(X)
# 説明変数のみ抽出して変数Xに格納
X1 = df_std.loc[:, '製品重量g/個':'食塩相当量g']
print("標準化後の説明変数X1-----------\n{}".format(X1))
print("標準化後の目的変数Y1-----------\n{}".format(Y1))
# 線形モデルのインスタンスを生成
model = linear_model.LinearRegression()
# データを渡してモデルを生成
model.fit(X1,Y1)
# 係数の値を取得し、変数coefficientに格納
coefficient = model.coef_
# カラム名とインデックス名を付与してデータフレームに変換
df_coefficient = pd.DataFrame(coefficient, columns=["標準化偏回帰係数"], index=[X1.columns])
print(df_coefficient)
# statsamodelでP値 t値をチェック
import statsmodels.api as sm
x_add_const = sm.add_constant(X1)
model_S = sm.OLS(Y1, x_add_const).fit()
print(model_S.summary())扱う単位がkcal、g、mgと異なる重回帰分析の為、説明変数を標準化👇
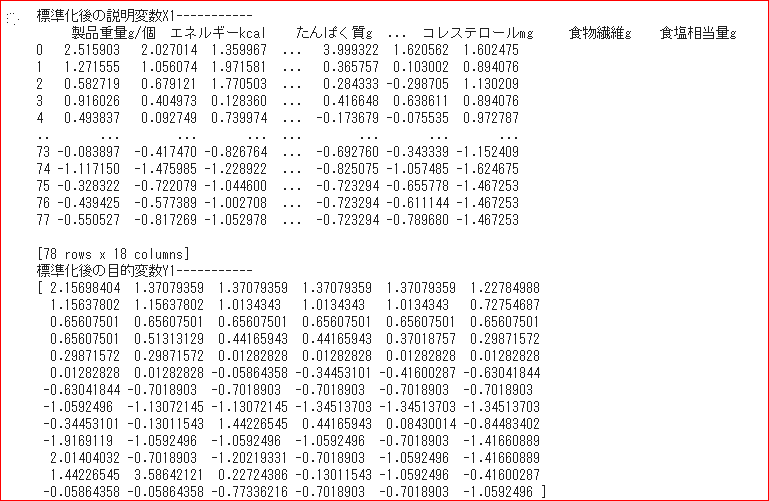
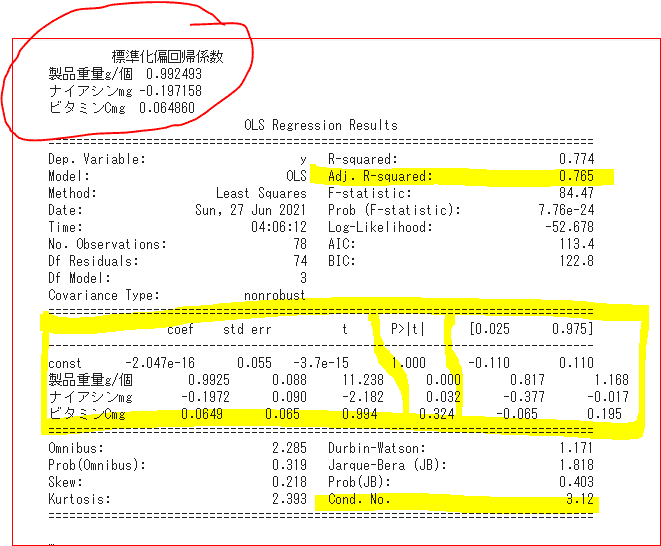
偏回帰係数を見てみますと、「脂質・炭水化物・ナトリウム」がメニューの値段に影響しているように見えますが、t値とp値をみて、本当にその偏回帰係数に有意があるのか確認して見ます👇

結果は、「脂質:0.487 ・炭水化物:0.594 ・ナトリウム:0.408」と、p値が高すぎて、当てにならない為、p値が0.1以下である、偏回帰係数「製品重量・ナイアシン・ビタミンC」に焦点をあてました。👇
※ナイアシンは水に溶ける水溶性ビタミンのひとつで、ビタミンB群の仲間です。ナイアシンはニコチン酸とニコチンアミドの総称ですが、体内でトリプトファンという必須アミノ酸からも合成することができ、私たちはこれらをナイアシンとして利用しています。=ビタミン

これら「製品重量・ナイアシン・ビタミンC」以外の係数は除外し、再度重回帰を行います👇
# p値が0.1以上の説明変数を除外
Z = df_std[['製品重量g/個', "ナイアシンmg", "ビタミンCmg"]]
Y1 = Y1 # 目的変数
# データを渡してモデルを生成
model.fit(Z,Y1)
# 係数の値を取得し、変数coefficientに格納
coefficient = model.coef_
# カラム名とインデックス名を付与してデータフレームに変換
df_coefficient = pd.DataFrame(coefficient, columns=["標準化偏回帰係数"], index=[Z.columns])
print(df_coefficient)
x_add_constant1 = sm.add_constant(Z)
result = sm.OLS(Y1, x_add_constant1).fit()
print(result.summary())ここで、各偏回帰係数の要素ごとに、上位10位メニューを見ていきましょう(^_-)-☆
1.製品重量:0.992(製品重量が重いほど、値段が上がります)
特徴として、ポテト関連を含むシェアポテトやポテナゲ特大・大が上位 にきてます。ま、重量なので、当然ですね。
その結果、標準化偏回帰係数は、
『製品重量:0.992 ・ナイアシン:△0.197 ・ビタミンC:0.064』という偏回帰係数を得ました。
自由度調整済み決定係数:0.765(76%)
Cond. No:3.12(多重共線性低い)
ここで、各偏回帰係数の要素ごとに、上位10位メニューを見ていきましょう(^_-)-☆
1.製品重量:0.992(製品重量が重いほど、値段が上がります)
特徴として、ポテト関連を含むシェアポテトやポテナゲ特大・大が上位 にきてます。ま、重量なので、当然ですね。
# 製品重量g/個上位10位を表示
a = df.sort_values(by = "製品重量g/個",ascending=False)
a.head(10)
2.ナイアシン:△0.197(※係数がマイナスなので、ナイアシンが多いほど、値段が下がります)
特徴として、ヨーグルトやサイドサラダなどのヘルシー系が下位を占めます。上位は相変わらずポテト関連です。
# ナイアシンmg/個上位10位を表示
c = df.sort_values(by = "ナイアシンmg")
c.head(10).append(c.tail())
3.ビタミンC:0.064(ビタミンCが多いほど、値段が上がります)
特徴として、ここでもポテト関連を含むシェアポテトやポテナゲ特大・大が上位を占めます。ミニオンもびっくりです。

ここで、標準化偏回帰係数『製品重量:0.992 ・ナイアシン:-0.197 ・ビタミンC:0.064』を
標準化前の偏回帰係数に戻すと、
製品重量:1.542 ・ナイアシン:△5.118 ・ビタミンC:1.129
となります。
重回帰式は下記の通りなので、

計算すると(wi=偏回帰係数、xi=メニューごとの値)、
マクドナルドのメニューの値段の決め方は、
製品重量×1.542 + ナイアシン×△5.118 + ビタミンC×1.129
で説明できる❕と言えそうです(^_-)-☆
そして、その正解率は76%の精度を持ちます。
次回から、新メニューが発表されたら、重さとビタミンで値決めしたな❕❓(ΦωΦ)フフフ…とか、思って下さい
(* ̄▽ ̄)フフフッ♪
※例 シェアポテト 500円
製品重量340g×1.542 + ナイアシン12.5mg×△5.118 + ビタミンC40mg×1.129 = 505.7円
各メニューの実際の価格と予測価格👇

また、価格を形成する係数要素から見ると、主要な商品はバーガー類ではなく、ポテトこそがマクドナルドを支える主力商品ということも分かりました❕( ..)φメモメモ
ようやく帰結です。
マクドナルドの半分はビタミンと重さでできていました。
詳細は、ビタミンCとナイアシン(水溶性ビタミン)と重量(ボリューム)でした。
あと半分はスマイルでいいでしょう。。。。(*ノωノ)
❷pythonコード
# @title Colab から Google Drive を使う(Google Drive のスペースをマウント)
from google.colab import drive
drive.mount('/content/drive')
import numpy as np # 数値計算
import pandas as pd # データフレーム操作
from sklearn import linear_model # 機械学習の線形モデル
from sklearn.preprocessing import StandardScaler # 標準化
# データセットの読み込み 日本語が入っているcsvファイルは、UTF-8では読めないからShift_JIS に変更(encoding=)
df = pd.read_csv('/content/drive/My Drive//mac.csv', encoding="shift-jis")
df
# カロリーでソートし、デブまっしぐらのメニュー上位5位を表示
debu = df.sort_values(by = "エネルギーkcal",ascending=False)
debu.head(5)
# 値段でソートし、お財布に厳しいメニュー上位5位を表示
price = df.sort_values(by = "値段",ascending=False)
price.head(5)
# えびちゃんを探せ!
df.query('商品名.str.contains("えび")', engine='python')
# 各列の要約統計量を取得
df.describe()
df1 = df.drop(['商品名'], axis=1)
# 標準化
scaler = StandardScaler()
scaler.fit(np.array(df1))
df_std = scaler.transform(np.array(df1))
df_std = pd.DataFrame(df_std,columns=df1.columns)
# 目的変数(Y)
Y1 = np.array(df_std['値段'])
# 説明変数(X)
# 説明変数のみ抽出して変数Xに格納
X1 = df_std.loc[:, '製品重量g/個':'食塩相当量g']
print("標準化後の説明変数X1-----------\n{}".format(X1))
print("標準化後の目的変数Y1-----------\n{}".format(Y1))
# 線形モデルのインスタンスを生成
model = linear_model.LinearRegression()
# データを渡してモデルを生成
model.fit(X1,Y1)
# 係数の値を取得し、変数coefficientに格納
coefficient = model.coef_
# カラム名とインデックス名を付与してデータフレームに変換
df_coefficient = pd.DataFrame(coefficient, columns=["標準化偏回帰係数"], index=[X1.columns])
print(df_coefficient)
# statsamodelでP値 t値をチェック
import statsmodels.api as sm
x_add_const = sm.add_constant(X1)
model_S = sm.OLS(Y1, x_add_const).fit()
print(model_S.summary())
# p値が0.1以上の説明変数を除外
Z = df_std[['製品重量g/個', "ナイアシンmg", "ビタミンCmg"]]
Y1 = Y1 # 目的変数
# データを渡してモデルを生成
model.fit(Z,Y1)
# 係数の値を取得し、変数coefficientに格納
coefficient = model.coef_
# カラム名とインデックス名を付与してデータフレームに変換
df_coefficient = pd.DataFrame(coefficient, columns=["標準化偏回帰係数"], index=[Z.columns])
print(df_coefficient)
x_add_constant1 = sm.add_constant(Z)
result = sm.OLS(Y1, x_add_constant1).fit()
print(result.summary())
# 切片を取得
print("切片: {}".format(model.intercept_))
# 決定係数を取得
print("決定係数: {}".format(model.score(Z, Y1)))
# 製品重量g/個上位10位を表示
a = df.sort_values(by = "製品重量g/個",ascending=False)
a.head(10)
# ナイアシンmg/個上位10位を表示
c = df.sort_values(by = "ナイアシンmg")
c.head(10).append(c.tail())
# ビタミンCmg/個上位10位を表示
b = df.sort_values(by = "ビタミンCmg",ascending=False)
b.head(10)
y = df[['値段']]
x1 = df[['製品重量g/個']]
x2 = df[['ビタミンCmg']]
from mpl_toolkits.mplot3d import Axes3D #3Dplot
import matplotlib.pyplot as plt
import seaborn as sns
fig=plt.figure()
ax=Axes3D(fig)
ax.scatter3D(x1, x2, y, label='Dataset')
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("y")
plt.show()❸Facebookが開発した機械学習ライブラリで株価を予測
pythonで株価分析⑦【Facebookが開発した機械学習ライブラリで株価を予測する】
機械学習で、日本マクドナルドHDの今後の株価を予測して見た。
・対象銘柄:日本マクドナルドHD 銘柄コード:2702
・学習期間:2016.7.2~2021.7.1(5年間)

現在(2021.7.2時点)の株価が100株:4,910円なのに対して、1年後は100株:4,500円付近まで下落する予測ですね(・ω・)ノ

東京オリンピックも終わっていることだし、テーパリングも余裕で始まっているはず❓なので、かなり妥当な予測と言えるかもしれません(*‘ω‘ *)
私の5,000円で購入した含み損を助けてあげて下さい(´・ω・`)
では、ばいちゃ
(*´▽`*)
e^iπ + 1 = 0
