フォワードテストシリーズ第二回 〜パラメータ最適化と優位性の評価〜
こんにちは、minaulです。
前回の記事にて、フォワードテストの概要についてざっくりとお話ししました。
今回は、フォワードテストを実行する前段階として、バックテストのパラメータ最適化を通して、サンプルデータの準備をしてみましょう。
パラメータ最適化とは
パラメータ最適化とは、バックテストのパフォーマンス結果が特定期間において良好に適合するために、投資モデルの可変パラメータを変更することです。
このパラメータ最適化を行う手法として、感覚による手動埋めによって適したパラメータを発見する方法*もあります。
* データ分析関連の上級者などに限っては、豊富な経験知によって手動でのパラメータ設定・探索も十分ありうるようです。(複雑なモデルに対しての計算コストの削減による効率化などのメリットがある)
しかし、経験知がないという場合、手動での探索はかなりのコストを要すると想定されます。(もちろん、単純にダメということではないです)
こういう時は、プログラミングの技術を使うことで、複数のパラメータ探索を自動化することができます。
この複数探索は、データへの理解度が低い場合(ここでは投資モデルの実力が分からないなど)、視覚的な理解に役立ってくれます。
今回はシンプルなモデルを使うため、自動化しても大きな計算コストを要しないことから、別途コードを書いて自動パラメータ探索を行います。
記事の最後にコードも置いています。
最適化期間
みなさん、むやみにバックテストを行なっていませんでしょうか。
かくいう私も、結構適当というかアバウトな感覚でバックテストを回しておりました。
ただ、前回の記事でも触れた通り、フォワードテストの存在を考慮するならば、バックテストにかかる最適化期間も厳密に定義しなければなりません。
今回は最もシンプルなフォワードテストを前提に置くことにします。
その上で、最適化期間などの基本設定は以下で統一します。
パラメータ最適化期間:3ヶ月
(↑=バックテスト期間)
フォワードテスト期間:1ヶ月
* 時間軸は1時間足で検証
このように、学習データと検証データを分ける必要があります。
学習データと検証データの比率は9:1や8:2などが一般的なようです。
本番用に計算する場合は、統計的信頼性などの観点から、全体的に期間をさらに長く取る必要があるでしょう。
今回はサンプルなので、短い期間で検証することにします。
優位性の確認
バックテストを行う最大の目的は、投資モデルの優位性を確認することです。
そして、パラメータ最適化もといパラメータ探索を通して、優位性の存在とそのレベル感を測っていきます。
過去データとはいえ、市場に対して優位性を確認できることは、投資戦略策定の中で大きな一歩と言えるでしょう。
ではパラメータ探索を行い、どのような判断を持って優位性を確認・評価すればいいでしょうか。
ここでは一例として、完全にランダムな売買シグナルによる投資モデルには果たして優位性があるのか、バックテストによって検証してみます。
直感的には、ランダムな投資戦略などに優位性などないように感じてしまいます。
なぜならば、その投資モデルのロジック自体を理論的に説明することが到底できないからです。
ランダムな例として、以下の投資モデルを定義します。
まず始めに目が0〜9のサイコロを振ります。
例えば"4"が出たら、その値を"出目"とします。
エントリーシグナル:終値の一の位が出目と一致する
エグジットシグナル:終値の一の位が出目と一致する
最初に振ったサイコロの出目に加え、一の位という価格との関連性がほぼ皆無な指標の組み合わせによって、投資モデルが決定してしまうという、ランダム性の高いモデルとなっています。
ここでの可変パラメータは、サイコロの出目になります。
ともあれ、この投資モデルをバックテストして、パラメータ探索を行ってみましょう。
ちなみに前提条件として、初期資金100万円、全て成行のルールにしています。
代表的な成績指標をまとめたdataframeは以下の通りです。

最大ドローダウン率、プロフィットファクター、運用成績、最終資金
上のバックテスト結果を見ると、出目が3の時の成績が際立っていますね。
PF1.4に加え、たった3ヶ月で運用成績が220%超えです。これは素晴らしい成績と言っても過言ではありません。
ただし、このロジックを実運用に投入しようという方は果たしているでしょうか。
この時点では、ランダムな影響を受けた結果たまたま成績が良かったのか、それとも終値の一の位が3の時に本当に市場に対して優位性を持っているのか、判断できません。
こういう時に、フォワードテストを使うことで、ロバストな優位性か否か見極めることができるのです。
次回の記事にて実際に検証したいと思います。
さて、パラメータ最適化によって、出目が3のときに最も成績が良くなることが分かりました。
それと同時に、この投資モデル自体に優位性が存在するのかを確認してみましょう。
出目と運用成績をプロットした図を以下に示します。
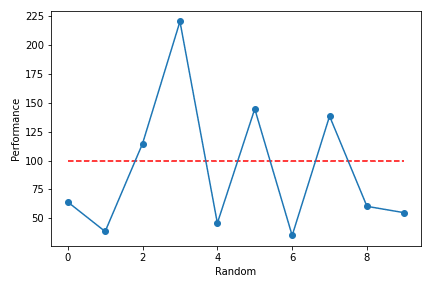
見事なまでにジグザグな形状をしていることが分かります。
このように、パラメータの連続的変化によって、投資モデルの成績に連続性が確かめられない場合は、不確実なモデルである可能性が高くなります。
しかし、この可視図を見ただけでは、投資モデルに優位性が存在するのか、分かりかねませんか?
と言うことで統計値を見てみると、運用成績の平均が91.66%、標準偏差が57.76%ですが、やはりこれだけではいまいち判断がつきません。
ここでは、統計学的手法として、t検定を試してみます。
t検定
t検定は仮説検定の手法のうちの一つです。
仮説検定とは、ある仮説について成否を判断する方法です。成否の根拠には確率が用いられ、その確率が閾値を越える場合のみ「正しい」と認めることができます。
t検定とは、t分布を使った仮説検定です。
t分布は、最も一般的な分布である正規分布に対して、その母分散が未知である場合に活用することができます。
t検定で何を検証したいか、統計学的に言えば「1標本の平均の検定」です。
噛み砕いて言えば、「一部データから得たサンプルモデルを、擬似的に"本来の"投資モデルとして扱った上で、成績が平凡で優位性のない投資モデルと比較して、運用成績の平均に差があるか否か(=上回るか否か)」を検証したいのです。
また、t検定は少ないサンプルデータに対しても利用できるという大きな強みを持っています。
今回のように、パラメータの候補サンプル数が0〜9の10個しかない場合でも適用が可能です。
t検定の具体的な手順は以下の通りです。
1. 帰無仮説・対立仮説を立てる
2. 有意水準を設定する
3. t値を算出する
4. p値を算出する
5. p値と有意水準を比較する
6. 帰無仮説を棄却する/しない
今回の帰無仮説は、「運用成績の平均が100%である」こととします。
対立仮説は、「運用成績の平均が100%を上回る」とします。
この帰無仮説を片側検定で棄却できれば、投資モデルに一定の優位性があると認められます。
どういうことかと言うと、運用成績平均が100%であることの確率が上側に十分に小さい、すなわち平均的な運用成績が100%を上回ると見込めるわけです。
有意水準は一般的な「5%」に設定します。ちなみに、結果を見た後からこの数値を弄り回す行為は絶対に避けましょう。仮説検定を行う意味がなくなります。
t値は「比較するデータに意味のある差があるかどうか」を示す値です。
p値は「得られたデータの希少性」を示す値で、t値が求まれば自然に決定します。
t値の計算式を簡単に説明します。
$$
\begin{array}{}T = \frac{\bar{x}-\mu}{\sqrt{ \frac{s^2}{n}}}\sim{t_{(n-1)}}\end{array}
$$
数学的に言えば、t値は既知・未知の平均と、不偏分散によって計算されます。
数式の〜とは、t値が自由度n-1のt分布に従っているということです。
サンプル例の場合は、自由度9となります。
t値もp値も今時便利な統計ソフトがたくさんあるので、さくっと計算が可能です。
そして、p値と有意水準を比較して、p値が有意水準を下回る場合、仮説が起こる確率が十分に小さいとして、帰無仮説を棄却することができます。
つまり、対立仮説が正しいと統計的に立証できるのです。
計算の結果、t値が-0.433、p値が0.662となりました。
結果を見る限り、p値が有意水準を余裕で上回っているので、帰無仮説を棄却することはできません。グラフに描画してみましょう。

赤線で示したt値は、上側の5%範囲には全くかすりもしていません。
ということで、このランダムな投資モデルには優位性があるとは言えない、と結論付けられます。
とはいえ、パラメータ最適化で得た出目が3の時の投資モデルについては、最終の運用成績を見る限り、優位性があると思えませんか?
単一のストラテジーの優位性を評価する場合は、時系列リターンを使うのが一般的なようです。
時系列リターンに対して、同様にt検定を行ってみましょう。
パラメータ最適化時の時系列リターンのデータ数(=トレード回数)が200、平均は0.37、標準偏差は2.38でした。
帰無仮説を「平均リターンが0である」と設定し、有意水準を5%としてt検定にかけます。
計算の結果、t値が2.162、p値が0.016でした。
グラフに描写すると以下の通りです。

図を見て分かる通り、今度はt値がしっかりと上側5%区間に収まっています。
これはつまり、「平均リターンが0である」ことの確率が十分に低いことを意味しています。
ということで、帰無仮説を棄却できるため、出目が3の時のストラテジーには優位性がある、と結論づけられます。
t検定を以て検証を終えてもいいのですが、ここではもう一歩踏み込んだ考えとして、さらにp平均法を紹介します。
p平均法
仮想通貨Bot界隈に明るい方はご存知の方もいらっしゃるかと思います。
このp平均法という概念は、有名Botterであるrichmanbtcさんが考案された指標です。
p平均法は、データを分割して複数回p値を計算することで、その平均値によってt検定を行う手法です。
具体的な手順は以下の通りです。
1. リターン時系列をN個の期間に分割
2. 各期間でt検定してp値を計算する
3. 得られたN個のp値の平均を取る
4. mean(p)が有意水準を下回れば優位性を認める
この手法の利点は、従来の単純なt検定と比して、期間によらず安定的なリターンへの評価を重視できる点です。
また、偽陽性(本当は有意でないのに有意と出てしまう統計的誤り)の確率を、分割数を増やすほど、ほぼ無視できるレベルまで小さくすることができます。
ただし、小さく負けて大きく勝つようなトレンドフォロー型の投資モデルの場合、時系列リターンにばらつきが生じるため、p平均法では上手く評価できないかもしれません。
先ほどのパラメータを最適化したランダムモデルで、p平均法を試してみましょう。
今回は、半月ごとに分割して、N=6個の期間で計算します。
各期間のp値は、0.066, 0.869, 0.252, 0.459, 0.018, 0.453 でした。
p平均値は0.353となり、有意水準を上回るため、帰無仮説は棄却できません。
ということで、よりロバストに厳密な検証手法を使った結果、出目3のストラテジーであっても、優位性は認められませんでした。
* 以下、個人的な検証の過程を載せていますが、余談ですので飛ばしていただいても結構です。
もう少し試してみてN=3の場合(1ヶ月分割)、p平均値は0.192でした。
分割のNによって、確かにp平均値の厳密性は変わるようです。
ただし、このp平均法の場合は、相当厳しい条件をクリアしなければ、優位性を確認できないため、偽陰性(本当は有意なのに有意でないと出てしまう統計的誤り)の確率がかなり高いような気がします。
参考までにパラメータ最適化ランダムモデルの資産推移と時系列リターン分布を載せておきます。

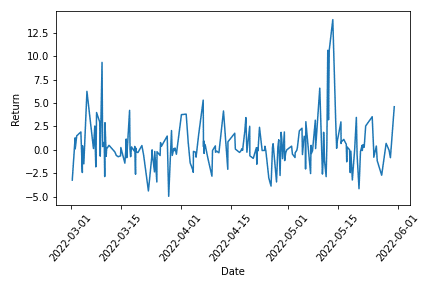
横軸のDateがちょうど6分割されているので、先ほどの各期間のp値と比較してみると、資産がマイナスになっているのは当然として、資産が横ばい(微増)の期間であっても、p値はかなり高い値を示してしまっています。
この主な原因としては、時系列リターンの分散の高さが挙げられます。
p値(t値)の計算には分散が用いられているため、平均値が正でも分散(標準偏差)が高い場合は、p値も高く出てしまう傾向があります。
以上から、p平均法で優位性を確認するためには、リターン分布が低ボラティリティ、かつ平均値が全期間で高水準である必要があります。
となれば、必然的にp平均法で検証すべき戦略スタイルは、スキャルなどの高頻度に絞られるような気がします。
スイングなどの損小利大にエッジを持つ戦略の場合は、p平均法によってその優位性を適切に測れるのか疑問が残ります。
また高頻度であっても、p平均法で良好な結果を得るためには、上記のリターン分布の特性を満たす必要があり、その場合資産推移は綺麗な右肩上がりを描くであろうことは容易に想像できます。
つまり、p平均法のようなロバスト性の高い検証手法で、優位性の確証を得るには、相当高いハードルが存在します。
以上、筆者の雑感でした。
公開コード
最後に今回の検証に用いたコードを公開します。
パラメータ探索を自動化するコードですが、こちらの記事のコードを前提にしているため、詰まる場合は参考にしてください。
上記の記事の"共通ロジック"に格納する、パラメータ最適化のためのバックテスト関数を始めに説明します。
# パラメータ最適化用のバックテスト関数
def backtest_optimize():
# 成績を記録したPandas DataFrameを作成
records = pd.DataFrame({
"Date" : pd.to_datetime(flag["records"]["date"]),
"Profit" : flag["records"]["profit"],
"Side" : flag["records"]["side"],
"Rate" : flag["records"]["return"],
"Stop" : flag["records"]["stop-count"],
"Periods" : flag["records"]["holding-periods"],
"Slippage" : flag["records"]["slippage"]
})
# テスト日数を集計
time_period = datetime.fromtimestamp(last_data[-1]["close_time"]) - datetime.fromtimestamp(last_data[0]["close_time"])
time_period = int(time_period.days)
# 総損益の列を追加する
records["Gross"] = records.Profit.cumsum()
# 資産推移の列を追加する
records["Funds"] = records.Gross + start_funds
# 最大ドローダウンの列を追加する
records["Drawdown"] = records.Funds.cummax().subtract(records.Funds)
records["DrawdownRate"] = round(records.Drawdown / records.Funds.cummax() * 100, 1)
# バックテストの計算結果を返す
result = {
"トレード回数" : len(records),
"勝率" : round(len(records[records.Profit > 0]) / len(records) * 100, 1),
"平均リターン" : round(records.Rate.mean(), 2),
"最大ドローダウン率" : -1 * records.DrawdownRate.loc[records.Drawdown.idxmax()],
"プロフィットファクター" : round(-1 * (records[records.Profit>0].Profit.sum() / records[records.Profit<0].Profit.sum()), 2),
"最終損益" : records.Profit.sum(),
"運用成績" : round(records.Funds.iloc[-1] / start_funds * 100, 2)
}
return result
説明記事内のbacktest関数と大差ないですが、最後にresultという結果を集計した配列を返しています。
次に戦略ロジックとメイン処理の部分を全て記します。
ちなみに今回はドテン売りを加えているので、メイン処理の使用関数がentry_signal_dotenなど別で独自に関数を定義していますが、本質的ではないしコードが長くなるのでここでは割愛します。
# -----------パラメータ設定---------------
random_list = [i for i in range(0,10,1)] # 0〜9の配列作成
# ------------ロジックの個別部分-----------------
# ランダムのエントリーシグナルを判定する関数
def logic_signal():
# エントリーサイン:一の位がランダム数字と一致(売買条件が同じのため少し加える)
if str(data["close_price"])[-1] == str(random) and flag["position"]["side"] == "SELL":
return {"side":"BUY", "price":data["close_price"]}
# エグジットサイン:一の位がランダム数字と一致
if str(data["close_price"])[-1] == str(random):
return {"side":"SELL", "price":data["close_price"]}
return {"side":None, "price":0}
# -----------ここからメイン処理--------------
# 価格チャートを取得
price = tool.get_price(3600, before=1654005600, after=1646060400)
# テストごとの各パラメーターの組み合わせと結果を記録する配列を準備
param_random = []
result_count = []
result_winrate = []
result_returnrate = []
result_drawdownrate = []
result_profitfactor = []
result_performance = []
result_gross = []
# 総当たりのためのfor文の準備(今回は可変パラメータが1つだが、複数探索の場合はここに追加)
combinations = [(random)
for random in random_list]
# パラメータごとにメイン処理
for random in combinations:
# フラグ変数
flag = main.flags()
need_term = 0
last_data = []
i = 0
# メインのループ文
while i < len(price):
data = price[i]
if flag["order"]["exist"]:
flag = enex.check_order(flag)
if flag["position"]["exist"]:
flag = enex.close_position_doten(flag)
else:
flag = enex.entry_signal_doten(flag)
last_data.append(data)
i += 1
time.sleep(wait)
result = back.backtest_optimize()
# 今回のループで使ったパラメータの組み合わせを配列に記録する
param_random.append(random)
# 今回のループのバックテスト結果を配列に記録する
result_count.append(result["トレード回数"])
result_winrate.append(result["勝率"])
result_returnrate.append(result["平均リターン"])
result_drawdownrate.append(result["最大ドローダウン率"])
result_profitfactor.append(result["プロフィットファクター"])
result_performance.append(result["運用成績"])
result_gross.append(result["最終損益"])
# 全てのパラメータによるバックテスト結果をdataframeで1つの表にする
dfr = pd.DataFrame({
"random" : param_random,
"count" : result_count,
"winrate" : result_winrate,
"return" : result_returnrate,
"DDmax" : result_drawdownrate,
"PF" : result_profitfactor,
"performance" : result_performance,
"finalfund" : result_gross
})
print("--------------------------")
print("テスト期間:")
print("開始時点 : " + str(price[0]["close_time_dt"]))
print("終了時点 : " + str(price[-1]["close_time_dt"]))
print(str(len(price)) + "件のローソク足データで検証")
print("--------------------------")
display(dfr) # dataframeの可視化基本的には、コメント挟んでいるので、そちらを確認下さい。
全体の流れとしてまとめると、以下の通りです。
1. 投資モデルを用意する
2. 探索したいパラメータ候補を用意する
3. パラメータごとにメイン処理を実行
4. パラメータごとにバックテスト結果を記録する
5. すべてのパラメータ探索を終えたら、最終的な結果を集計し出力する
6. 結果からパラメータ最適化を行う
1つのパラメータでの単発バックテストと違って、候補全てのパラメータで複数回バックテストを行い、最後に結果を集計してパラメータ最適化を行う、という流れです。
パラメータごとにループ処理を回すイメージが掴めたら、コード全体の流れも理解しやすくなると思います。
ついでにt検定のコードも載せておきます。
from scipy import stats # ライブラリのインポート
print(stats.ttest_1samp(dfr["performance"], popmean=100, alternative='greater')) # 1標本検定
# 出力結果
Ttest_1sampResult(statistic=-0.4332538251428415, pvalue=0.6624856935832337)最後に
以上、バックテストにおけるパラメータ最適化と優位性の評価に関する記事でした。
短編の記事の予定が、色々詰め込んでいたら結構長めの記事になってしまいました。
実際問題、この議題は投資戦略策定の中でも特に重要で、多くの投資家・投機家にとってはモチベーターな部分でもありますから、長くなるのも致し方ないところではあります。
さて、次回からはいよいよ本番のフォワードテストに移っていきます。
単純なフォワードテスト、そして最も一般的手法とされるウォークフォワードテストを取り上げる予定です。
それでは、お読みいただきありがとうございました。
