動的確率的配送計画に対する強化学習と最適化を合わせた解法
1日のトラックの配送順を決める問題は,配送計画問題として知られている.実際の問題においては,需要の不確実性が無視できない場合がある.典型的な2つのケースをあげておく.
・宅配のラストワンマイルにおける不在確率の考慮
・乗り合いタクシー問題
これらは,応用別に解法を設計する必要があると考えているが,ここではその基礎になる手法を考える.元になるのは,最適化と強化学習(近似動的計画)である.
一部の顧客がランダムに発生する場合を考える.再最適化を行う方法が従来の研究では用いられているが,それでは不十分である.以下の図のように,将来発生する顧客が現時点でいない場合,トラックはデポ(中央のオレンジ色の□)に帰ってしまうが,発生する可能性が高い地点に移動したり,その場で待機する「方策」も考えられる.
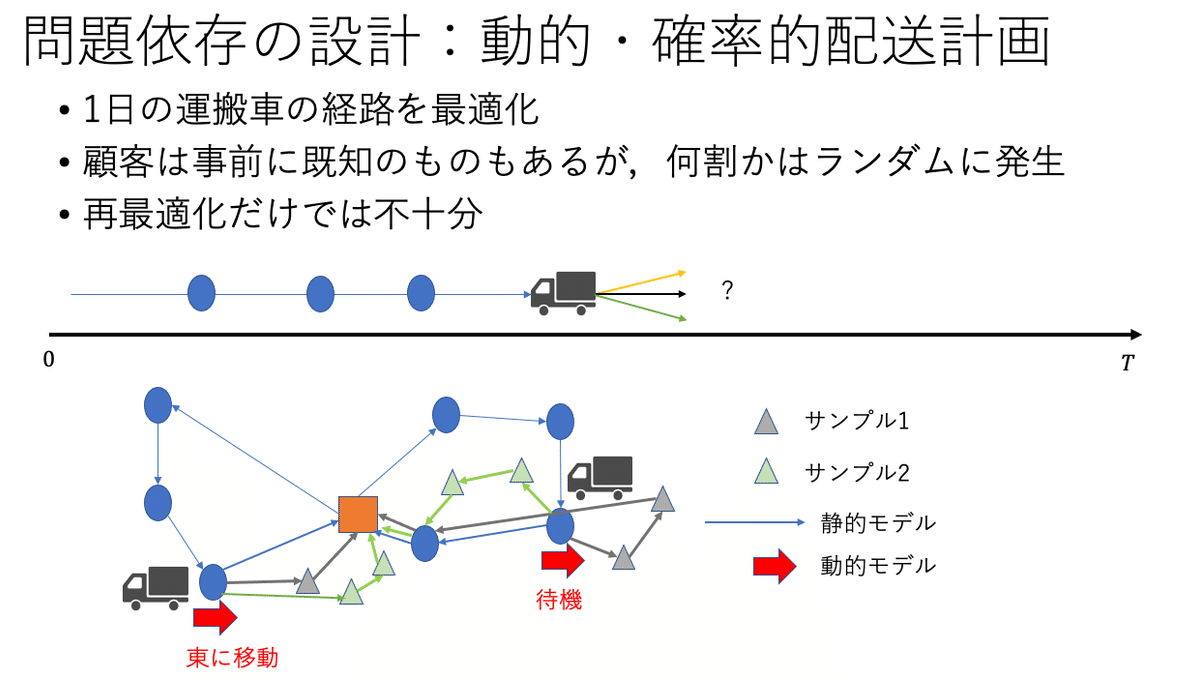
問題は確率的かつ動的なので,単に静的な確定的モデルを解くだけでは不十分で,最適な方策を考える必要がある.
将来事象は徐々に判明してくるので,単に事前に予測をするだけでは不十分である.ここでは,オフライン予測を繰り返し使うことを考える.1日を複数の小区間に分割する.最初の区間の予測には,事前データや外部データを用いたオフライン予測を用い,その後は,その日に収集した新しいデータを用いたオフライン予測を繰り返し行う.

将来発生する顧客は最新の予測に基づいてランダムに発生させる(サンプリング).サンプル毎に現在地点以降のルートを配送最適化ソルバーを用いて解く.これらの複数の解をアンサンブル(多数決もしくは平均)することによって,次の行動を決定するのがコンセンサス法である.

より高度な解法としては,強化学習との融合が考えられる.各運搬車の状態変数を(運搬車の位置,現在時刻,予定ルート,顧客の状態)の組とする.コンセンサス法と同様にサンプリに対してルートを生成し,行動の候補を得たあとで,行動に伴う報酬(マイナスの移動費用)と行動後状態に対する価値関数(の近似)の和を最大にする状態に移動する.その後,新たに発生したランダムな顧客の情報を入れて,行動前状態に移動する.

共同研究をしたい方(もしくは会社)があれば,歓迎します.データを持っていたらなおさら歓迎です.
