
拡散方程式の直感的な意味
更新 2024/12/25
拡散方程式とは, 以下の形で与えられる (2階線形) 偏微分方程式である$${^{*1}}$$. なお, $${\mu}$$ は定数である.
$$
\frac{\partial f (x,t)}{\partial t}=\mu \frac{d^2f (x,t)}{dx^2}
$$
脚注
$${^{*1}}$$簡単のため1次元にしているが, 一般の3次元の場合には以下のように与えられる. また右辺に定数項が付いても良い. そして, このような偏微分方程式の解法は, 変数分離法などが常套手段である.
$$
\begin{equation*}
\begin{split}
\frac{\partial \textbf{\textit{f}} (\textbf{\textit{r}},t)}{\partial t}&=\mu \nabla ^2\textbf{\textit{f}} (\textbf{\textit{r}},t)\\
&\equiv\mu (\frac{d^2}{dx^2}+\frac{d^2}{dy^2}+\frac{d^2}{dz^2}) \textbf{\textit{f}} (\textbf{\textit{r}},t)
\end{split}
\end{equation*}
$$
直感的な意味
結論から言うと, 拡散方程式 $${\frac{\partial f (x,t)}{\partial t}=\mu \frac{d^2f (x,t)}{dx^2}}$$ の両辺について, 以下のようにまとめられる.
ある位置での $${f}$$ の時間変化率が, その周りの平均との差に比例する. そして, その差が小さくなるように $${f}$$ は変化する.
まず, 左辺については簡単なので, 右辺の2階微分について見てゆく. 一旦$${t}$$ 依存性を無視して, ある微少量 $${h (>0)}$$ に対して,
$$
\begin{equation*}
\begin{split} f''(x) &=\lim_{h\rightarrow 0}\frac{1}{h}\{f'(x+\frac{h}{2})-f'(x-\frac{h}{2})\}\\
&\backsimeq\frac{1}{h}\{f'(x+\frac{h}{2})-f'(x-\frac{h}{2})\}\\
&\backsimeq\frac{1}{h}\{\frac{1}{h}(f(x+h)-f(x))-\frac{1}{h}(f(x)-f(x-h))\}\\
&=-\frac{2}{h^2}\{f(x)-\frac{1}{2}(f(x+h)+f(x-h))\}
\end{split}
\end{equation*}
$$
となる$${^{*2}}$$. この式の意味について考えてみよう. $${\frac{1}{2}(f(x+h)+f(x-h))}$$ はその左右 $${x-h, x+h}$$ での関数値の平均になっているので, 今いる位置 $${x}$$ での関数値との差を考えていることになる.
そして, その係数について, $${h^2(\geq 0)}$$ は関係なく, 大事なのはマイナスがついていること. これにより, もし周りの平均値よりも小さかったら $${\frac{\partial f (x,t)}{\partial t}\geq0}$$ となり, $${f(x,t)}$$ は増える向きに時間変化する.

対して, もし周りの平均値よりも大きかったら $${\frac{\partial f (x,t)}{\partial t}\leq0}$$ となり, $${f(x,t)}$$ は減る向きに時間変化する.
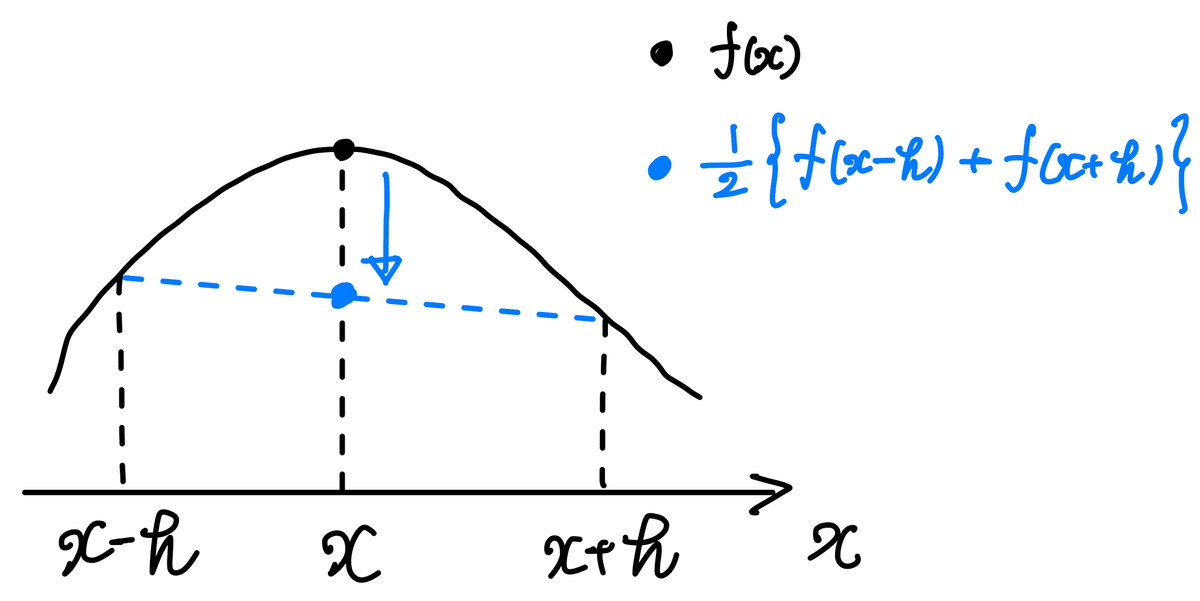
よって, 平均値との差が正負のどちらの場合も, その差が小さくなるような打ち消す向きに時間変化すると言える.
だから, 拡散方程式は, その名の通り時間が経つほど空間的に広がっていく関数が従う方程式なのである.
脚注
$${^{*2}}$$このやり方を差分法という. 本当は2階微分において微少量は $${h, h'}$$ という風に2つ使用しないといけないが, 今回は直感的な議論をしたいだけなので, そのような数学的な厳密性を担保していない.
拡散方程式の例
熱拡散方程式とかが有名で, 例えば以下を参照↓.
また, 量子力学に登場するSchrödinger方程式
$$
i\hbar \frac{\partial\psi(x,t)}{\partial t}=\{-\frac{\hbar^2}{2m}\frac{d^2}{dx^2}+
V(x)\}\psi(x,t)
$$
も拡散方程式の形になっている. 実際, 波動関数 $${\psi(x,t)}$$ の時間発展を追うと, 時間が経つにつれて空間的に広がっていく方程式になっている [2].
文献
[1] 三谷純. "拡散方程式って? ~ラプラシアンの気持ちを理解する~". (2024). (参照 2024/10/28)
[2] J. J. Sakurai, J. Napolitano. 桜井明夫訳.『現代の量子力学 (上)』第2版 (吉岡書店, 2014)
