【熱力学】いろんな熱機関の効率まとめ

2024年9月13日 23:22

更新 2024/12/25

自動車のエンジンなどで知られる「熱機関」の効率についてまとめてみた.

※ なお表記法は田崎熱力学 [1] のものに準ずることにし, 系の平衡状態を, $${(T; V, N) }$$ というように表す.

1. まず熱効率とは？

以下の図1.1のような,

あるサイクル $${C}$$ が, １サイクル$${^{*1}}$$で, 温度 $${T_H, T_L (T_H \geq T_L)}$$ の熱浴と熱エネルギーのやりとりをしながら, 外界へ力学的な仕事 $${W}$$ をする

ものを熱機関heat engineという.

ただし, 同じ仕事 $${W}$$ をするにしても, 受け取った熱 $${Q_H}$$ のうちのほとんどを $${Q_L}$$ として排熱してしまって仕事に変換できない場合, それは熱機関としては良くないということなる. よって, (熱) 効率efficiencyとよばれる,

受け取った熱 $${Q_H}$$ のうち, どのくらいが仕事 $${W}$$ へ変換されたかという割合

$$
\tag{1}\varepsilon\equiv\frac{W}{Q_H}
$$

を導入することで, その熱機関の性能を評価する$${^{*2}}$$. さらに, 熱力学第一法則エネルギー保存則 $${W=Q_H-Q_L}$$ より, (1) 式は書き換えられて

$$
\tag{2} \varepsilon=1-\frac{Q_L}{Q_H}
$$

となる. 以下, この (2) の表式で進める.

$${^{*1}}$$サイクルとは, 平衡状態の系が様々な過程を経たあと, 最終的にはじめの状態に戻ること.
$${^{*2}}$$「≡」とは, 左辺の文字を, 右辺の式で定義するということを表す.

$${p-V}$$ 図で考えると,

となり, 熱浴との熱のやりとりがある (a), (c) の等温準静過程isothermal quasisticと, (b), (d) の断熱準静過程adiabatic quasisticで構成される. 熱効率は,

$$
\tag{3}\varepsilon_0=1-\frac{T_L}{T_H}
$$

と, 熱浴の温度だけで決まり, この効率を超えるエンジンはこの宇宙には存在しないことが知られている.

$${p-V}$$ 図で考えると,

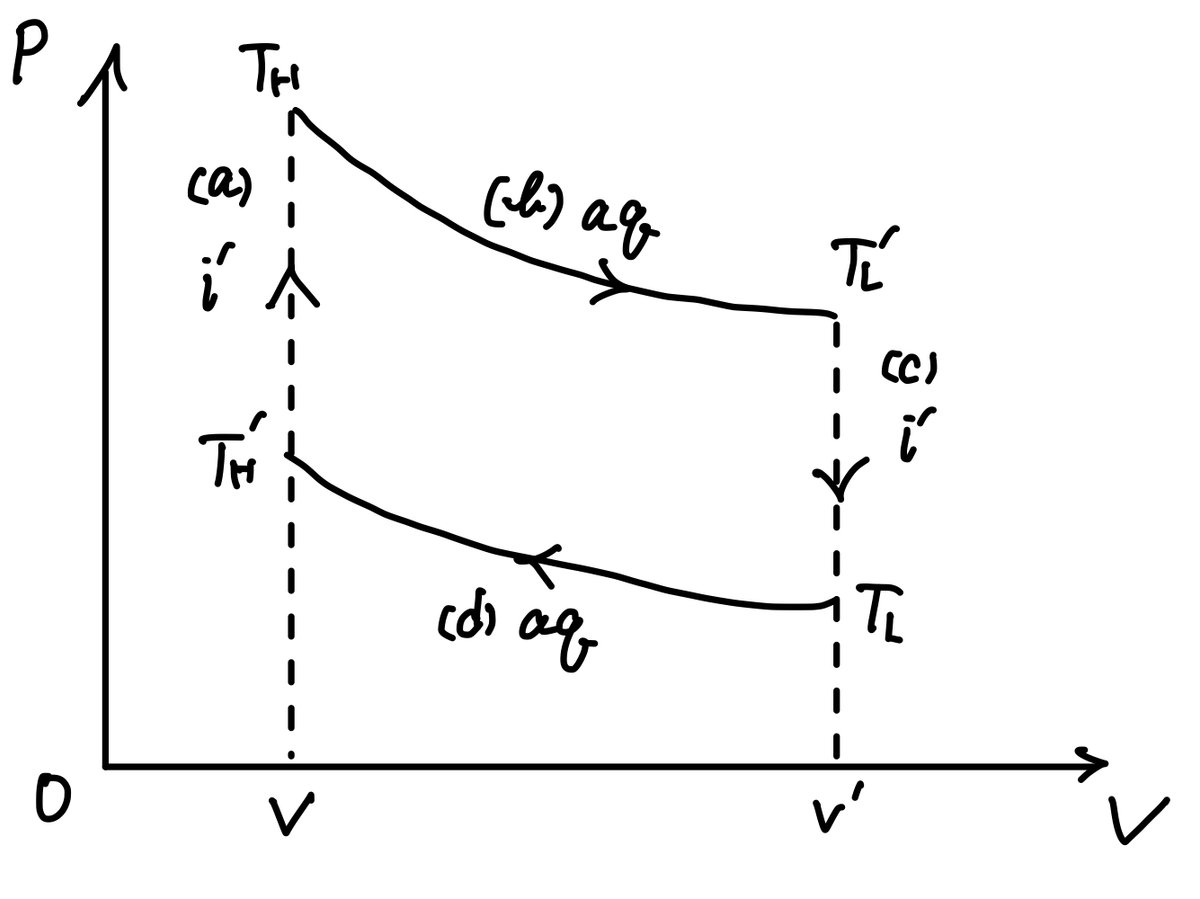
となり, (b), (d) の断熱準静過程adiabatic quasisticと, 熱のやりとりがある (a), (c) の等積過程 (広義の等温過程) で構成される. 熱効率は,

$$
\tag{4}\varepsilon=1-\frac{T_L}{T_H'}
$$

となり, $${T_H'< T_H}$$ より, Carnotサイクルの効率 $${\varepsilon _0}$$ よりは小さくなる.

$${p-V}$$ 図で考えると,

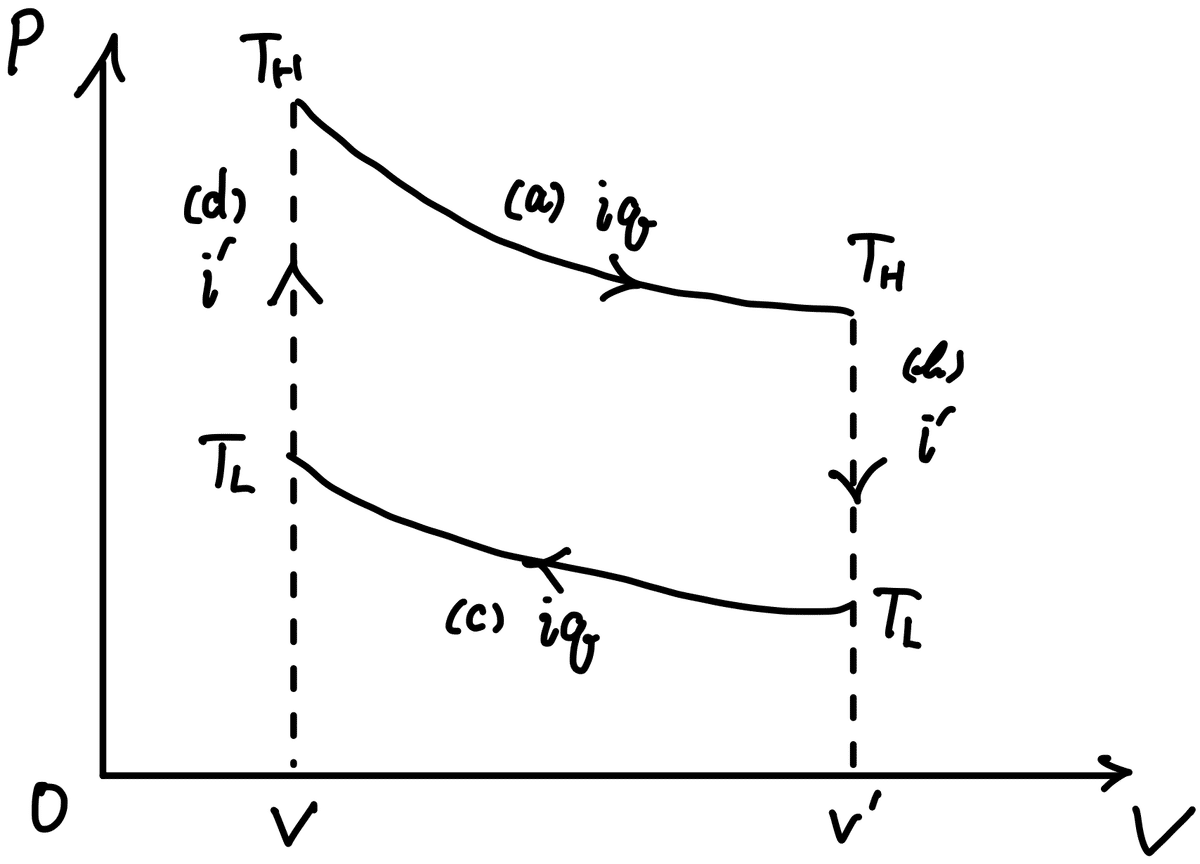
となり, (a), (c) の等温準静過程isothermal quasisticと, (b), (d) の等積過程 (広義の等温過程) で構成される.

どの過程も熱浴と熱エネルギーのやりとりがあるが, 1サイクルにおいて, (b) で一度放出した熱を (d) で吸収されて再利用されることで, 実質 (b), (d) における熱エネルギーのやりとりを無視できるのが特徴. 熱効率は,

$$
\tag{?}\varepsilon=1-\frac{T_L}{T_H}=\varepsilon_0
$$

と, Carnotサイクルの効率と一致する！よって, この結果から分かることは,

最大効率 $${\varepsilon_0}$$ になる熱機関は, Carnotサイクルだけではない

ということである$${^{*3}}$$. 大事なのは, 最大効率が必ず $${100\% }$$ よりは小さくなるということである.

$${^{*3}}$$効率が最大になる熱機関のことをまとめてCarnotサイクルと呼ぶ教科書 (流儀) もある.

[1] 田崎晴明.『熱力学-現代的な視点から-』(2000, 培風館).
[2] 岸根順一郎.『物理学レクチャーコース熱力学』(2023, 裳華房).