
海外ポーカートーナメントのリスクマネジメント:バンクロールとの向き合い方
プロフィール
はじめまして。kimura634と申します。
✈️ フルタイムで働きながら年8〜10回海外ポーカー参戦中!
💼 仕事と両立しながら挑戦する実践的情報発信!
📅 スケジュール・🛫 航空券・🏨 宿・💰 バンクロール・🍽 食事・🚕 移動
🗺 トーナメント会場周辺情報も
⏳ 時間が限られてる方も「海外ポーカーを身近に感じたい!」方はフォローお願いします。
前置
サラリーマンの方や、サラリーマンではないけれど時間にそれなりに制約がある方視点での海外挑戦に役立つ情報を不定期で発信していきます。
今回はバンクロールとの長期的な向き合い方についての内容になります。
あくまでカジュアルに海外ポーカーを楽しみたい方向けのラフな記事です。無料ですのでお気軽にご覧ください。
「自分の許容リスクを知り、海外でのポーカー旅を長期的に楽しむためにシミュレーションを活用しよう!」
国内アミューズメントなどでポーカーを覚えて、海外で挑戦してみたいけれど、SNSなどを見ると海外プレイヤーはお金も時間もどちらもある人ばかりで、そもそもバンクロールもどれぐらい用意すればいいのかわからない。など不安要素が多く海外挑戦をあきらめている方も多いと思います。
今回は「トーナメントのバンクロールとの長期的な向き合い方」に焦点をあてて独断と偏見で解説していきます。
トーナメントとキャッシュゲームを比較すると、期待値通りに収束しやすいのはキャッシュゲームです。ポーカーを専業(生業)で行うならキャッシュゲームのほうが合理的な選択肢ですが、
「年に数回は海外で趣味としてポーカーを楽しみたい」
「キャッシュゲームよりトーナメントの方が好き。たまに行く海外だし自分が好きなトーナメントだけをプレイしたい」
「本業があるし、海外で使うお金は最悪無くなってもいい」
「結果として旅費分くらいの期待値は積めたらいい」
といったカジュアルな海外トーナメントプレイヤー向けに、長期的な期待値やリスクについて簡単にシミュレートする方法を紹介します。
シミュレーション方法
Tournament Variance Calculatorを活用
ポーカーのトーナメントには運の要素が大きく関わるため、最終的には失っても自分の人生に支障のないお金だとしても、長期的な結果を見据えてリスク管理をすることが重要です。
そこで、Tournament Variance Calculator
https://www.primedope.com/tournament-variance-calculator/
を使い長期的なリスクを計算する事ができます。
(以下※部分は補足内容が※備考下部に記載しています。)
モデルケース:Aさんの場合
年収:426万円(2024年平均年収)
家族構成:独身
年間休日:120日
海外ポーカーで失っても許容できる金額:年間平均100万円(10年間で1000万円)※1
年間の渡航回数:5回
年間エントリー数:30回(1遠征あたり6トーナメント)
遠征1回の経費:7万円(航空券・交通費・宿泊費・食費)※2
トーナメントのバイイン:1000$帯
想定ROI:20% ※3
100人規模のトーナメントを中心にエントリー
といったモデルケースの場合


of players 100 (参加人数)
Places paid 15 (インマネ人数)
Buy in 1000 (エントリー費用)
rake 15 (手数料%)
ROI 20 (投資利益率)
Number 300 (総エントリー数 6回×5遠征×10年)
Sample size 1000 (上記を1SETとして○○SET試行)
Bankroll 43333$ (650万円)
と各項目に入力して最後に
Calculator
を押してください。
各項目の見方
わかりにくい部分を抜粋した説明になります。
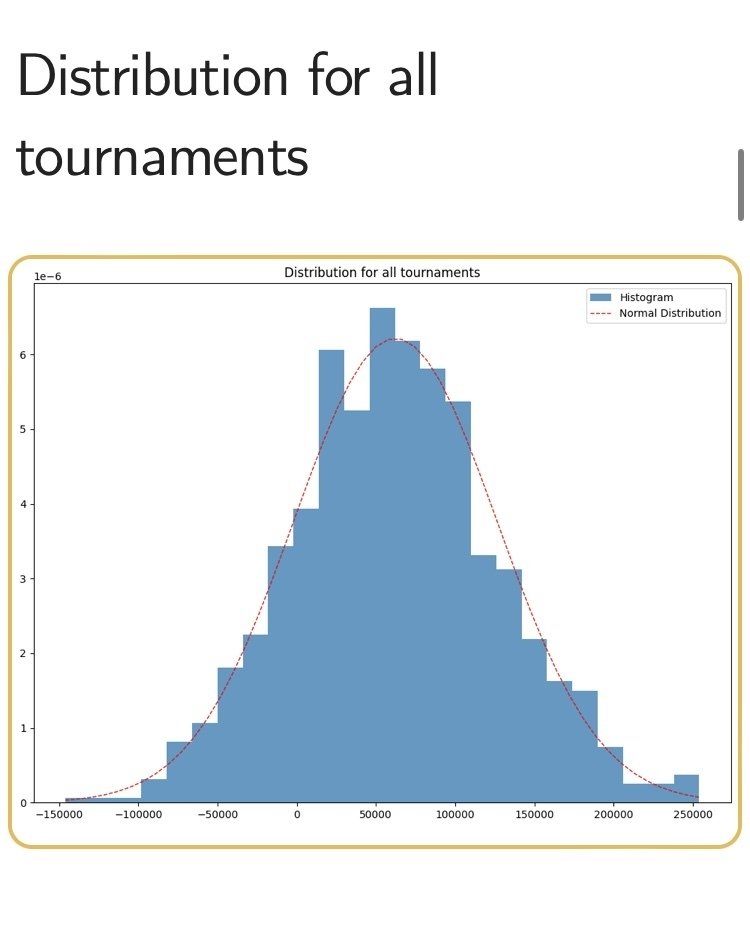
①Distribution for all tournaments
1000試行すべてのトーナメント収支の概ねの正規分布
ヒストグラム(青い棒グラフ)
→ 収支の頻度分布。
多くのプレイヤーの成績がこの範囲に収まることを示す。
赤い点線(Normal Distribution)
→ 正規分布(平均値を中心とした標準的な分布)。
実際のデータと比較し、収支の偏りや分散を確認できる。
X軸(横軸)
→ 収支
例えば「-150,000」は15万ドルの損失、「+250,000」は25万ドルの利益を示している。
Y軸(縦軸)
→ 収支の発生頻度(対数スケール)。
どの範囲の収支がどの程度の頻度で発生するかを示している。

②Random Samples
グラフの意味
X軸(横軸) → トーナメントの回数(0~300)
Y軸(縦軸) → 累積利益
黒線(Mean) → 平均的な成績(期待値通りに進んだ場合の結果)
緑線(Best run) → 最も好調だった試行
赤線(Worst run) → 最も不調だった試行
緑の帯(Confidence Intervals) → 信頼区間(70%、95%、99.7%)
→ 緑の濃い部分:結果が収まる可能性が高い範囲(70%)
→ 緑の薄い部分:より広い信頼区間(99.7%)

③Statistical Data
mathematically→数学的に計算した値
simulated→実際にシミュレーションした値
今回の記事で採用している値は全てsimulatedを採用
EVは期待値 ROIは投資利益率
SDは標準偏差の1σ(シグマ)平均値から約68.3%のデータが入る距離

④Confidence Intervals(simulated)
Random Samplesで表示された信頼区間1σ、2σ、3σの確率(≒70%、95%、99.7%)を数値として表したもの。
Confidence Intervalsは○○%で△△$~□□$の範囲でおさまるという解釈
ROI Intervals○○%で△△%~□□%の範囲でおさまるという解釈

⑤risk of run Bankroll needed
破産リスク(Risk of Ruin)と必要なバンクロール
破産リスク 必要なバンクロール
50% $16,768
15% $41,239
5% $63,979
1% $89,222
シミュレーション結果からわかる事※4
期待EV:62,250ドル(simulated)
破産確率:14%(バンクロールがすべてなくなる確率)※5
収支がマイナスになる確率:16%
1000回中一度も収支がマイナスにならなかった回数35回
70%の割合でEVが-3,486ドル~129,216ドルの範囲に収まる
最良のケースでは25万ドル以上の利益が出る可能性もある
最悪のケースでは11万ドル以上の損失もあり得る
上記をふまえるとEVの再現性は現実的な数字(70%頻度でROI-1.16%~+43.07%)かつ、破産確率(14%)とそこまで高くありません。(現実的な数字というのも個人の主観によるので完全に独断と偏見の意見です)
また終着点がプラスで終わる確率(84%)もそれなりに高く、確実にプラスで終わらないといけない!といったわけではないカジュアルにポーカーを楽しみたい層には精神的に許容できる結果ではないでしょうか?
モデルケース:Bさんの場合
では本業の収入、許容できるバンクロール、経費、期待値、挑戦する年数も全て同じケースでバイイン額を倍に上げて一撃狙いのリスクをとるBさんはどうなるか見ていきましょう。
Bさんは低確率とわかっていても
「最終的には5000万円以上を狙いたい」と考え、1000人規模のメインイベントを中心に、Aさんと同じく年間5回の遠征をします。
一度の遠征で複数DAYのトーナメントに参加するため平均で3エントリー行うとします。
メインや準メインなど、複数DAYの大規模トーナメントに参加し、
「最終的にマイナス収支で終わる可能性の方が多い事はもちろん覚悟している。10年以内に1000万円をそれなりの確率で全て失う事も構わない。」
といったスタンスで臨みます。
その場合以下のようなシミュレーションになります。
年収:426万円(2024年平均年収)
家族構成:独身
年間休日:120日
海外ポーカーで失っても許容できる金額:年間平均100万円(10年間で1000万円)
年間の渡航回数:5回前後
年間エントリー数:15回(1遠征あたり3トーナメント)
遠征1回の経費:7万円(航空券・交通費・宿泊費・食費)
トーナメントのバイイン:2000ドル前後
想定ROI:20%
1000人規模の複数day大規模トーナメントを中心にエントリー
といったモデルケースの場合


of players 1000 (参加人数)
Places paid 150 (インマネ人数)
Buy in 2000 (エントリー費用)
rake 15 (手数料)
ROI 20 (投資利益率)
Number 150 (総エントリー数 3回×5遠征×10年)
Sample size 1000 (上記を1SETとして○○SET試行)
Bankroll 43333$ (650万円)
と各項目に入力して最後に
Calculator
を押してください。





この場合期待されるシミュレーション結果からわかる事は
期待EV:55,390ドル(simulated)
破産確率:74%(バンクロールがすべてなくなる確率)
収支がマイナスになる確率:約52%
1000回中一度も収支がマイナスにならなかった回数10回
70%の割合でEVが-152,882ドルから+287,945ドルの範囲に収まる
最良のケースでは100万ドル以上の利益が出る可能性もある
最悪のケースでは22万ドル以上の損失もあり得る
とあたりまえですがどちらも同じバンクロールでmathematically的にも同じ期待EV額だとしても全く違うリスクを受け入れないといけなくなります。
この場合、勝てる時は大きく勝てる可能性がありますが、半分の確率でマイナス収支に終わるという点は注意が必要です。そもそも途中で破産する確率4回中3回です。
あたりまえのことですがEVのSimulatedとmathematicallyの乖離度合いもAさんに比べると激しくなります。
Simulatedとmathematicallyの乖離の程度感を確認したい場合は何度も同じ条件でCalculatorする事で違った1000Simulatedの値が出ますのでその方法で体感してください。
また、大規模トーナメントになるほど賞金の配分はTOP層に比重が重く、ITM時の下位層から中間層の恩恵は同じ上位%の結果でも小規模トーナメントよりはかなり少なくなり、結果小規模トーナメントと同じITM率や上位%を叩きだした場合でも収支のマイナスが長く続くことも珍しくありません。※6
仮に 最初の3年間で大きく負け越した場合、途中で精神的に撤退を余儀なくされるリスクもあるため、長期的に挑戦できるかどうかも考慮しましょう。
まとめ
同じトーナメントでも、参加人数の規模や試行回数などによって、期待しているEVと実際の結果との乖離は大きいのが一般的です。
全く同じ期待値を積んでいても、リスクの取り方次第でEVの再現性は大きく異なります。
海外トーナメントに求めるものは人それぞれ異なるため、どの選択が正解とは言えません。
リスクを抑えながら長く楽しみたいなら → Aさんのように小規模トーナメント中心に挑戦
ハイリスク・ハイリターンを狙うなら → Bさんのようにメインイベントを中心に挑戦
といった形で、自分のリスク許容度に合わせた選択、またはそれらをMIXするのが良いでしょう。
また自分がどれくらいのリスクをそもそも長期的に許容できるのかも事前に把握しておくことはとても重要です。
海外ポーカーの挑戦を検討する際、自分のリスク許容度を事前に知り、どれほどの不確実性を受け入れる必要があるのかを理解し腑におとすことで、より納得感のある挑戦ができるでしょう。
許容度は全ての人にとってとても個人差のあるものだと思いますので、
ぜひ、ご自身の条件に合わせてシミュレーションを試してみてください!
以上、最後まで読んでいただきありがとうございました。
今回の記事が参考になった方は、今後も海外ポーカーに関する有益な情報を発信する励みにしていきますので、ぜひXのフォロー・いいね・リポストをお願いします!
備考※
※1 毎年100万円までというわけではなく10年間で1000万円という設定です。今回の設定ではある程度スタート時点で貯蓄があるという前提でのシミュレーションになります。例えば1年目に1000$トーナメントを30回連続(15%のITM率でも0.7%程起こりうる事です)で滑れば-30000$で-450万円になります。今回のAさんの場合ですと基本的にはスタート時点で1/4の250万円程すでにバンクロールにある状態というのが精神衛生上望ましいかと思います。(破産確率50%が $16,768(約250万円))
バンクロールはエントリー費用の100倍、200倍とあるに越したことないのはもちろんですが、【生業】として活動するわけではないため、Aさんのような場合100万円でもいいからとりあえずチャレンジしてみてわ?と個人的には思います(主観)
※2 経費は1回の遠征で約7万円(航空券+宿泊費+交通費+食費)として想定。私が土日を挟んだアジア遠征する場合の実際の平均的な経費です。
よくあるパターンは木曜深夜の便で月曜日に帰国する3泊5日(ポーカーをプレイするのは金、土、日の丸3日間)
今回の場合7万円×5回×10年=350万円(23333$)が経費となります。
そのため今回のバンクロール設定は後述する43333ドル≒650万円=1000万円-350万円
※3 実際のROIはプレイヤーの実力やトーナメントのフィールドによって大きく異なります。初心者の場合はROIがマイナス(負け越し)になることも多く、逆に強いプレイヤーであれば今回設定した以上のROIを狙える可能性もあります。
真のROIを仮定する方法はこれまで有識者達が散々議論しているのでそちらを参考としてください。
あくまである程度の経験があり、適切なトーナメント選択ができるプレイヤーのケースとして、所謂勝ち組に該当し、かつ海外ライブトーナメントMTTの1000$帯で現実的なROIとして20%を採用しています。
つまり独断と偏見でそれなりに強いカジュアルプレイヤーが目指すべき現実的な数字として楽観的に20%と設定しているだけです。あくまで参考値なので最終的な値はご自身で設定してください。
※4 シミュレーション結果の破産確率以外に関してはバンクロールが無限という前提で試行した1000シミュレーションの結果です。
※5 ここでの『破産確率』は、ポーカー用に確保したバンクロールが尽きる確率(今回は$43333)を意味します。生活資金まで含めた財政破綻ではないため、あらかじめ失っても問題のない資金をバンクロールとして設定することが重要です。
※6 考え方の妥当性
一般的に、大規模トーナメントほど賞金分配がフラットになり、上位数%の賞金倍率が小さくなる 傾向があります。
•例: 1000人参加 → 30位はエントリーの3.5倍
• 例: 100人参加 → 3位はエントリーの10倍
逆に、小規模トーナメントは賞金分配がトップヘビーになりやすく、上位の賞金倍率が大きくなる ことが多い。
バブル付近の賞金差
大規模トーナメント では、バブル付近(最低インマネ額)はバイインの約1.5倍程度になることが多い。
小規模トーナメント では、入賞人数が少なく、バブル付近の賞金がエントリーの2~3倍になることもある。
これも「上位%の賞金額が違う」理由の一つ。
賞金配分はトーナメントごとに異なるので 過去の実績(Hendon Mobなど)を確認してください。
特に 保証賞金の有無やバブル付近の賞金分布 も考慮すると、より正確な比較ができるかと思います。
