
読書ノート:生成AIの仕組み - <流れ>が画像・音声・動画をつくる、岡野原大輔
はじめに
日頃、大規模言語モデル(LLM)については追っているが、Stable Difusionなどの、いわゆる拡散モデル系の生成モデルは不勉強であった。確率過程のように、ノイズから信号が生成されるような生成過程のモデルという理解であったが、あってるのだろうか?ARCベンチマークのような、新しい入力に対しても柔軟に対応できるような汎化能力ってのも、拡散モデル系だとどうなるんだろうという疑問もある。
図:“Flow Matching on General Geometries”, R. T. Q Chen and Y. Lipman, ICLR 2024
追記:岡野原さんの、「拡散モデル」本のノートを別途追加した。
フローマッチングの元論文の紹介はこちらのyoutubeがよい。
感想
数式をつかわないと謳われているので、一気読みしてみたが、消化不良。
画像生成などで「拡散モデル」とか、最適輸送とか、物理学(ボルツマン分布、ヘルムホルツエネルギー等)とか最適化(最適輸送問題)と生成モデルが強く関連するという分野があるという話は以前から聞いていたが。確かにこの本は数式を使わず、分りやすく説明してくれた。エネルギーベースモデルでボルツマン分布がでくるところとか、流れをつかったモデルは最尤推定にもとづき分散統治型であるとか、スコアベースモデルと拡散モデルの同一性とか見所はたくさんあった気がする。拡散モデルのところで、デノイジングスコアマッチングがシミュレーション・フリーで生成モデルを求めることができるとか、最適輸送を基本の流れとして複数の流れを束ねるのがフローマッチングとかの発展まで俯瞰できた。
ただ、拡散モデルが、確率微分方程式(SDE)で定式化できるから、そちら方面の知見が生かされて、、、みたいな話は出てこなかった気もする。
とにかく、あまりにも大量の情報が式なしで語るのは、あの最先端のarxiv論文を数行でまとめる岡野原さんの言語能力の高さの証明でもあると感じた。岡野原さんの解説が読める日本人は幸せである。
最後に、o1-preveiwとClaude 3.5 Sonnetに読書ノートに基づく質問とか概念図を作ってもらったり、時系列モデルとの類似性を整理してもらったが、やっぱり消化不良。
また数日して読書メモを見直しながら精進したいところである。
追記:o1-previewに読書ノートをファンタジー風、正法眼蔵風でまとめてもらった
広大で奇妙な高次元の世界において、データたちは低次元の秘められた多様体という名の秘境に潜んでいた。その多様体を見つけ出し、データの真の姿を映し出すために、賢者たちは「流れ」と呼ばれる魔法を紡ぎ出す。エネルギーという見えざる力を操り、彼らは単純な分布から複雑な模様を描き出し、高次元の迷宮を自在に渡り歩く。かつてはエネルギーベースの古の術式がその道を阻んでいたが、流れの魔法がもたらす新たな煌きによって、その制約は打ち破られた。こうして、データの生成という錬金術は、流れの力によって未知なる創造の扉を開き、多様体の秘密を解き明かしていくのであった
高次元の広大なる境界において、データの真相は多様体という隠れた道に伏す。流れを悟る者は、単純なる事前分布より複雑なる分布を生み出し、高次元の迷宮を自在に巡る術を得る。エネルギーの理を識り、その流れを用いて、分配関数の障壁を越え、局所的な変容により確率分布を自在に操る。かつてはエネルギーベースの古き法により道は阻まれしが、流れの法門を開くことにより、その妨げは消ゆ。斯くして、流れを用いた生成の妙法により、多様体の秘めたる構造を顕現し、データ生成の真理を悟るに至る。
読書メモ
主に気になった個所をマーカーで線を引き、これをピックアップした。なお、kindleで読んでいるのでページ数(..PXX)はあてにならない
生成AIの仕組み - <流れ>が画像・音声・動画をつくる
広大で奇妙な高次元空間:
高次元空間は単に広いだけでなく、内側から外側に向かうにしたがって圧倒的に広くなっていく奇妙な空間である..P30
生成において正解の出力は1だけではない:
生成タスクでは、1つの値をわりあてられるように学習していくのではなく、無数の正解を割り当てられるように学習する必要がある..19%
多様体仮説ーデータは低次元に埋め込まれている:
1つめは多様体仮説である。世の中のデータは見かけ上の次元数よりもずっと少ない数のパラメータで表現できる空間に分布していると考えられている。この仮説を多様体仮説と呼ぶ。..19%
多様体上の近さともとのデータ空間の近さは一致しない..21%
多様体上では元の情報を非常に圧縮した形で表現できている。
このような多様体という新たに分布するデータを考え、多様体とデータ空間とを相互変換する仕組みがあれば、生成ができるようになる。..P33
生成モデルの大きな目的の一つは、この多様体の構造と、多様体とデータ空間の間を変換する方法を学習することだといえる。つまり生成モデルとしては、高次元を多様体空間中でデータを構成する多様体がどのように分布しているかをみつけ、その多様体から新しいデータを生成できるようになることが重要である。..P34
対称性ーデータは変換に対する不変性がある:
構成性ーデータは多くの部品の組合せで成り立っている:
2.生成AIの歴史
イジングモデルからホップフィールドネットワークへ:
ホップフィールドネットワークではこれら(粒子間の相互作用や粒子ごとに好まれる状態)がパラメータとして学習によって決まる
この更新は、ヘブ則とよばれる更新則に従ってニューロン間の重みを書き換えていくことで達成される。..P44
エネルギーが低くなるようにニューロンの状態を更新していくことで、学習時にみたようなデータを生成できる。
必ずしも学習データと全く同じデータではなく、異なる新しいデータを生成するようにもなる。パラメータを更新する際に、他の様々な異なる状態のエネルギーも同時に低くなっていたためである。機械学習における汎化と同じことが起きている。..P46
エネルギーベースモデルとは:
物理世界において、系(考察の対象)のエネルギー(内部エネルギーと呼ばれる)は自由エネルギーとその他に分けることができる。熱力学第二法則により、系の自由エネルギーは減少する方向に自発的に変化する。本書では単にエネルギーという場合、自由エネルギーを指すものとする。..P47
エネルギーの仕組みを用いた生成モデルは次のように実現される。
ニューラルネットワークを使ってエネルギー関数を表しており、
ある情報を記憶、その位置のエネルギーが低くなるようにエネルギー関数を更新する…P49
エネルギー関数はパラメータで表されると説明した。この場合、ある位置エネルギーを低くするようにパラメータを更新すると、無数の他の位置のエネルギーの値も変わり、エネルギーが低くなったり、高くなったりし、これにより学習時にみたことがないようなデータが生成される、汎化が起こることを期待する。
どの犬の画像を思い出すかは、どこからスタートしたかという初期値によって変わる。..P49
エネルギーベースモデルは連想記憶を自然に実現する
エネルギーベースモデルの大きな特徴は、ある刺激をもとに他の記憶を思い出すという連想記憶を自然に達成できることである。..P49
そして、エネルギーが低くなる画像の状態を求めることで、テキストに対応する画像を生成できる。
エネルギーベースモデルはこのように連想記憶を自然に実現できる。固定した側を生成の条件と考えると、条件付き生成を実現していることになる..P52
エネルギーと確率の対応:ボルツマン分布
物理世界においてエネルギーと確率はボルツマン分布によって相互に変換できる。
ボルツマン分布ではエネルギーが低ければ低いほど、確率は大きくなり、逆にエネルギーが高いほど確率は小さくなる。
温度が高くなると確率分布は一様に近づき、逆に温度が低くなるとエネルギーが一番低い状態のみが確立1をもつような確率分布となる。..P53
ランジュバン・モンテカルロ法
(ボールは必ずしも低い位置にとどまるわけではなく)外からのランダムな力によって常に揺れ続ける
ボールを転がし続け十分時間がたった後にボールがどの位置にあるかという確率は、ボルツマン分布に従う。このようにしてデータをボルツマン分布に従ってサンプリングすることを、ランジュバン・モンテカルロ法と呼ぶ。
各状態/データにエネルギーが割り当てられているとき、ボルツマン分布を用いて、そのエネルギーを確率分布に変換することができる、逆に確率分布をエネルギーに変換することもできる。..P56
エネルギーベースモデルの致命的な問題
サンプリング、生成がとても遅い
学習もとても遅い
これらの問題により、エネルギーベースモデルは理論的には美しいが、大規模な学習問題にはそのままでは適用が難しいとされている。..P58
空間全体の情報を支配する分配関数
ボルツマン分布に基づく確率分布を求める場合も、すべての状態の非正規化確率の合計を求め、非正規化確率を合計値で割る必要がある。この合計値を分配関数(または状態和)と呼ぶ。..P60
高次元空間では、すべての状態の非正規化確率を列挙してその合計値を求めることは、状態の種類数が膨大であることから基本的に不可能である。
(このことが)高次元データ上の確率分布を設計するのが難しい問題の本質である..P61
データは隠れた情報から生成されている
潜在変数とは対象データ全体の意味を表すとともに、それを要約した情報である。
潜在変数上でデータを少しづつ変化させると、観測変数も変化していくと考える。
生成するためには認識が必要
潜在変数モデルによる生成モデル、ヘルムホルツマシン(ダヤン、ヒントン)
ヘルムホルツエネルギーとは、熱力学に由来する自由エネルギーのこと。
ヘルムホルツマシンは、データから、それを生成したであろう潜在変数を推定する認識モデルと潜在変数からデータを生成する生成モデルを交互に学習するという考えを導入した。..P64
変分自己符号化器(VAE)
潜在変数モデルを進化させ、高次元の画像データを生成可能にしたのが変分自己符号化器である。
VAEでは変分ベイズとよばれる方法を使って学習目標を定め、認識モデルと生成モデルの更新を同時に行う。..P67
VAEにおいては、潜在変数の次元を小さくするだけではなくて、ノイズを加えた上で復元するという問題を学習時に同時に解く。さらに潜在変数の分布は正規分布に近づくような制約を加えて学習する。
生成する際に、認識モデルは使わず、潜在変数を正規分布からサンプリングし(潜在変数の分布は正規分布に近づくように学習している)、次に生成モデルが潜在変数からデータを生成する。
VAEによって、獲得された製剤変数空間は、多様体仮説で提唱されたようなデータ分布の隠れた低次元空間をとらえることに成功していることが分かった。..P69
潜在変数モデルの問題
認識モデルの学習が難しい
コラム:自己回帰モデル
分配関数の計算が問題→問題を分配関数の計算が可能な小さな問題に分割し、それぞれの問題を解く
その代表的な手法が自己回帰モデルである。
現在の大規模言語モデルは自己回帰モデルをつかっている、近似ではなく、正しい確率分布を推定でき効率的に高次元データを扱えるが、分解の仕方に引きつられる、生成が遅くなる。
3.流れを使った生成
流れとは
生成モデルを扱う上で重要な性質は「連続性」である。原因なく消えたり現れたりしないこと、ワープなどもしない。
連続の式
ある位置の物質の変化量と、その位置からの周囲への流出量または流入量は常に釣り合っているという関係を表した数式を、連続の式、または連続の方程式とよぶ。
流れをつかって複雑な確率分布を作り出す
流れによって分布を変えたとしても、全体の量はかわらない。
この性質は、流れを使って確率分布を扱う上で重要な性質となる
高次元空間においては分配関数を求めることは、不可能なくらい難しい。
流れを使うことによって、分配関数を求めずに、なおかつ複雑な確率分布を設計できる。..P83
図24:簡単な確率分布を流れを使って変えてゆき、任意の複雑な確率分布をつくることができる。連続の式で保障されたように、どれだけ複雑な流れをつかったとしても確率分布であることが保証される。
事前分布をわりあてる、事前分布は一様分布であったり正規分布がよくつかわれる。
次に、この状態に割り当てられる確率を、各位置の密度のようにあつかう、そして、この事前分布からスタートした上で各位置で流れを起こし、分布を変えていくことを考える。
この流れは位置ごとにその位置にある物質がどのような速度で周囲に流出あるいは流入するかを表す。流れは時刻ごとにかわってゆくとする。
変化していって最終的に得られた分布をモデル分布と呼ぶことにする。事前分布とは全く違う複雑な分布になることもできる。
流れを制御することによって、どのような分布を作るのかを制御することができる。
流れをつかったモデルは分配関数を求める必要がない
図25、各状態に確率を割り当てる問題を寄付の例といて考える。エネルギーベースモデルはあたかも全員の寄付額の情報をもとに合計値が目標に達成するように調整する中央集権型。流れを使った生成は、全員で一定額負担するようにしたあとで、個別に負担額を周囲と調整してよいとする分散倒置型。
流れを使ったアプローチでは局所的な流れを操作する分散統治型のモデルであるといえる。
流れを使う場合は、局所的な情報である流れを操作して確率分布を操作でき、全体を把握しなくても分布全体が確率分布として成り立つことが保証される。
正規化フロー・連続正規化フロー
流れを使うことで、分配関数を計算することなく複雑な確率分布をあらわすことができる。
ディンらが、正規化フローを提唱、事前分布を可逆な変換で徐々に変換し、複雑な分布を構成する手法。
さらに、チェンらが正規化フローを発展させて連続正規化フローを提案。
正規化フローでは可逆変換を使わなければいけなかったが、連続正規化フローでは流れを直接モデル化しており、そのような制約はない。
流れを使ったモデルは、連続正規化フローで完成された。
連続正規化フローでは各位置、各時刻における流れをニューラルネットワークによってモデル化する。
流れをつかって尤度を求め、それを最大化するように学習する
正規化フローや連続正規化フローの学習は、最尤推定によって行われる。
流れをつかった生成では、(あるデータに割り当てられた確率)尤度を求めることができる。
体積の変化に基づいて密度がどれだけ変わるのかがわかる。
モデル分布におけるあるデータ、つまり高次元空間のある点に割り当てられた確率を求める場合を考える。その点にたどり着く流れを逆向きにたどっていき、各瞬間の流れにおいて、その程度その点が圧縮されたり、膨張されたかを求めればよい。そして最終的に事前確率にたどり着いたときに、事前確率の際に割り当てられている確率と、流れの中でどの程度膨張したのか、圧縮したのかという情報をもちいれば、モデル分布の確立を求めることができる。
図26:流れを使った生成では、モデル分布の各点で割り当てられている確率を求められる。その際は、モデル分布とその点に到達する流れを求め、事前確率で割り当てられていた確率と流れの過程での確率の圧縮/膨張割合を求める。
このようにして、与えられたデータの尤度(モデルが割り当てた確率)を求められる。そして、尤度を最大化するように流れを調整する。流れはニューラルネットワークによるモデルで調整されているので、ニューラルネットワークのパラメータを調整し、尤度を大きくするように更新できる。こうすることで、学習データを高い確率で最終的に生み出すような流れを作ることができる。
流れに沿ってデータを生成する
事前分布上の位置からモデル分布上での位置にむけて流れにそって徐々に変換する、長いステップ数は不要。
つまり、事前分布からサンプリングされた時点で、最終的にどの位置に到達するかが決まっている。
流れは複雑な生成問題を簡単な部分生成問題に分解する
流れによるデータ生成というのは、事前分布から得られた何も秩序をもたないデータを最初の潜在変数とし、次の潜在変数を生成すrという生成過程の積み重ねにより、最終的なデータを得ることに相当する。
流れによる生成によって複雑な生成問題を、部分生成問題に分割しているのだ。
なお、流れによる生成を学習して獲得される生成過程は、実際のデータを生成する過程とは異なる。
流れをモデル化する
ベクトル場はニューラルネットワークを用いて効率的に表すことがdけいる。入力として空間座標を受け取り、その位置における流れを表す速度ベクトルを出力する。
速度ベクトル場という膨大な情報を、ニューラルネットワークのパラメータとして非常に高い圧縮率で保存しているといえる。
流れの結果の計算
あるデータが流れに沿って移動していく様子をシミュレーションする場合には、時間を区切った上でそれらの区切られた間に発生した変位置をけいさんし、それらの変位置を足してゆく必要がある。
流れを使った計算は、生成過程を細かいステップに分解しているということができる。
正規化フローの課題
正規化フローではモデルに使用できる変換に大きな制約がある。入出力が一対一対応する可逆変換であること、圧縮や膨張の割合を効率的に求められるものでなければならない。
学習時に非常に大きなメモリが必要
不要に難しい流れを獲得しまう場合が多い。
学習中に流れ全体をシミュレーションする必要があるので、大きなモデルが使えなかった。
4.拡散モデルとフローマッチング
拡散モデルの発見
拡散モデルは、2015年、ソーディックスタインらによって、非平衡熱力学に基づいて提案された
2019年、ソングらが、スコアと呼ばれる確率分布に基づく流れを推定し、それをつかった高品質なデータが生成できた。これをスコアベースモデルとよぶ。
学習データから遠くはなれた位置にはスコアによる流れが発生せず。データ生成が失敗。そこで学習データに徐々に強いノイズを加えて崩していき、学習が行われる領域を空間全体に広げた上で、それぞれの崩した確率分布におけるスコアを求め、それらを組み合わせて使うことで高品質な生成に成功できることを示した。
2020年に、ホーらが、スコアベースモデルと拡散モデルが、実は同じ問題を解いていることを示すとともに、モデルや学習の工夫によって、それまで提案されていた生成モデルに匹敵する高品質な生成ができることを示した。
これと並行して、言語モデルなどのテキストデータの生成モデルも大きな成功を収めていた。
2021年ごろになると、DALL-EやCLIPなど、言語モデルによって作られたテキストによる条件付けと画像生成を組み合わせることで、言語で支持を出して画像を生成できるという手法が多く登場した
一般の拡散現象
秩序をもった対象にノイズが加えられて徐々に破壊されて完全な無秩序になる過程を逆向きにたどることで、無秩序から秩序を生み出す過程、すなわち生成を実現できるのではないか?という考え方が、拡散モデルの基礎となるアイデアである。
拡散モデルとは
学習データは空間中に秩序をもって分布している、これをデータ分布と呼ぶ
次に、これらのデータにノイズを加えていき破壊してゆく。一般に計算にしやすさなどから、正規分布に従うノイズを加える場合が青おい。ブラウン運動ににている。
ノイズが一定の条件を満たすならば、ノイズの合計の分布は正規分布。ノイズは一般に強度を上げながら加え続け、データが正規分布からのサンプルと区別がつかなくなるまで続ける。
生成はこの逆をたどる。
つまり拡散過程は、確率分布をデータ分布から正規分まで変化させてゆく、逆に生成過程は正規分布からデータ分布へと変化させる。
これが拡散モデルによる生成モデルのが学習となる
拡散過程が生み出す流れ=スコア
確率が大きい位置から小さい位置に向かって広がっていく流れが生じている
この流れと逆向きの流れをスコアと呼ぶ。
拡散過程を逆向きにたどるためには、各時刻・各位置で発生していたスコアに従って変化させていけばよい
スコアとエネルギーの関係
各地点で確率の自然対数をとった値が最も急激に大きくなる方向とその変化の大きさを表したベクトルをスコアとよぶ。
拡散モデルに基づいてデータを生成する流れというのは、エネルギーが最も急激に小さくなる流れと一致する。言い換えればエネルギーベースモデルでエネルギーを小さくしていくという流れとスコアは一致する。
(エネルギーベースモデルの場合はエネルギーは時刻と共に変わらないが)拡散モデルの場合は時刻とともにエネルギーが変わるようになっている。この違いは重要で、拡散モデルが多様性のあるような分布からでも効率よくデータをサンプリングできる理由となっている。
時間ともにスコアは変化していく
図34:スコア(矢印)は確率が高い領域がどこかを表す流れとなっている。また時刻ごとに流れは変わり、事前分布に近い頃では遠くのほうから徐々に寄せていく流れとなっており、データ分布に近づいていくとデータ分布の詳細な違いを捉えるような流れとなる。
デノイジングスコアマッチング
(スコアを求めれば、拡散モデルはデータを生成できるが)このスコアは、データ分析から事前分布へと向かう流れの全体をシミュレーションしなくても求めることができる。これが拡散モデルの大きな特徴である。
(学習のために毎回シミュレーションしようとすると)計算量が大きくなりすぎるという問題があったが、デノイジングスコアマッチングはこれを解消した。
まず、学習データからデータを1つサンプリングする、次にデータ分布から事前分布へと変換させていく間の途中の時刻を1つサンプリングする。そして、時刻に応じたノイズの強度を求め、その強度でデータにノイズを加える。
ニューラルネットワークは、ノイズが加わったデータと時刻から、ノイズが加わる前のデータを予測できるように学習する。
直感的には、デノイジングは現在のデータ分布にノイズを加えた上で、元に位置に戻る方向を推定することになる。このとき、元に位置に戻る1つ1つの方向はバラバラだが、全体として確率分布の方向に垂線を下した方向が得られる。これは確率の対数をとった分布を等高線としてみたときに、その等高線の傾斜を推定しているのと同じである。
シミュレーション・フリーな学習は学習の一部分を切り出す
デノイジングスコアマッチングは流れ全体をシミュレーションせずに学習できるという利点があった。
シミュレーション・フリーであれいば、流れを学習する際に、流れの一部分だけを取り出してそこを修正することを繰り返せば学習することができる。
シミュレーション・フリーである手法によってはじめて、今日のような大きなモデルでかつ大量の学習データをつかって安定的に学習できるようになった。
拡散モデルによって生み出される流れの特徴
拡散モデルはガウシアンノイズが規定した流れによって、概要から詳細を順に生成する流れをつかって生成するのだ。
このように、拡散モデルによって得られる生成過程は、データの生成過程と似た流れをもつ。このため学習がしやすく、汎化もしやすいと期待される。
拡散モデルと潜在変数モデルの関係
データ生成の系統樹を自動的に学習する
ノイズによってデータがの区別がつかなくなっていく過程は、データの系統樹をつくっているようにみなすことができる。
データの生成はまさにこの逆向きに、どのようなデータを生成するのかの分岐点の選択をしているようにみなすことができる。
拡散モデルはエネルギーベースモデルである
拡散モデルはエネルギー関数を直接推定する代わりに、そのエネルギー関数の各地点での傾きであるスコアを推定している手法とみなすことができる。
拡散モデルは流れを使った生成モデルである
(正規化フロー、連続正規化フローとは違って)デノイジングスコアマッチングにより、シミュレーション・フリーで学習できるとともに、拡散過程で決まるスコアという性質の良い流れをつかって学習している点が大きな違い。
拡散モデルは、様々な生成モデルによる生成方法の集大成になっている。
フローマッチング:流れを束ねて複雑な流れを作る
フローマッチングは基本単位の流れを複数束ねることによって、複雑な分布間の流れを求める。
フローマッチングが特に協力なのは、とりわけ性質の良い最適輸送とよばれる流れを基本単位の流れとして使った場合である。
最適輸送とは
最適輸送は、確率論や最適化理論などで広く使われている数学的概念である。
全体のコストが最小となるような移動先への移動を最適輸送と呼ぶ。
最適輸送をつかった生成
事前分布からデータ分布への最適輸送を求めることがえきれば、事前分布からサンプリングし、それを最適輸送で変換した結果はデータ分布からのサンプリングとすることができる。
最適輸送によるながれは、1ステップで生成することができる。
拡散モデルをつかったサンプリングは数百から数千ステップを必要としていたので、数百倍から数千倍の高速化が達成できる。
最適輸送を直接求めるのは計算量が大きすぎる
こうした問題を回避するために、フローマッチングにもとづく手法は、計算可能な大きさの最適輸送の問題に分解し、それらの流れを重ねることで分布間の流れを求める。
フローマッチングによる学習
図38:フローマッチングにもとづく事前分布からデータ分布への流れの学習。データ分布からサンプリングされたデータ点を分布とみなし、事前分布とデータ点をぼかかした分布間の最適輸送を予測できるように学習する。これらを束ねた流れは、事前分布からデータ分布への流れとなる。
フローマッチングはデノイジングスコアマッチングと同様に、シミュレーションを必要としない。局所的な流れを推定できるようにモデルを学習していくことによって、全体の流れを再現する。
フローマッチングの発展
条件付き生成は条件付き流れで実現
潜在拡散モデルー元データを潜在空間に変換して品質を改善
5.流れを使った技術の今後
汎化をめぐる謎の解明
生成というタスクにおいては2つの意味で汎化を実現する必要がある。1つ目は、生成対象の汎化。2つ目は条件の汎化である。学習の際には1部の条件しか与えられれない、生成後に初めて与えられる条件に対しても正しく対応できるように汎化する必要がある。
ニューラルネットワークはもともと、様々なタスクにおける汎化能力が優れていることが示されている。
拡散モデルの定式化による汎化が非常に強力であることが理論解析や実験結果から示されている。
注意機構と流れ
注意機構はいくつかの制約のもとで、エネルギーベースモデルとして表現することが可能である。
逆に、注意機構による状態の更新は、エネルギーのような量を減らしていく操作に対応するとみなせせる。
注意機構によって生じるデータの流れは、エネルギーベースモデルにおける状態更新の一種と解釈できる。
流れによる数値最適化
最適化問題を流れをつかった生成を用いて効率的に解決できる可能性がある。
目的関数を最小化するような入力を求める問題
この場合、目的関数の値をエネルギーとみなし、ボルツマン分布を通じて、拡散モデルによる生成問題とみなすことができる。
このように考えると、目的関数を最小化する入力は、生成確率がもっとも高いサンプルに対応する。
言語のような離散でーたの生成
流れを使った生成は、大規模言語モデルにおいては、現時点で十分な成果をあげていない
主な理由は、言語が離散的なデータであるためとみられている
各種生成AIによる読書ノートまとめ
Claude 3.5 Sonnet
流れによる生成モデルは、データ生成を連続的な変換過程として捉え、単純な事前分布(正規分布など)から複雑なデータ分布への変換を実現する革新的な手法である。この手法の核心は、分配関数計算の困難さという生成モデルの本質的な課題を回避しつつ、局所的な流れの制御によって大域的な確率分布を操作できる点にある。特に拡散モデルは、データにノイズを加えて徐々に秩序を破壊していく過程を逆向きにたどることで生成を実現し、デノイジングスコアマッチングによって流れ全体のシミュレーションなしで効率的な学習を可能にした。また、概要から詳細へと順に生成する特徴を持ち、これは実際のデータ生成過程に似た性質を持つため、学習と汎化が容易になる利点がある。さらに、拡散モデルはエネルギーベースモデル、潜在変数モデル、流れを使った生成モデルの特徴を併せ持ち、様々な生成モデルのアプローチを統合した集大成として位置づけられる。近年では、フローマッチングという手法により、最適輸送の考え方を用いて生成の高速化も実現されている。
o1-preview-2024-09-20
流れを利用した生成モデルは、単純な事前分布から始めて、ニューラルネットワークでモデル化された流れ(フロー)を通じて複雑な確率分布を構築し、高次元データの生成を実現する手法です。エネルギーベースモデルのように全体の分配関数を計算する必要がなく、局所的な流れの操作によって確率分布を変換できるため、効率的な学習と高速な生成が可能です。正規化フローや連続正規化フローでは、可逆変換や速度ベクトル場を用いてデータ空間と多様体との相互変換を学習し、多様体仮説に基づくデータの隠れた低次元構造を捕捉します。これにより、従来の生成モデルが抱えていた学習やサンプリングの遅さ、大規模なメモリ消費といった問題を解消し、エネルギーベースモデルや潜在変数モデルの課題を克服して高品質なデータ生成を可能にしています。
Gemini 2.0 Flash Exp
流れによる生成モデルは、複雑なデータ分布を、連続的な変換を用いてシンプルな事前分布から生成するアプローチです。このモデルの中心となる考え方は、データ分布を確率密度として捉え、その確率密度を時間とともに徐々に変形させる「流れ」を定義することです。具体的には、事前に設定された簡単な分布(例えば、ガウス分布や一様分布)を「事前分布」として設定し、この分布から出発します。次に、各位置において物質がどのように移動するかを表す「流れ」を、ニューラルネットワークを用いてモデル化します。この流れは、各位置における物質の流出や流入の速度を表すベクトル場として表現され、時間とともに変化します。流れに沿って事前分布を変形させることで、徐々に複雑なデータ分布を生成していくことができます。この過程で重要なのは、流れによって分布の総量は変化しないという連続性の原理です。この性質により、どれだけ複雑な流れを使っても、最終的に生成される分布が確率分布として成立することが保証されます。流れモデルの大きな利点は、従来の生成モデルで課題となっていた分配関数の計算を回避できることです。分配関数の計算は高次元空間では非常に困難ですが、流れモデルでは局所的な情報である流れを操作する分散統治的なアプローチを採用することで、全体の分布を把握せずに分布を生成できます。さらに、流れモデルは可逆な変換を用いることで、モデル分布の各点における確率を計算することも可能になります。このため、最尤推定に基づく学習が可能となり、学習データに対して高い確率を割り当てるような流れを学習できます。
o1-preview-2024-09-20とのQ&A
読書メモから主要トピックとそれらの間の関係性をまとめてもらったり、時系列データの取り扱いとの類似性について整理してもらった。
主要なトピック間の関係性まとめ
高次元空間の問題を解決するために、多様体仮説や潜在変数モデル(VAEなど)が提案された。
エネルギーベースモデルは、エネルギーと確率の関係を利用して生成を試みるが、計算コストの問題がある。
流れを使った生成モデル(正規化フローなど)は、エネルギーベースモデルの課題を克服しつつ複雑な分布をモデル化する方法として登場。
拡散モデルとスコアマッチングは、ノイズを利用して効率的な学習と生成を実現し、現在の生成モデルの主流となっている。
フローマッチングや最適輸送の概念は、さらに高速で効率的な生成を可能にし、生成モデルの可能性を広げている。
将来的には、これらの技術を組み合わせて汎化性能の向上や離散データの生成など、より高度なタスクへの応用が期待される。
時系列データ・確率過程との類似性について
この、流れによる生成モデルの話と、時系列データにおける確率過程の話題との類似性を整理してほしい、ブラウン運動や、ノイズからAR過程をなどを経て時系列データが生成される様子など。
流れによる生成モデルと時系列データの確率過程には、多くの共通点があります。
・確率的なダイナミクス: 両者とも確率的な動的システムを扱い、ノイズや確率微分方程式を用いてデータの変化をモデル化します。
・ノイズの役割: ノイズはデータの生成や変動の主要な要因であり、初期状態からデータを生成する鍵となります。
・連続的な変換: データは連続的または漸化的な変換を通じて進化し、確率分布も時間とともに変化します。
これらの類似性は、流れによる生成モデルの理解を深め、時系列データのモデリングにおける確率過程の知識を応用することに繋がります。また、逆に時系列データの生成や予測において、拡散モデルやフローマッチングなどの手法を応用する可能性も示唆しています。
Claude 3.5 Sonnetによる概念マップ
Claude 3.5 Sonnetに読書メモから概念マップを作ってもらった。以下はその一部、右に切れているのは、その2「流れを使った生成」につながっている。
生成モデルの基礎概念

流れを使った生成

時系列・確率過程との類似性
この類似性の理解は、両分野の手法の相互応用に役立つ可能性があります。例えば:
・時系列モデルの推定手法を生成モデルの学習に応用
・生成モデルの効率的なサンプリング手法を時系列予測に活用
・両者の理論的な解析手法の共有
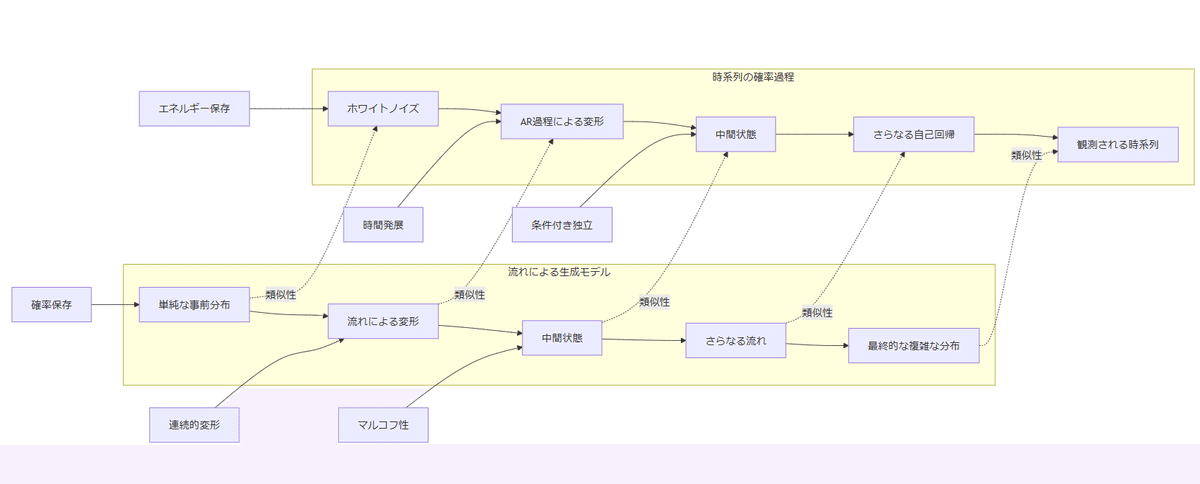
さすがClaude 3.5 Sonnet、類似性を見つけて、これをちゃんとmermaid形式の図としてもわかりやすく表現できるのは、脱帽ものだ。
