
一発裏無しが面白い。安めを見逃せる境界巡目のセオリー!?
こんにちは。髙倉 拓馬(メタビート)です。いつも記事を読んで下さってありがとうございます!
この記事は無料で全文読むことができます!記事が良いと思って下さった方はご購入とスキ、Twitterでのシェアをぜひお願いします!
私、髙倉拓馬(メタビート)、久しぶりにタイトル戦の予選で勝ちました。
31114で通過!
— 高倉 拓馬/メタビート (@metabeatdown) February 4, 2024
ダマメンホンチートイドラドラあがったり早いピンフ手をあがり続けたりやりたい放題でした
最後の半荘も2万点ラスで通過なのに無限にリーチに押せる手がくるから大変でした
久しぶりの予選通過で嬉しい!全国大会も頑張ります https://t.co/S1P11Tttmv
それがこの「BIG1カップ」といわれる麻将連合さん主催のタイトル戦。
一発裏無し、テンパイ連荘、テンパイ料がありのルールで、日本プロ麻雀連盟さんの公式ルールと似ています。
最近このルールをセットやら追っかけやらでやることが多いのですが、その中でかなり面白い局面に出会いました。出現頻度も結構あると思うのでご紹介します!
期待値計算:リーチ後にアガリ牌を切ることなんてある!?

親番の手牌。ど高めはタンピン三色の手牌。跳満も見える超勝負手です。
1sは超安めで、正直アガリたくはないですよね。
…では、見逃してはどうか?ツモっても切ってしまえばいいのではないか?という仮説を考えました。
とりあえず、例の麻雀何切るシミュレーター君に解析させてみました。
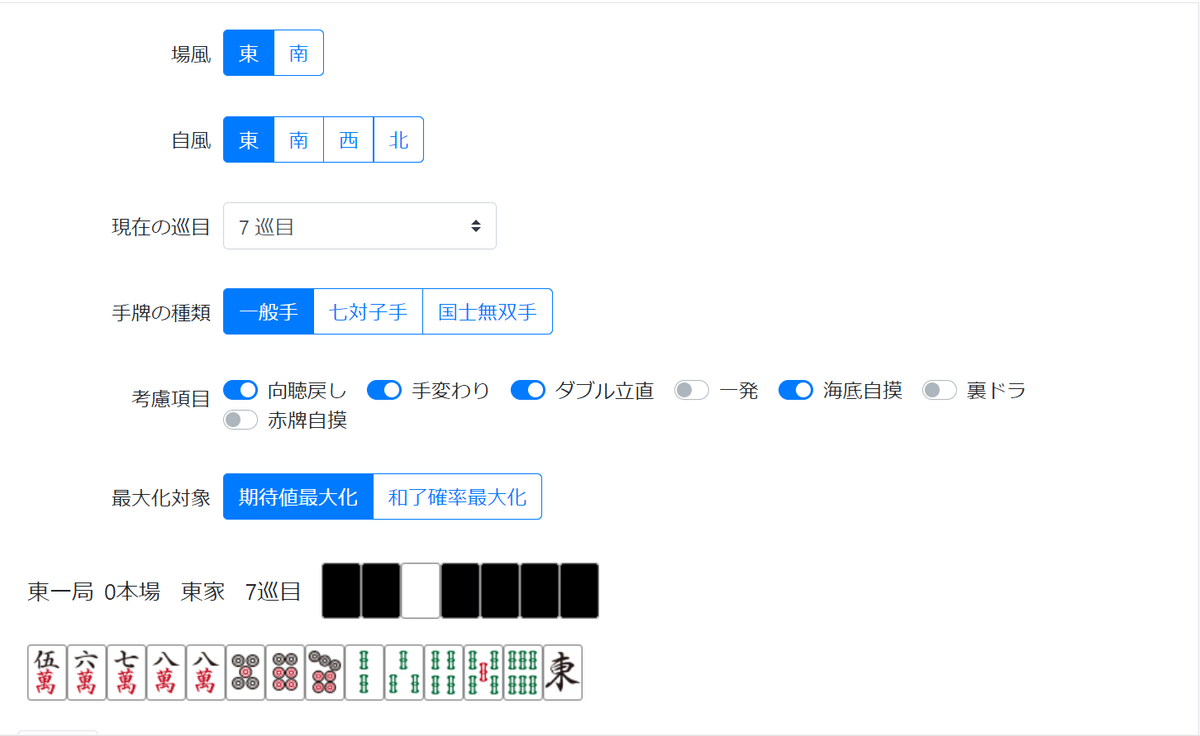
いつもお世話になっております。
1sが4枚残りの状態と、0枚残りの状態を両方解析し、それぞれの期待値を調べます。


なんと、1sが残っていないほうが期待値が高いという結果が出ました。1sツモをスルーする選択肢はありだと感じます。
…で終わるのは物足りないので、もう少し色々考えていきましょう。
考慮したいことは
①何巡目までならツモ牌をスルー出来るのか?
②ロン牌はどうか?
③一発裏ありはどうなの?
です。
ここから先は、分析を楽にするために楽な仮定を置いていたり、そもそも正しいか分からないのですが、大目に見ていただけると幸いです。
式が多いので、結論だけ読む方は目次から結論に飛んでお読みください!
①何巡目までならツモ牌をスルー出来るのか?事象を単純にして考える
まず①のツモ牌スルーを考えていきましょう。親なので、割と起こりうる次のような状況を仮定します。
「自分以外の3人は完全に降りていることが明らか」
「18巡目までツモり切り、流局時は1人テンパイになる」
この場合は、何切るシミュレーターとほとんど状況が同じになります。
1sをツモった場合、1300オールで3900点の収入+リーチ棒の1000点を必ず得られるので、期待値は4900点になります。
なので一旦、何切るシミュレーターに1s1枚切れの場合の期待値を計算させて、それが4900点を下回るタイミングを調べてみましょう。
(何切るシミュレーターはどうもリーチ棒収入を期待値に入れないようなので、3900点のタイミングを調べます)

このグラフを見る限りボーダーは14~15巡目にありそうです。これだけを見るとかなりスルー出来そうに感じますね。
さらに、何切るシミュレーターは流局時の収支を計算しません。
もう少しボーダー巡目が後ろに寄る可能性が高くなりそうです。
ここからは手動で計算します。
4sでアガると2600オールで7800点、7sでアガると6000オールで18000点になり、リーチ棒を回収するので、それぞれ1000点を加えます。
流局すると3000点の収支が得られて、次局に供託のリーチ棒を1/4で得られると考えると、流局の期待値は3250点になります。
流局率は(100%-アガリ率)です。
1sを全てスルーしたときの期待値は、
$${1s全スルーの期待値=(4sの和了率)×(7800+1000)+(7sの和了率)×(18000+1000)+(流局率)×3250}$$
となります。
47sは7枚あって、そのうち3枚、7sが4枚あるので、もう少し詳しくすると、
$${1s全スルーの期待値=(47sの和了率)×\frac{3}{7}×(7800+1000)+(47sの和了率)×\frac{4}{7}×(18000+1000)+(流局率)×3250}$$
となります。
これが4900点よりも大きくなる47sの和了率を求めます。
計算すると、11.59%より和了率が高ければ全スルーできるそうです。
ためしに1s全枯れの時の和了率を解析にかけてみると、

これが1sが全枯れの時のアガリ率グラフです。16巡目でもスルー出来るというとんでもない結果になりました。

本当かよと思って直近のNAGAをちょっと探してみました。たしかに残りツモ回数1回、他人からロンアガリ可能の3メンチャンの和了率が16.9%でした。9sの場況が良すぎるので何とも言えませんが、おおむね間違っていないと言えるのではないでしょうか。
①の結論
ここまでで、①の「ツモ牌は何巡目までスルー出来るのか?」という疑問は、「おそらく16巡目までスルー可能だろう」という一旦の答えが出ました。
②ロン牌だったらどうか?他家の動向を式に追加する
こんどは1sをロンアガリするときのボーダー巡目を考えていきます。
1sをロンすると2900点+リーチ棒1000点で計3900点の収支が得られます。
では先ほどの計算と同じように、見逃した時の期待値と収支の3900点が一致するタイミングを調べればいいのかというとそういうわけでもありません。
なぜなら、1sを打ってきている相手は大体危険牌を打ってきているので、必ずしも自分のアガリや1人テンパイになるとは限らないからです。仮に手詰まってそうとわかれば、①のツモスルーと大して変わらない結論がでるはずです。
そこで、先ほどの式に、失点の期待値と複数人テンパイのアガリ率を導入します。この値の導入が非常に厄介なので、ここからは私見と感覚がダダ入りになります。ご了承ください。
新たに導入した数を設定すると、1sを全てスルーするときの期待値は、
$${(1s全スルーの期待値)=(47sの和了期待値)+(流局時テンパイ料)-(失点期待値)}$$
このように計算することができます。
47sの和了期待値の計算式は①の前半部分で、
$${(47sの和了率)×\frac{3}{7}×(7800+1000)+(47sの和了率)×\frac{4}{7}×(18000+1000)}$$
です。
流局時テンパイ料は、
2人テンパイの時は1500+250=1750
3人テンパイの時は1000+250=1250
全員テンパイの時は250
これらをそれぞれ流局率と掛け算します。
全員テンパイの割合はかなり少なく、起きても250点しか期待値がないので、数値はかなり0に近づきます。なので一旦全員テンパイの期待値を無視します。
1人テンパイ率を50%
2人テンパイ率を40%
3人テンパイ率を10%
くらいにしておきましょうか。
失点期待値は、
『「統計学」のマージャン戦術』(みーにん(2017)、p16)
の「1500点~2000点」を使用し、今回はネガティブに「2000点」を採用します。連盟公式ルールなので実際はもうすこし1500点に寄った値を示すと思いますが、今回はどうネガティブに値を取っても見逃しを行えるラインを探します。
改めて7巡目の何切るシミュレーターのアガリ率を見てみると、

52.71%となっています。
この巡目に1sが出てきて見逃せるかを計算してみましょう。
『「統計学」のマージャン戦術』(みーにん(2017)、p26,31)
を参考にすると、
「流局率が15~20%」
と推測できます。
和了率を簡単に50%、流局率を20%にして計算を行うと、
$${(1s全スルーの期待値)=8800×\frac{3}{7}×\frac{50}{100}+19000×\frac{4}{7}×\frac{50}{100}+3250×\frac{20}{100}×\frac{50}{100}+1750×\frac{20}{100}×\frac{40}{100}+1250×\frac{20}{100}×\frac{10}{100}-2000}$$
となり、この期待値は5804.286点となります。ネガティブに和了率を10%程度減らしても、8巡目ならまだまだ余裕でスルー出来そうですね。
次に、12巡目を調べます。

アガリ率は38.21%です。
『「統計学」のマージャン戦術』(みーにん(2017)、p26,31)
を参考にすると、
「流局率は20~25%」
と推測できます。
アガリ率を35%、流局率を25%として計算を行うと、
$${(1s全スルーの期待値)=8800×\frac{3}{7}×\frac{35}{100}+19000×\frac{4}{7}×\frac{35}{100}+3250×\frac{25}{100}×\frac{50}{100}+1750×\frac{25}{100}×\frac{40}{100}+1250×\frac{25}{100}×\frac{10}{100}-2000}$$
この期待値は3732.5点になります。3900点よりも下の点数を示しましたね。
さすがに失点期待値が-2000点になることはないとは思うので、おそらく12巡目が局収支上のボーダー巡目だと思います。親の連荘にも500点ほどアドバンテージがあるでしょうし、12巡目に出た1sはロンアガリするほうが無難でしょうか。
しかも、7巡目に1sを打っている人は手が詰まって打たれている場合もありうるのに対し、12巡目の打1sはプッシュの方が割合として多くなります。自分の47s和了率をもう少し下に見積もっても良く、その瞬間ボーダーから下回るので、ロンあがりをした方が良さそうですね。
②の結論
ということで、②の結論は、
「1sプッシュをしてきている人がいた場合、見逃せるのは大体10巡目まで」
になりました。
③一発裏ありはどうなの?
②の結論から、一発裏ありのルールでは見逃せないし全部ツモしたほうがよさそうであることが分かると思います。本当にぎりぎり、一発を避けて出てきた7~8巡目あたりの1sを見逃すことができるくらいでしょうか。それでも自分で引いて来た1sはツモしたほうが良いと思います。
3ハンから4ハンになるという最大級の打点上昇を狙えるツモ裏1の2600オールは大きく、このチャンスをやすやすと捨てることはできないと思います。
①②③の補足
•この結果は7sの枚数にかなり依存します。7sが1枚でも見えているとスルーできる巡目が結構前になります。
・①の仮定を盤石にするために、リーチ後の河を全力で見て、ベタオリしているかどうかを確認する必要があります。かなり珍しい作業だと思います。
・①の仮定のもと、最高位戦classicルール(テンパイ料なし、アガリ連荘)では、親の連荘効率まで考慮して、何切るシミュレーターの期待値が5400点くらいを示すタイミングくらいまではスルー可能だと思われます。大体11巡目がボーダーラインですね。最高位戦classicルールでは、特に①の仮定を用いる局面が多いと思っています。
・②の計算を楽にするため、今回は1sを0枚としました。実際には、1sが出てきた後にもう一度1sを引いてきてツモあがるパターンもあるので、見逃した時の期待値はもう少し上になると思います。それでもボーダーが12巡目を超えることはなさそうに思えます。
・

今回の牌姿を少し変えたものになります。この場合は高めがすべて三色になりますね。ダマるかリーチするかの判断は一旦おいておくとして、これは12巡目でも見逃せるでしょうか?
計算式を省略して、12巡目の期待値が5262.5点でした。まだスルー出来そうですね。
今回の記事はここまでとなります!この記事を参考に、皆さまぜひよい見逃しライフをお送りください() 全国大会も頑張ります!
この記事が良いと思っていただけた方はぜひ記事の購入とスキ、Twitterでのシェアをお願いします!
参考文献
みーにん(2017)『「統計学」のマージャン戦術』、p26,31、竹書房
ここから先は
¥ 300
Amazonギフトカード5,000円分が当たる
もし何かためになることがありましたら、サポートして頂けると非常に有難いです!
