なぜ抑うつは指数分布に従うのか?
前回の話はこちら。
https://note.com/memantine2000/n/n253ad83e88e5
前回は抑うつスコアが指数分布に従うのことを説明した。今回は指数分布が成立する仕組みについて述べる。
#1 非時間軸の指数分布
指数分布といえば、時間を横軸とした指数分布がよく知られている。たとえば放射性物質の放射能の減衰は指数分布をしめす。統計学を勉強したことのある人なら、来店する客の時間間隔を思い出すと思う。このように、時間を横軸にする指数分布はよく知られている。その一方で非時間軸の指数分布はあまり知られていない(これまで統計学や医学の教科書で非時間軸の指数分布についての説明を見たことがない)。しかし、抑うつスコアの分布は非時間軸の指数分布なのである。
非時間軸の指数分布に従う現象を紹介する。例えば、気体分子の持つ運動エネルギーの分布や世帯別の金融資産の分布が挙げられる。それぞれの現象について簡単に説明したい。
大気中には大量の分子が飛び交っているが、それぞれの分子の持つ運動エネルギーは分子により異なる。少ししか運動エネルギーを持っていない分子が多く、大きな運動エネルギーを多く持つ分子は少ない。そして分子の持つエネルギー量の分布は指数関数に従う。ちなみにこの分布は物理学者ルートヴィッヒ・ボルツマンにより提唱されたので、ボルツマン分布と呼ばれる。
大気中には膨大な数の分子が存在し、それらは様々な方向にそれぞれの速さで運動している。そして大気中の分子同士が衝突を繰り返すことによって、分子の運動エネルギーは分子間で絶え間なく交換される。衝突が繰り返されることによってそれぞれの分子の持つエネルギー量が絶え間なく交換され、結果としてボルツマン分布が成立する。
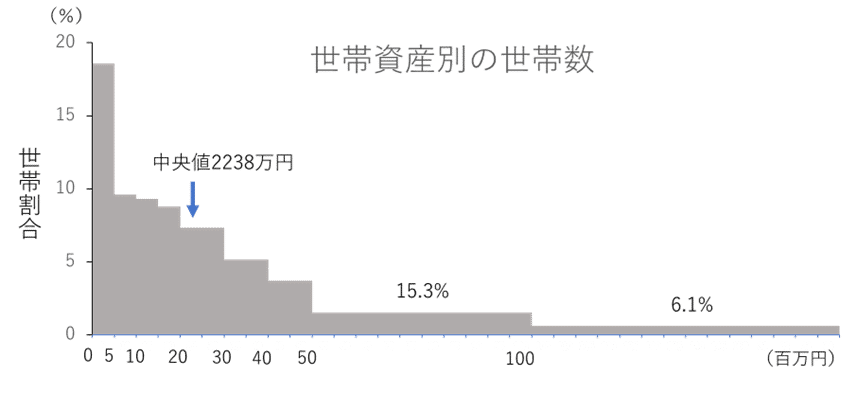
世帯別の資産の分布も指数分布を示すと言われている。図1は日本における世帯の純資産(金融資産や不動産や耐久消費財)の分布である。グラフがしめすように、世帯資産が500万以下しかないという世帯がもっとも多く、18.5%を占める。その一方で、純資産一億円以上の世帯は全体のわずか6.3%しかない。世帯資産が多くなるにつれ右肩下がりにその頻度が低下する。ちなみに日本の世帯別の純資産の中央値は2283万円である。
そしてこの右肩下がりの分布を調べると指数分布に近似する。なお世帯資産の分布は指数分布に従うが、資産がある程度以上に大きくなるとベキ分布に従うという説もある(Drăgulescu A. et al. Physica A 2001)。
現在社会においては常に個人や法人の間でお金が交換される(そういった交換を消費や商取引と呼ぶ)。そしてお金が絶え間なく交換されることにより、個々の世帯資産は指数分布を示す。
近年、世の中の経済格差に焦点が当てられることが多い。そういった貧富の格差が起きる要因として、教育格差や人種格差が指摘される。しかしエントロピーの法則から考えると、仮に同じ条件からスタートしたとしても、金銭の絶え間ない交換が続けば、必ず指数分布つまり貧富の格差が出現する。
分子の運動エネルギーや世帯の資産はまったく関連のない現象に見える。しかし、これらの現象はいずれも同じルールによって成り立つ。結果として、これらの現象は指数分布をしめす。
非時間軸の指数分布が発生する仕組みについて説明する。最初に結論を述べると、非時間軸の指数分布は絶え間ない交換によって発生する。何らかの数量が担体の間で絶え間なく交換されると、その担体における数量の頻度は指数分布となる。なお担体とは、その数量(たとえば運動エネルギーやお金)を担うものである。
一方、正規分布は様々な要因の足し算(和)によって生まれる。身長は正規分布に従うことが知られているが、それは様々な影響(栄養、様々な遺伝子、生活スタイル)の和によって身長が決まるからである。世の中に正規分布にしたがう現象が多いのは、影響の和によって成り立つ現象が多いからだである。
正規分布に従う指標の場合、何らかの数量を交換することはない。たとえば身長を個人間で交換したりはしない。正規分布では様々な要因の足し算によって成立する。正規分布と指数分布では、仕組み、形、性質が異なるのである。
では前述した仕組むによって本当に指数分布や正規分布が発生するか、シミュレーションによって検証してみたい。
#2 シミュレーションによる正規分布の発生
まず、影響の足し算によって正規分布が発生することをシミュレーションしてみる。
足し算のシミュレーションとしてはジャンケンによるゲームを想定する。ゲーム参加者はディーラー(胴元)とジャンケンを行う。ジャンケンに勝てば参加者は1枚コインがもらえるし、負けた場合はもらえない。なお負けても参加者の手持ちのコインを渡す必要はない。つまり参加者の手持ちのコインは増えるだけで減るのことないゲームである。ジャンケンの勝率は5割とする。
100名のゲーム参加者がそれぞれのディーラーとジャンケンを行う。参加者がそれぞれ40回ジャンケンをしたら手持ちのコイン数がどうなるかをシミュレーションしてみた。その結果が図2Aである。手持ちのコインの分布は釣り鐘型の正規分布に近い形となった。

(A)はディーラーとのジャンケンを40回行った時の分布。
(B)は参加者同士のジャンケンを6000回行った時の分布。
(C)は参加者同士のジャンケンを4万回した時の分布。
40回のジャンケンの結果を見ると、20枚前後コインを手に入れた人の頻度が最も多かった。これはジャンケンの勝率が5割だからである。コインを30枚以上持つ、あるいは10枚以下しか持たない人はほとんどいなかった。
手持ちのコインの分布が最終的に正規分布に近い形(対称で釣り鐘型)になったのは、手持ちのコインの数は40回行われたジャンケンの結果の足し算だからである。様々な影響の総和によって決まる現象は正規分布に従うのである。
次に絶え間ない交換により指数分布が出現するかどうかを検証した。絶え間ない交換のシミュレーションでは、参加者同士でジャンケンを行い、勝った人は負けた人からコインを1枚もらう。誰と誰がジャンケンをするかについては抽選で選ばれる。
このシミュレーションの特徴は、ジャンケンの相手がディーラーではなく、参加者同士ということである。つまり参加者同士が勝負することによってコインが参加者内で絶え間なく交換されることになる。当然、手持ちのコインが増える人もいれば少なくなる人もいる。図2Aの状態から引き続いて、参加者同士のジャンケンシミュレーションを行った。
参加者同士のジャンケンを続けると、負けが続いて手持ちが0枚になる参加者が出現する。0枚になっても参加者はゲームに参加することができる。その代わり、もし手持ち0枚の人が負けた場合は、相手にコインを払う必要はないし、相手もコインをもらえない。つまり手持ちのコインが減ってもマイナスになることはない。こういったルールでゲームを継続する。すると分布の形はどうなるのだろうか?
図2Bはジャンケンを総計6千回行った時点でのコインの分布である。図2Aに比べて、分布の頂点が低下し、ばらつきが左右に広がっているのがわかる。ばらつきが左右に広がるのは、勝ちに恵まれる人もいれば、負けが続く人もいるからである。回数を重ねるほど手持ちのコインの数のばらつきが大きくなる。これはコップにインクを一滴入れると時間ととも広がる現象に似ている。
図2Cはジャンケンを総計4万回行った時の分布である。見てわかる通り、右肩下がりの分布が出現している。矢印が示すように手持ちのコインが0枚の人が一番多く、手持ちのコインの数が増えるほどその頻度は右肩下がりに減少する。そしてこの分布の形を調べると指数分布に近似することが確認できた。なおこの後ジャンケンを続けても、分布の形が変わることはなかった。以上より、絶え間ない交換を継続すると指数分布が成立することが確認できた。
シミュレーションの結果、参加者同士でコインを交換するジャンケンでは指数分布が出現することが明らかになった。ではなぜ参加者同士でジャンケンを繰り返すと右肩下がりの分布が出現するのだろうか。
前述したように、参加者同士のジャンケンを続けると、勝ちに恵まれる人と負け続ける人の間で差が広がっていく。6千回までは分布のバラツキは両方向に対称的に広がっていた(図2B)。しかしこのゲームのルールでは、参加者の手持ちのコインの数がマイナスになることはない。その結果、次第に手持ちのコインの数が0枚や1枚といった人々が“溜まる”ことになる(図2Cの矢印)。したがってここが分布の頂点となる。
その一方で、分布の右端には、ジャンケンに勝つ機会に恵まれた少数の人々が存在する。しかし、こういった人々のコインが永遠に増えるわけではない。なぜなら参加者全員のコインの総量は変わらないからである。そうなると、手持ちのコインの数が少ない人々とコインを多く持つ人々の間にバランスが生じる。そしてこのバランスが、最終的に指数分布を生むことになる。
絶え間ない交換によって指数分布が出現する仕組みについては、エントロピー最大化の原理によって説明することができる。エントロピーは熱力学や情報学といった様々な分野で使われる概念であり、乱雑さと訳されることが多い。エントロピー最大化を確率の視点から定義すると、最も起こりうるでよいと思う。個々の担体の間で絶え間なく交換が行われると、確率的に最も起こりうるのは(エントロピーが最大となるのは)指数分布なのである。
エントロピー最大化によって指数分布が生じる仕組みについて詳しく知りたい人は、生物物理学者の大澤文夫によって書かれた入門書があるので、そちらを参照してほしい(大沢文夫 2011 名古屋大学出版会)。
ところで図2Aや図2Cのグラフは正規分布や指数分布に似ているが、ざっくりとしか似ていない。参加者数や最初のジャンケンの回数(胴元と行うジャンケン)を大幅に増やせば、もっと正規分布や指数分布に近い分布を観察することができる。しかし私のパソコンの性能ではこのあたりが限界である。高性能パソコンをお持ちの方は、参加者数や最初のジャンケンの回数を大幅に増やしてシミュレーションしていただくと、より正規分布や指数分布に近い分布を観察することができる。
#3 抑うつは交換されるのか?
抑うつスコアの分布が指数分布に従うということは、抑うつは絶え間ない交換の仕組みによって成立するということである。しかし抑うつは交換されるものなのだろうか?この点について考えてみたい。
たとえば金銭の場合、金銭が交換される現場を実際に確認することができる。金銭には貨幣という実体が存在するからだ。したがって誰と誰がどこでどれくらい金銭を交換したかを追跡できる。しかし抑うつという心理現象には貨幣のような実体がない。したがって誰と誰がどこで抑うつを交換したかを確認できない。それにもかかわらず、世の中を観察すると抑うつが交換されているかのように見える機会は多い。
たとえばある人が難関大学に合格したとする。当人にとって、希望の大学に合格したことはうれしいと思う。しかし誰かが難関大学に合格したということは、他の誰かが不合格になるということである。合格した人は喜ぶが、不合格になった人は抑うつ的になる。当人同士は気づいていないが、結果的には抑うつが交換されるように見える。
こういった誰かが何かを得ると誰かが何かを失うという関係をトレードオフの関係と言う。トレードオフの関係は社会の至る所で観察できる。ある企業が成長すれば、ライバル企業の経営は厳しくなる。あるプロ野球選手が活躍してレギュラーになれば、誰かが退団となる。異性から非常に人気がある人が存在するということは、あまり人気のない人が大量に生まれるということである。
社会では様々な状況にトレードオフの関係が存在する。そして数えきれないトレードオフの関係によって無意識に抑うつが絶え間なく交換されるのかもしれない。
もちろん人間社会は競争だけではなく、協力によっても成り立つ。ビジネス、家庭、公的扶助、いずれも協力なしでは成り立たない。しかし協力するということは、利益や負担を分かち合うということである(例えば北欧のような充実した社会保障を行うには消費税を高くする必要がある)。そして利益や負担を分かち合うということはトレードオフの関係と見ることもできる。
協力と競争は対義語であり、反対の概念として扱われる。協力では両者の目的が一致しているが、競争では相反している。しかし最終的にはどちらも利益や負担を分配する。つまりトレードオフの関係と見ることもできる。
#4 相対評価とトレードオフ
抑うつの交換が行われるもう一つの仕組みとして、相対評価がある。人は無意識に相対評価の影響を受けている。そうなると結果的にトレードオフの関係が成立することになる。
なぜ相対評価がトレードオフの関係を生むのかを説明したい。
たとえば同じ小学生でも運動会の徒競走が楽しみという子もいれば、憂うつな子もいる。足が速い小学生にとっては、徒競走は活躍の場であり、楽しみだろう。逆に走るのが遅い子にとっては、徒競走はストレスと思う。
この場合、足が遅いという認識は、クラスにおける相対評価に基づく。そして相対評価を基準にすれば、足の遅い子はクラスの中にある程度の割合で存在する。つまり単純に考えると、全国の小学生の中で徒競走をストレスと感じる子はある程度の割合で存在することになる。もちろん中には足が遅くても徒競走が大好きな子も存在するかもしれない。しかしここでは話を単純化して進めたい。
小学生の足の速さも年齢と共に変化する。客観的な足の速さ(絶対評価)なら、ほとんどの小学生は学年が上がるに連れ足が速くなる。絶対評価によって徒競走のストレスが決まるなら、年齢とともに足の速さで悩む子は減少するはずである。しかし現実はそうならない。年齢と共に足が速くなっても、クラスの中での順位が下位だとやはり悩みは続く。
成長するにつれ足の遅い子が速くなることもあるだろう。本人にとってはうれしいと思う。しかし相対評価の場合、誰かの順位が上がれば誰かの順位が下がる。つまり個人は入れ替わるが、足の遅い子はクラスの中に必ず一定の割合で存在する。人が相対評価に影響される限り、トレードオフの関係が生まれ、結果的に足の遅さで悩む子が一定の割合で存在する。
小学生の足の速さを例に説明したが、中学生になればさすがに徒競走への関心は薄れるだろう。その代わり中学生は容姿や学力やコミュニケーション能力を気にするようになる。そうなると、容姿や学力やコミュニケーション能力が相対的に低い中学生はそのことで悩むことになる。そして大人になれば仕事の能力や人間関係や金銭面で悩むようになる。つまりどの年代でも人は相対評価の影響を受ける。心理社会学者であるフェスティンガーは「人は自身を他者と比較する基本的衝動を持っており、比較を通して自身を評価する」と述べている(Festinger L. Human relations 1954)
人は無意識に相対評価の影響を受けると説明すると、異を唱える方もいるのではないかと思う。「私は自らの感性や理性に基づいて物事を判断しており、相対評価などしていない」と反論する方もいると思う。しかし無意識に人は相対評価を行っている。
たとえばテレビ視聴者がある俳優をハンサムと感じたとする。一見これは相対評価とは無縁の判断に見える。その俳優を特定の誰かと比較してハンサムと判断したわけではないからだ。しかし容貌を判断するにはそのための尺度が必要である。
おそらく容貌を判断するための尺度は、その人がこれまで得た容貌に関する莫大な情報によって成り立つ。そしてもしその俳優の容貌が一般人に比べて大差なければ(これは相対評価である)、テレビ視聴者はその俳優をハンサムと認識することはないだろう。つまり人は容貌を評価するための尺度を使用することによって、無意識に相対評価の影響を受けるのである。そして人間のストレスの認識が相対評価に強く影響されるのなら、ストレスの絶え間ない交換が行われることになる。結果として抑うつのスコアの分布は指数分布に従うのかもしれない。
文献
1)Drăgulescu A. et al. Exponential and power-law probability distributions of wealth and income in the United Kingdom and the United States. Physica A: Statistical Mechanics and its Applications.2001 299: 213-221.
2)大沢文夫 大沢流 手づくり統計力学 2011 名古屋大学出版会
3)Festinger L. A theory of social comparison processes. Human relations, 1954 7: 117-140.
