抑うつ症状の分布の数理パターン
今回は、抑うつ症状の大規模データを観察した結果、分布の数理パターンが見つかった話である。
#1 日本における抑うつ症状の分布
抑うつ症状とは、抑うつにともなって心身に現れる様々なのことである。抑うつ気分、不安、意欲の低下、自殺念慮といった心理的なものから、不眠、食欲低下、疲労感といった身体的なものまで様々なものがある。
世の中にはこういった症状をまったくもたない人もいれば、軽い抑うつ症状を時々認める人もいる。中には重い抑うつ症状が毎日のように続く人もいる。
では社会における抑うつ症状の分布はどうなっているのだろうか?抑うつ症状が重い人は軽い人よりも少ないとは思うが、それはどういった分布に従うのだろうか?
実は抑うつ症状の分布の数理モデルに関する論文を調べたが何もなかった。
そこで「保健福祉動向調査」のデータを使って抑うつ症状の分布を調べてみた。
保健福祉動向調査とは日本で初めて行われたメンタルヘルスに関する大規模行政調査である。厚生労働省によって2000年に全国32022人を対象に行われた調査である。調査対象は国勢調査の人口統計に基づいて全国から抽出された。ちなみに分布の数理モデルを調べる場合、数百人程度のデータでは分布の形が不安定なので難しい。保健福祉動向調査対象は3万人を超えるのでサンプル数としては十分である。
保健福祉動向調査では抑うつ症状のレベルを測定するためにCES-Dという抑うつ評価尺度が使われた。CES-Dでは、被験者は、過去1週間に抑うつ症状がどの程度をあったかを、「ほとんどない」「少しある(1-2日)」「かなりある(3-4日)」「いつもある(5日-7日)」の4つ選択肢から選ぶ。なおCES-Dは抑うつ症状16項目とポジティブ感情4項目の総計20項目の症状で構成される。
保健福祉動向調査のCES-Dの抑うつ症状16項目の抑うつ症状の分布を図1に示す。

図1を見ると、抑うつ症状の分布は症状によってかなり異なることがわかる。例えば、「6.何事も面倒だ」という項目では、45%の人が「ほとんどない」と答えているが、「13.突然泣いてしまう」という項目の場合、92%の人が「ほとんどない」と答えている。「6.何事も面倒だ」のように半数以上に認められる症状もあれば、「13.突然泣き出してしまう」のようにかなり少ない症状もあるということである。
「9.不眠」に対しては、全体の三分の一が多かれ少なかれ症状を認めている。しかしだからといって日本人の三人に一人が不眠症と診断されるわけではない。不眠症の診断基準(DSM-5)では不眠を週に3日以上認めることを診断項目にしている。現在の精神医学では週に1-2回程度の不眠を病気とは診断見なさないということである。
また抑うつ症状の分布には共通点もある。過去一週間の抑うつ症状の程度に対して、すべての項目で「ほとんどない」を選択した人が一番多く、「少しある(1-2日)」「かなりある(3-4日)」「いつもある(5日-7日)」と症状が重くなるにつれ頻度が少なくなる。
では抑うつ症状の分布に共通する数理パターンは存在するのだろうか?
おそらく図1を見ただけで、そこに存在する数理パターンに気づく人は少ないと思う。私も初めて図1を見た時には気づかなかった。しかし、図1のグラフには確かに数理パターンが存在する。そしてそれに気づくには、「折れ線グラフ」が必要となる。
#2 抑うつ症状の分布の折れ線グラフ
図2は図1の棒グラフを折れ線グラフにしてすべて重ね合わせたものである。

図2の16本の線グラフを見ると、そこになんとなく共通するパターンが存在することに気づくのではないかと思う。
ちなみに筆者がこのグラフを初めて見た時はかなり興奮したことを覚えている。こんな幾何学的なパターンが現れると予想していなかったからだ。ナスカの地上絵を初めて見つけた人はこんな気分だったのかもしれない。
図2のグラフに共通するパターンの特徴を述べる。まず「ほとんどない」と「少しある」の区間において、すべてのグラフがほぼ同じ交点(矢印)で交差している。一方「少しある」から「いつもある」までの区間においては、いずれのグラフも低下している。この低下の仕方にはなんとなく規則性があるように思える。実は「少しある」から「いつもある」の区間では、すべてのグラフがほぼ同じ比率で変化している。
「かなりある」から「少しある」への減少率を計算すると、16項目の平均が0.32、標準偏差が0.06となった。また「かなりある」から「いつもある」への減少率も、平均が0.45、標準偏差は0.09となった。つまり「少しある」は「かなりある」の約三分の一に減少し、「いつもある」は「かなりある」の約四分の一に減少するということである。
標準偏差がそれぞれ0.06と0.09といういう小さな値となったということは、「少しある」から「いつもある」までの区間の減少率のグラフ間のバラツキが低いことを示している。
#3 抑うつ症状の分布モデル
明らかになった抑うつ症状の分布の数学的特徴から、その数理モデルを作成してみる。このモデルの特徴は、すべての抑うつ症状において「少しある」から「かなりある」への減少率と「少しある」から「いつもある」への減少率が等しいということである。
図3Aに示すように、「少しある」の確率をPとし、「少しある」から「かなりある」への減少率をr1, 「かなりある」から「いつもある」への減少率をr2とした場合、「かなりある」と「いつもある」の確率は、それぞれP×r1、P×r1×r2となる。また、すべての選択肢の確率は100%なので、「ほとんどない」の頻度確率は1-(P+Pr1+Pr1r2)となる。
図3Bは二つの抑うつ症状の分布のモデルである。「少しある」の確率をそれぞれP1とP2と仮定したものである。図2と図3Bのグラフを比べると、実際の分布(図2)が抑うつ症状の分布の数理モデル(図3B)と非常に似ていることがわかる。
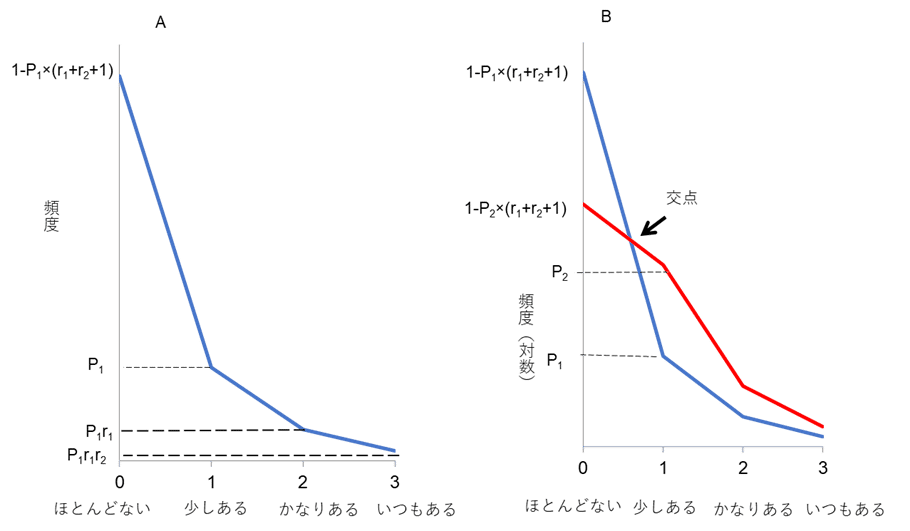
ちなみに図3のモデルを使って、「ほとんどない」と「少しある」の間の交点の座標を計算すると、(x, y) = {(r1r2 + r1 + 1)/(r1r2 + r1 + 2), 1/(r1r2 + r1 + 2)}となった。この交点はr1とr2だけで構成されているので、Pの値に左右されない。よってこのモデルを想定すると、抑うつ症状のすべての線グラフが「ほとんどない」と「少しある」の間の一点(前述した座標)で交わることが証明できた。
これまで一般人口の抑うつ症状の分布の数理モデルが報告されたことはなかった。また統計学の専門家にも相談してみたが、そもそも図3のような分布モデルを見たことがないとの返事だった。しかし分布モデルの名称がないと話を進めづらい。したがって、抑うつ症状の分布モデル(図3)を「DS分布」(Depressive symptom distribution)と呼ぶことにする。
科学において再現性を確認することは重要である。これまで日米欧の大規模データを用いてDS分布の再現性を確認した。その結果、抑うつ評価尺度の種類や国や時代に関係なく、DS分布の再現性を確認できた(Tomitaka.Heliyon 2020)。これまでのところ確認できなかったデータはない。この現象の再現性は高いと思われる。
#5 DS分布が見過ごされてきた理由
それにしてもなぜDS分布はこれまで報告されてこなかったのだろうか?。
現在、先進国ではメンタルヘルス問題が大きな社会問題となっている。そういったこともあり、どの国でも抑うつ評価尺度を用いた大規模な疫学調査が行われている。そしてその結果は膨大な数の論文や報告書として公表されている。
つまりこれまで様々な国の多数の専門家が抑うつ症状の分布のデータを解析したということである。そして私がそういった調査結果を解析したところいずれもDS分布を確認できた。にもかかわらず、これまで抑うつ症状の分布の数理パターンが報告されたことはなかった。これは不思議としか言いようがない。
これまでDS分布が報告されなかった理由について考えてみた。まず考えられるのは、DS分布は新規で複合的な数理パターンであったことが考えられる。複合的とは、選択肢の場所によって分布の数理パターンが異なるという意味である。たとえばCES-Dの場合、DS分布は選択肢「少しある」の左右で分布関数が異なる。
分布の数理パターンを調べるには、一般的に既存の分布モデルのあてはめ(curve fitting)を行う。既存の分布モデルとは、たとえば正規分布や指数分布のことである。しかし抑うつ症状の分布に既存の分布モデルをあてはめてもDS分布に気づくのは難しい。DS分布は新規のモデルだからだ。そういったこともあり、DS分布はこれまで見過ごされたのかもしれない。
さらにもう一つの理由として、統計学の常識が関係しているのかもしれない。実は統計学において、抑うつ症状のようなデータをグラフ化する場合、図1のように棒グラフを使用する。それが慣例である
統計学では抑うつ尺度のようなデータは「順序尺度」に分類される。順序尺度とは尺度に順序は存在するが、等間隔性が保証されていないものをいう。そして順序尺度から得られたデータをグラフ化する場合、線グラフではなく、棒グラフを使用する。
実際、統計ソフトを使って順序尺度のデータを分析すると、自動的に棒グラフが表示されるようになっている。しかし棒グラフには短所もあり、複数のグラフを一枚のグラフに重ね合わせることができない。抑うつ症状の分布に共通する数理パターンに気づくには、線グラフの重ね合わせ(図2)を行う必要があった。つまり統計学の慣例を無視する必要があった。
線グラフの重ね合わせは非常に単純な作業である。数理モデル研究の手法として専門書で紹介されるようなものではない。しかし、DS分布に気づくには線グラフの重ね合わせが必要だったと思われる。
文献
1)厚生労働省大臣官房統計情報部編 平成12年保健福祉動向調査 2002厚生統計協会
2)Tomitaka S. et al. A distribution model of the responses to each depressive symptom item in a general population: a cross-sectional study. BMJ open 2015 5: e008599.
3) Tomitaka S. Patterns of item score and total score distributions on depression rating scales in the general population: evidence and mechanisms. Heliyon. 2020 6: e05862.
