【統計】サイコロを180回投げて1の目が40回以上出る確率【🎲】

よし、これ反復試行の確率やん

もーらいっ

どん

無理です。すみません。

こんなときは統計の手法を使おう！

使うのはドーン！

二項分布

B(n,p)

今回はn=180(試行回数), p=1/6(サイコロを振って1の目が出る確率)ですね。

B(180,1/6)

こやつの期待値と分散は以下の式

期待値

E(x)=np

分散

V(x)=np(1-p)

から求められるので

E(x)=180・1/6=30

V(x)=180・1/6・5/6=25(=5^2)

です。

試行回数n=180は十分に大きく正規分布に近似できるので(唐突)

正規分布

N(μ,σ^2)

のμ(期待値)に30、σ^2(分散)に25=5^2を突っこみます

どーん

N(30,5^2)

ここでみんなお楽しみのz変換(標準化)します。

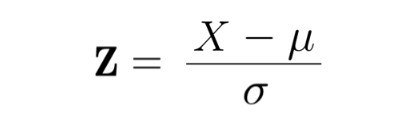
キラン

Z=(X-30)/5

これでZは平均0、分散1の正規分布N(0,1)(標準正規分布)に従います。やったね。

求めたいのは1の目が40回以上出る確率ですので、X=40を代入します。

するとZの値は

Z=(40-30)/5=2.00

そして標準正規分布の確率を表で確認すると

Zが2.00以上になる確率は0.0228

つまり2.28%

よってサイコロを180回投げて1の目が40回以上出る確率は2.28%です。

期待値は30回なので40回ってそんなに珍しいことではないんじゃね(例えばサイコロを18回投げて1の目が4回以上出る確率は26.76%)、と思いましたがかなり珍しい事象ということが分かりました。

やっぱり

確率は収束しますね(キラン

言ってみたかっただけです。

お疲れ様でした。

以上です。