
補足編 薄翼理論の数学
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第65回目として「薄翼の理論」について紹介する予定です。そこで,補足編の「薄翼理論の数学」と題して,薄翼理論を勉強するためだけに必要な数学を取り上げます。具体的には,三角関数とフーリエ解析の2つを紹介していきます。
(1)三角関数
(1-1)還元公式
はじめに,三角関数の還元公式からいきましょう。還元公式とは何ですかと思われる方もいらっしゃると思いますが(筆者も公式集を調べる前まで同意見),いわゆる90°(π/2),180°(π),270°(3π/2)を角度θに加算,減算した公式のことを指します。そのため,単位円(半径1の円)を考えることが出来れば,図1~図5のような単位円および公式が成立します。





今回は,便宜上sin,cos,tanの3つを書いていますが,必要なのはsin,cosの2つのみなので,tanはおまけであり,270°(3π/2)については使わないので省略します。
(1-2)加法定理
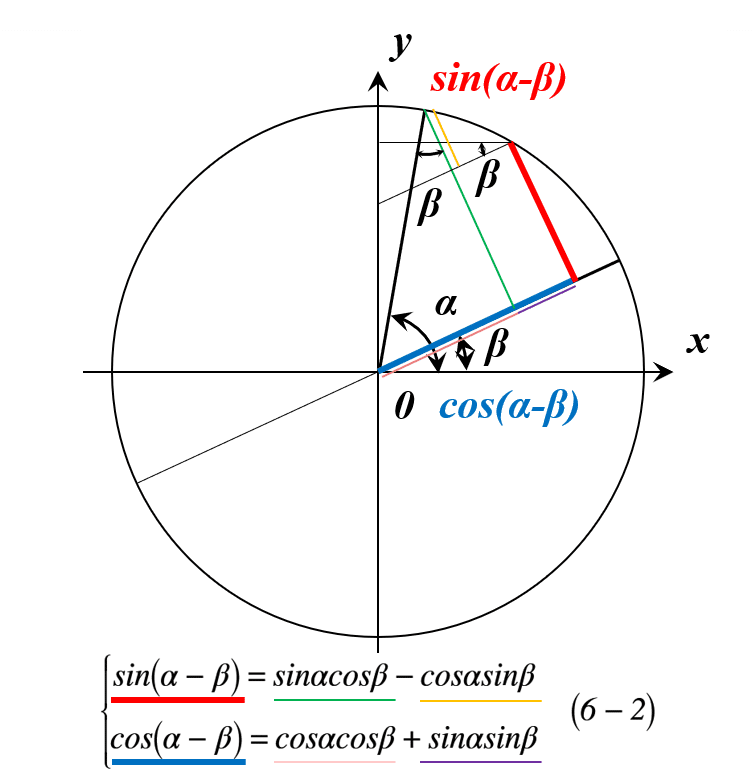
次に,三角関数の加法定理を導出してみましょう。ちなみに,1999年の東大入試で加法定理の導出が出題されて話題になりましたね。導出といっても結局のところ,単位円を使って出すだけなので,あとは他の解説しているネタの方々に譲りたいと思います。ポイントがあるとすれば,角度βを別の場所に描いて角度αの整合性を保つように線分を求めなければならないことでしょうか。 図6-1,図6-2に単位円および公式を示します。

(1-3)積和公式
次に,積和公式を導出してみましょう。先ほどの加法定理のように単位円を使った幾何学的な求め方でもできますが(図形的なイメージが出来ていることが最も望ましい),結局のところ,導出結果を使ってナンボなので,加法定理から代数的に解いて算出しましょう。

基本的には,加法定理を加算,減算するだけで求められるので,式(7)のようにまとめられます。

ちなみに,これも受験生版タイガーファンディングでとある開業医の方が受験生に質問して話題になっていましたね。あれも2年前の出来事とは…。
(1-4)定積分
次に,定積分を導出してみましょう。ちなみに,今回の定積分は「薄翼の理論」の途中で出てくるもののみを抽出しています。求めたい定積分は以下の6題です。
① 定積分problem1

忌まわしき定積分です。この定積分は一端「不定積分」として考えることが重要です。分かりづらい積分を解くときの常套手段ですね。皆様は,この積分をすぐ解けますか?ちなみに,筆者自身はこの積分に1日かかりました。(泣)

キングプロパティでも三角関数の有利化でもなく,三角関数の加法定理,積和公式とθの分解を使ってゴリ押しして解くという,かなりトリッキーなやり方で解きました。(これ以外のスマートな解き方がある不特定多数の皆様は是非教えてください。)

実は,対数関数の積分形式となるので,意外ときれいな形にはなりますが,結局のところ,定積分にしたときは「ゼロ」になるので関係ないですね。
② 定積分problem2

①の定積分とあまり変わりません。ここで筆者自身は何を血迷ったか,この積分にキングプロパティでも三角関数の有利化を適用しようしてど壷にはまりました。結局,2日も無駄にするバカな筆者です。(泣泣)

ここでも,三角関数の加法定理と積和公式をゴリ押しして解くやり方で解きました。θとθ1が混在しているので,別々の変数であるという認識が抜けやすいのが注意点でしょうか。
③ 定積分problem3

②の定積分とどこが違うのかわからないほど変わりません(cosθはcosnθになりました。)。先ほどと同様,筆者自身は何を血迷ったか,この積分にキングプロパティでも三角関数の有利化を適用しようしてど壷にはまりました。結局,更に1日無駄にするどうしようもない筆者です。(泣泣泣)
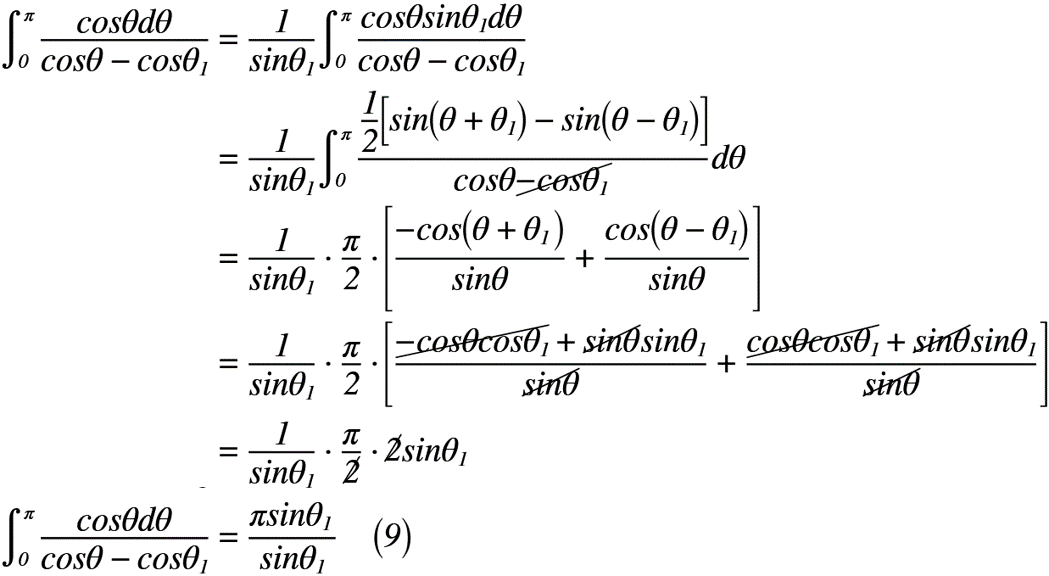
ここでも,三角関数の加法定理と積和公式をゴリ押しして解くやり方で解きました。sin,cosの積分時に+と-の符合が混同しやすいのが注意点でしょうか。
④ 定積分problem4

③の定積分にあるcosからsinに変わっただけです。さすがにここまでくると,三角関数の加法定理と積和公式をゴリ押しして解くやり方で解けることを理解した筆者は,無難にこなせるようになりました。三度目の正直とは,まさにこのことでしょう。(笑)

sinの加法定理は符合のズレが少なくなる傾向なので,計算ミスしにくいので大変助かります。実は,この定積分が一番はじめに解けたのは秘密です…。
⑤ 定積分problem5

毛色の異なる積分になりました。解析学で特に,フーリエ変換に触れたことのある理系の方々はおそらく一度は目にしたことがあるのではないでしょうか。奇関数と偶関数の区別をするのによく用いられる考え方です。

大学の教科書,参考書に記載があるのは周期2πの場合が多いとは思います。結局のところ「ゼロ」になるので,式の形がどうであっても関係ありませんね。
⑥ 定積分problem6

難易度順に並べている訳ではありませんが,難易度でいえば一番簡単な定積分でしょう。

今回,(ここでしか使わなかった)三角関数の半角公式の導出を見送りましたが,いわゆる三角関数の公式(倍角,半角,積和,和積,合成など)を使った定積分は大学受験でも,大学・高専の定期試験でも頻出でしょう。
(2)フーリエ解析
(2-1)フーリエ余弦級数
一般的なフーリエ解析の講義で取り扱う内容は「級数」と「変換」の2種類ですが,今回は「級数」のみを取り扱います。最初は,sinとcosの2つを組み合わせて,図7のような周期的に簡単な2πのフーリエ級数を取り扱います。

その後,奇関数の場合は,sinのみを考えればよいため「フーリエ正弦級数」となり,一報で偶関数の場合は,cosのみを考えればよいため「フーリエ余弦級数」となり,図8のような関数はこれを使用できます。

薄翼の理論は,主に「フーリエ余弦級数」のみを取り扱うことになるため,グラフの外観は偶関数で表せることを意味しています。
(3)まとめ
今回の記事のまとめを以下に示します。
① 薄翼理論の数学は,三角関数とフーリエ解析の2つを主に用いる。
以上です。最後まで閲覧頂きありがとうございました。
本記事は,「薄翼の理論」にて利用する背景知識となります。
いいなと思ったら応援しよう!

