
流体力学 渦周りのポテンシャル流れ(その1)
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第37回目は,前回の予告通り「渦周りのポテンシャル流れ」について紹介していきます。
(1)渦周りのポテンシャル流れについて
では,「渦周りのポテンシャル流れ」について,解説していく訳ですが,連載企画となります。最近の筆者自身の流行りという訳でもありませんが,以下に解説していく順番を示します。
(ⅰ)強制渦
(ⅱ)自由渦
(ⅲ)原点より半径における圧力変化
(ⅳ)2次元流れにおける中心静圧p
(ⅴ)渦周りの複素ポテンシャル
(ⅵ)渦周りのポテンシャル流れの応用例(ビオ・サバールの法則)
渦については,過去の記事にて紹介していますので,気になる方はチェックしてみて下さい。
今回以降の記事は,数学的な議論がメインとなります。そして,「渦周りのポテンシャル流れ(その1)」では,(ⅰ)強制渦と(ⅱ)自由渦を主に取り上げていきます。
(2)渦周りのポテンシャル流れとは?
主題でいきなり出てきた言葉の定義を説明します。これは,2次元流れ中の任意のある1点を中心として,半径aの渦管と循環Γがある場合を想定して,渦管内外における周速度がある流れを示します。煩雑な説明でしたが,図1のような流れ場になります。

図1 渦周りのポテンシャル流れ
この流れ場をベースにすべての解説をしていきます。次項では,早速「強制渦」について説明していきます。
(3)渦管内で流体が剛体のように形を崩さない回転をしている渦(強制渦)
では,本格的に証明してみましょう。以前の記事でも紹介していますが,強制渦は流体微小要素が剛体のように形を崩さない回転をしている渦を示します。そのため,図2のような速度分布となります。
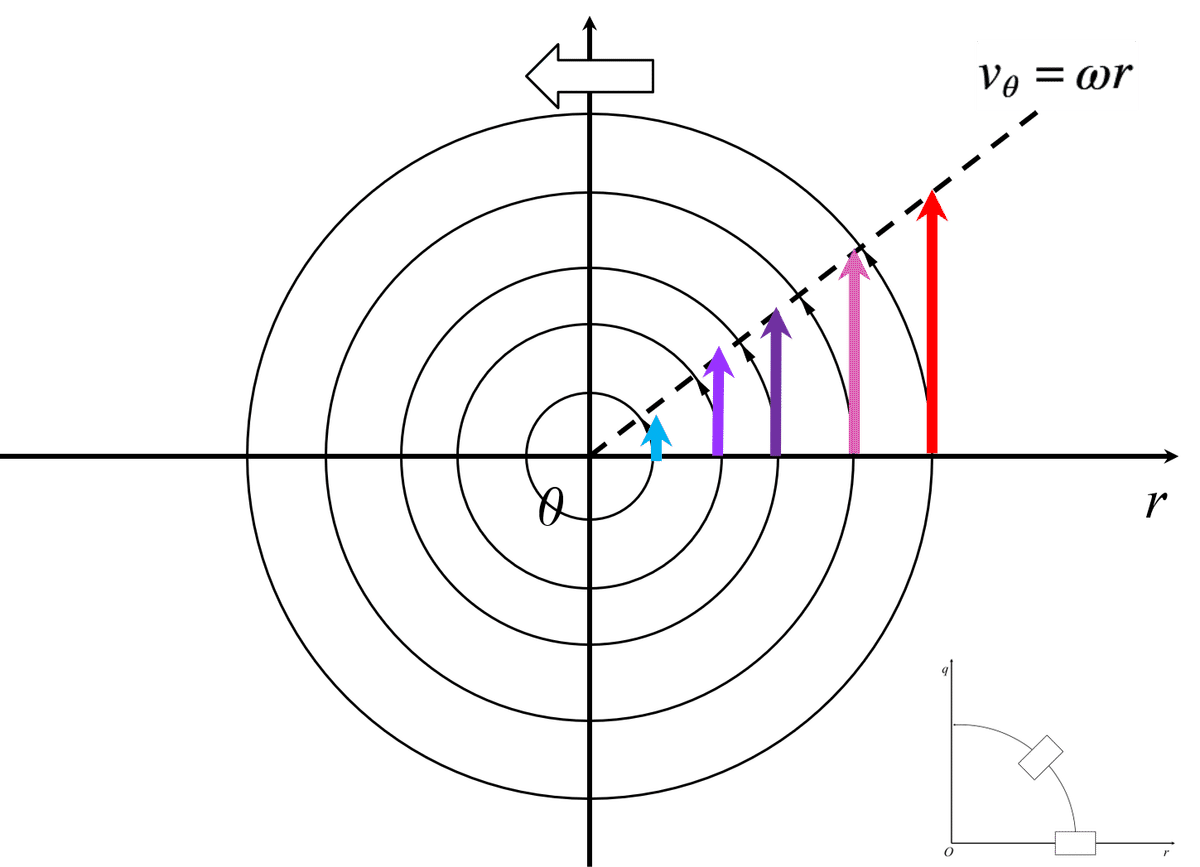
図2 強制渦の速度分布
よって,任意の半径rの周速度vθは,式(1)のように表せます。

これより,渦管円周の半径aにおける循環Γを考えると,式(2)のように表せます。

これが,強制渦の周速度と循環です。式を見ると,角速度ωと半径r(渦管円周の半径r)に比例関係となります。つまり,半径が大きくなるほど,角速度が大きくなるほど,周速度および循環が大きくなります。これが巨大なものであれば,凄まじい破壊力を持った渦になることが容易に想像できます。
(4)渦管外で流体が渦管の影響を受けて円運動をする,半径rにおける円周に沿って循環している渦(自由渦)
次に,自由渦の解説をしていきます。自由渦は,流体微小要素が渦管の影響によって,円運動もしくは半径rにおける円周に沿って循環している渦を示します。これは,図3のような速度分布となります。
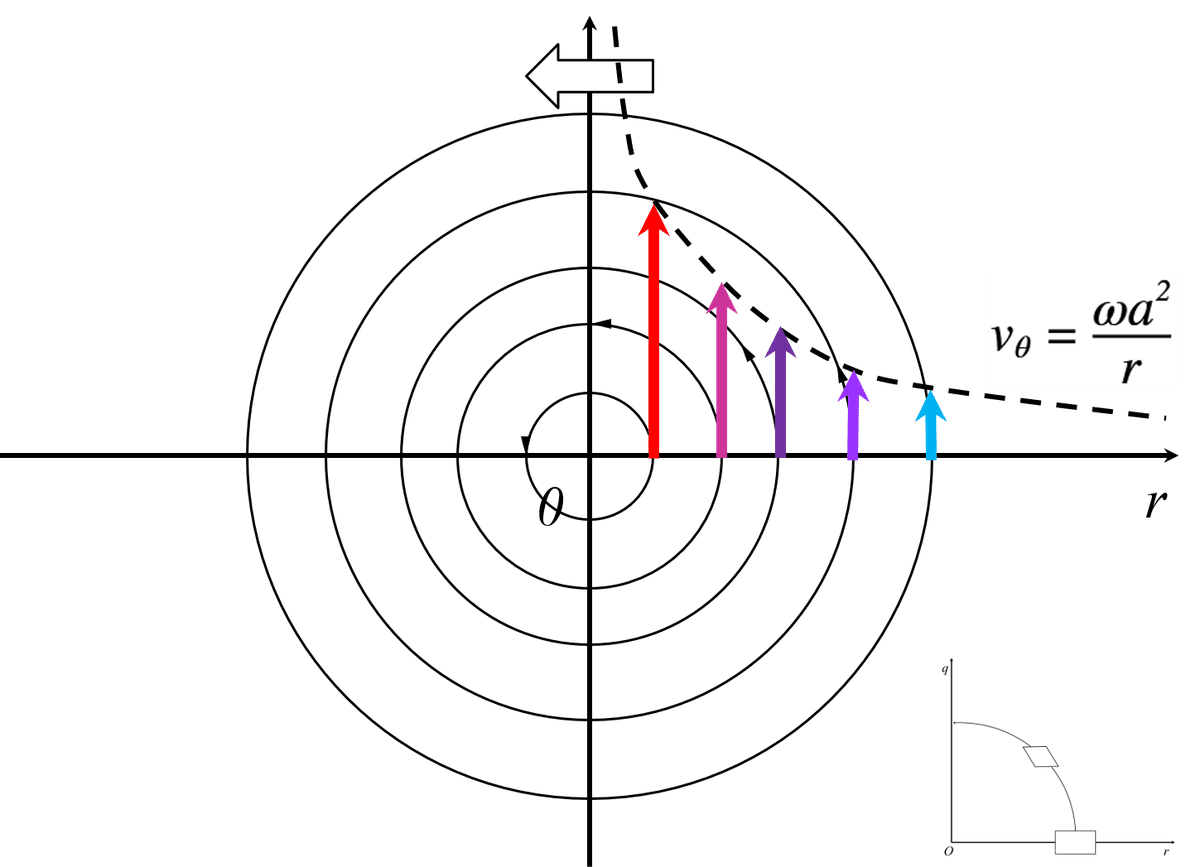
図3 自由渦の速度分布
強制渦とは逆に,円周に沿う循環Γから求めると,任意の半径rの周速度vθは,式(3)のように表せます。
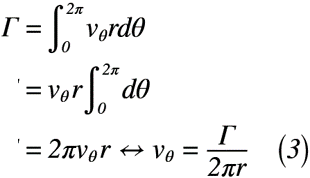
ここで,循環Γが強制渦で求めた式(2)と仮に同様の値をとると考えると,周速度vθは,式(4)のように表せます。(このように循環が同様な結果となることは,実は成立することが分かっているので,正しい仮定となります。詳しくは,「渦に関する法則(その2)」を参照してください。)

これにより,式(4)の結果から渦度ζを円筒座標系のナビエ・ストークス方程式(N-S方程式)を用いると,式(5)のように表せます。(ちなみに2次元流れ,定常流れかつ密度が一定となる非圧縮性流体であると仮定してます。)

式(5)の結果から,渦度はゼロとなるので「渦無し流れ」となるので,「自由渦」となります。
式(1)及び式(2)の結果から,渦管の内側では,流体は円運動及び循環していることが分かりました。一方で,式(3)及び式(4)の結果から,渦管の外側では,流体は円運動をしていますが,式(5)の結果から,渦運動はしていないポテンシャル流れであることが分かりました。
(5)まとめ
今回の記事のまとめを以下に示します。
(1)渦周りのポテンシャル流れは,2次元流れ中の任意のある1点を中心として,半径aの渦管と循環Γがある場合の流れを想定している。
(2)強制渦の周速度と循環は,角速度ωと半径rに比例関係となる。
(3)自由渦の循環は,周速度vθと半径rに比例関係となる。
以上です。最後まで閲覧頂きありがとうございました。
※次回は,「渦周りのポテンシャル流れ(その2)」を取り扱う予定です。
いいなと思ったら応援しよう!

