
流体力学 翼理論
最近,流体力学を再度学び直してみようと思い,記事にしています。
第56回目は,「翼理論」について紹介したいと思います。今回は,主に翼断面(他の断面に共通で使える断面)に加わる力について取り上げます。
(1)物体に働く力
さて,今回は翼断面(他の断面に共通で使える断面)に働く力を紹介します。条件は,2次元の物体が流速Uで流れている流体中に置かれているとき,もしくは,物体が静止流体中を流速Uで動いているときを想定します。図1に物体に作用する力,抗力,揚力の概念図を示します。
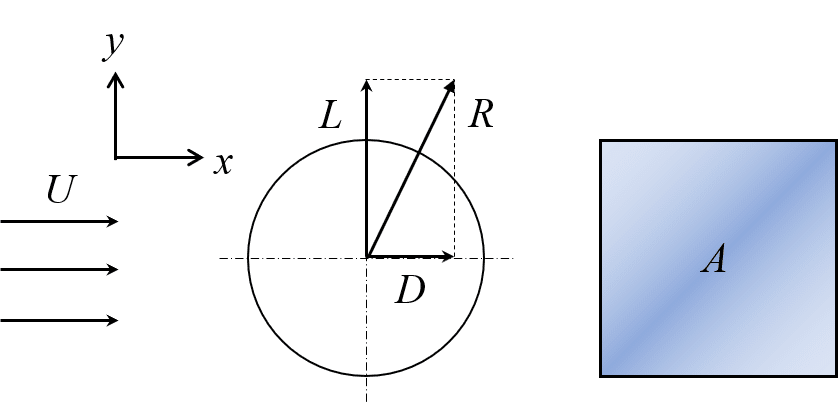
ここで,R:物体に作用する力,D:流れに平行なx軸方向成分の力(抗力),L:流れに垂直なy軸方向成分の力(揚力)を示します。
何となく聞いたことがあると思いますが,抗力は英語でDrag(ドラッグ)といいます。もはや英語が日本語化してきていると筆者は思います。特に,モータースポーツの最高峰F1では,よくマシンの空力特性がドラッキー(=抵抗の大きいマシン)なのかをよく議論しております。
また,揚力は英語でLift(リフト)といいます。これも英語が日本語化してきている用語の1つではないでしょうか。飛行機では,空を飛ぶのにこの力が必須です。但し,ただ単に揚力やリフトと言わず,方向成分を追加した「アップリフト」ということが多いのではないでしょうか。(あくまでの筆者の感想です)
一方で,F1は飛行機の翼形断面を上下反転させたものを利用しております。これは「ダウンリフト」とはいわず,「ダウンフォース」とよく呼びます。(恐らく,最初に言った人の慣習に習ったものではないでしょうか)
では,物体に作用する力を抗力と揚力に分解できたわけですが,抗力Dと揚力Lは式(1)のように記述できます。但し,式(1)はニュートンの第2法則(運動方程式)と同様で,経験則に基づく立式だと考えています。

ここで,ρ;流体密度,U:一様流れの速度,Cd:抗力係数,Cl:揚力係数,A:代表面積を示します。
抗力係数Cdと揚力係数Clは,物体形状やレイノルズ数(流れ場が層流か乱流を判断する無次元量)等に依存する無次元量です。つまり,値が状況により変化するということです。
代表面積Aは,x軸に垂直な面に物体を投影したときの面積,もしくは,流れ方向に依存しない面積を使います。図1では,「x軸に垂直な面に物体を投影したときの面積」を使うことになります。
図1では,適当な物体形状でお話ししましたが,翼形でも同様の議論ができます。条件は,断面一定となる翼幅が無限に長い2次元翼に働く力を想定します。図2に翼形に作用する力,抗力,揚力を示し,抗力Dと揚力Lは式(2)のように記述できます。
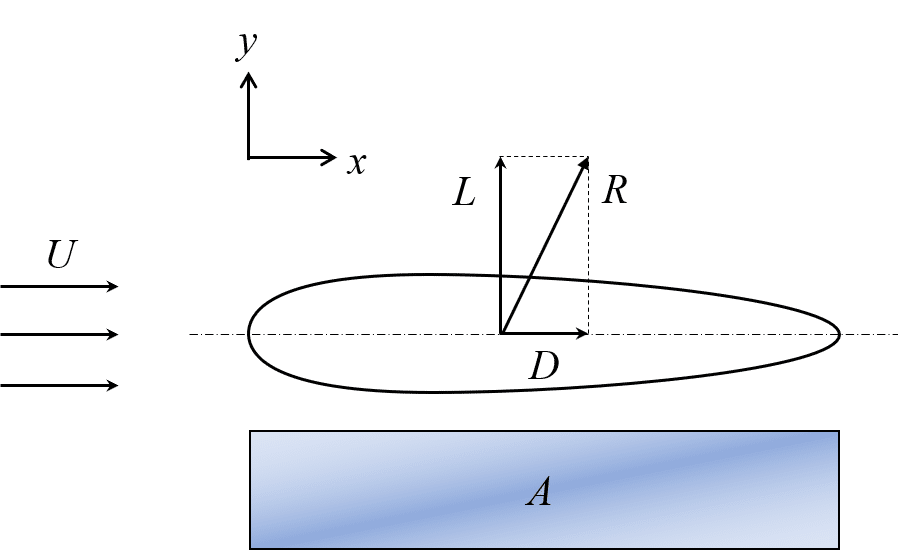
ここで注意してほしいのは,代表面積Aのことです。先ほどの図1では,「x軸に垂直な面に物体を投影したときの面積」を使いましたが,今回の図2では,「流れ方向に依存しない面積」を使うことになり,使う断面積が変わるのです。また,2次元翼の場合は,単位翼幅当たりの翼断面積を基準面積とするケースが多く,幅bを1mとして考えるため,式(2)のような記述になっております。
つまり,式(1)の単位は「N(ニュートン)」でしたが,式(2)の単位は「N/m(ニュートン毎メートル)」ということになります。

(2)抗力について
では,流れに平行なx軸方向成分である抗力についてもう少し掘り下げていきます。抗力もかなりの種類が図3のように分類されると考えられています。

まずは,「翼の抗力における断面抗力」を取り上げます。この断面抗力を考えるために,図4のような2次元物体の微小面積に働く抗力を考えます。

図4の解説をします。流れ場は物体と平行に流れる一様流れを想定します。このとき,物体にはよどみ点(流速がゼロとなる点) ができ,このよどみ点から時計回りの方向に角度θを取ります。
このときの微小面積dAに働く力は,流れの方向を考えると,pdAcosθとなります。そして,この力を求めるには表面積全体で積分すればよいので,式(3)のようになります。
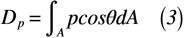
この力は圧力pによる抵抗なので,「圧力抵抗」と呼ばれ,「翼の抗力における断面抗力」の1つです。
同様に,別の断面抗力を考えるため,図5のような2次元物体の微小面積に働く抗力を考えます。

図5の解説をします。流体は本来ニュートンの粘性法則から「粘度」を想定します。(これまでの理想流体では,この粘性を考慮していませんが,今回に限り考慮します)
このとき,物体の表面に沿って,流体の粘性による壁面せん断応力が曲線の接線方向に働きます。このときの微小面積dAに働く力は,せん断応力の流れの方向を考えると,τdAsinθとなります。そして,この力を求めるには表面積全体で積分すればよいので,式(4)のようになります。

この力は壁面せん断応力τによる抵抗なので,「摩擦抵抗」と呼ばれ,「翼の抗力における断面抗力」の1つです。
この2つの力が断面抗力となるため,以下のように表せます。

次に,「翼の抗力で翼端の存在による誘導抗力」を取り上げます。図6に誘導抗力の概念図を示します。
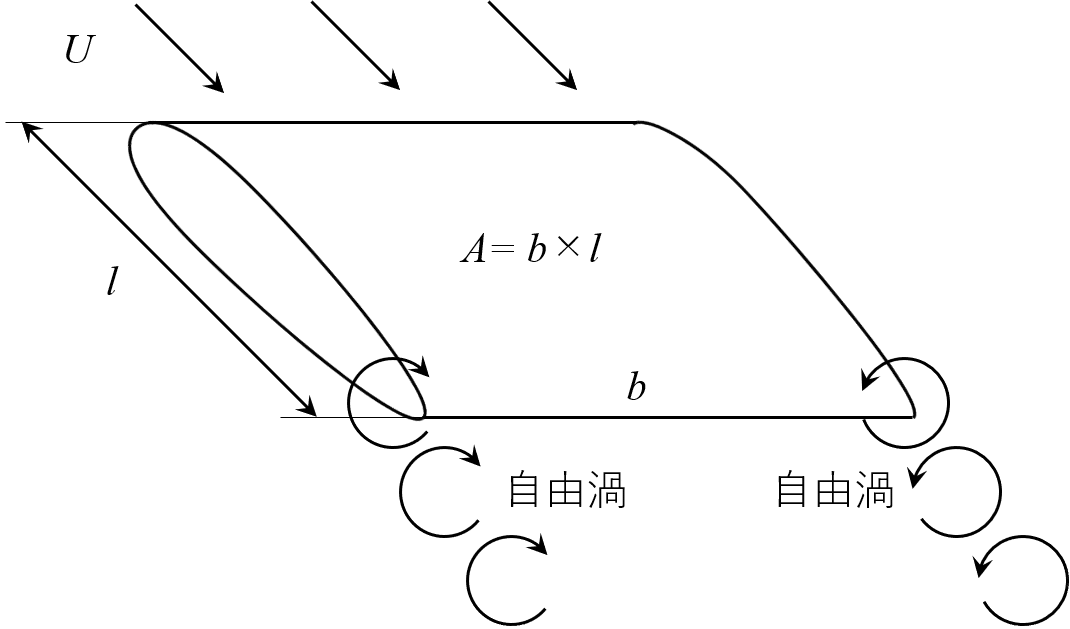
これは,モデル想定で考えている2次元翼ではなく,実際の3次元翼を考えるときに発生する力です。つまり,「誘導抗力」は「3次元形状物体の両端から放出される縦渦による抗力」です。誘導抗力を立式すると,抗力の式(1)と同様に,式(5)のようになります。

ここで,Cdiは誘導抗力係数を示します。
このように,「誘導抗力」は「3次元形状物体の両端から放出される縦渦による抗力」と説明できます。
結論からいえば,縦渦が問題になるのは「翼端」です。なせならば,端部に発生した縦渦は翼の下面から上面に空気が巻き込まれることで,翼の上面・下面でつり合いの取れていた空気流が乱れてしまい,翼端後方に渦ができてします。翼の中央と端部で2次元翼を考えると,端部の空気流の流れが乱れることで渦以外にも,揚力の向きが真上から少しズレるなどの問題が生じます。
そのため,実用上のお話しをすると,飛行機の翼端は必ず「ウィングレット」というものが取り付けられます。これは,前述した「誘導抗力」を小さくする,すなわち,縦渦を抑制するものです。図7にウィングレットと縦渦の関係を示します。
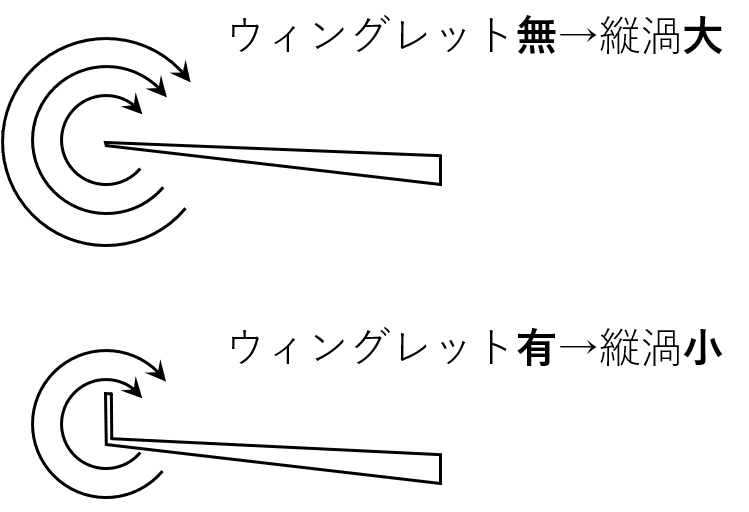
モータースポーツの世界でも「GTウィング」という言葉を車好きなら聞いたことがあるはずです。これも縦渦を抑制するために翼端形状は,ウィングレットと同様のものが取り付けられています。最近のF1のリアウィングでは少々わかりづらいので,日本国内レースの最高峰SuperGTのGT500車輛やWRC(世界ラリー選手権)のRally1車輛のリアウィングを見ると,わかるのではないでしょうか。
最後に,「翼以外の抗力である断面抗力」を取り上げます。例えば,飛行機を考えたときは,飛行機本体などにより発生する抗力のことを指します。今回は,どんな抗力があるのかを箇条書きに紹介します。
・造波抵抗:戦闘機が音速を超えたときに生じる衝撃波,船舶で生じる水面波による抗力
・干渉抵抗:複数物体の相互干渉(並列する橋梁など)による抗力
以上の抗力によって,全抗力は式(6)のように算出されます。但し,実際の設計ではこれらの抗力を全て求める訳ではなく,解析可能な範囲で求めるものを考えられます。
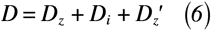
(3)揚力について
では,流れに平行なy軸方向成分である揚力についてもう少し掘り下げていきます。しかし,揚力は抗力とは異なって分類されるほど種類がなく,前述した抗力の「圧力抵抗」と「摩擦抵抗」の2つが揚力に切り替わったものがメインとなります。図8に2次元物体の微小面積に働く揚力を示します。
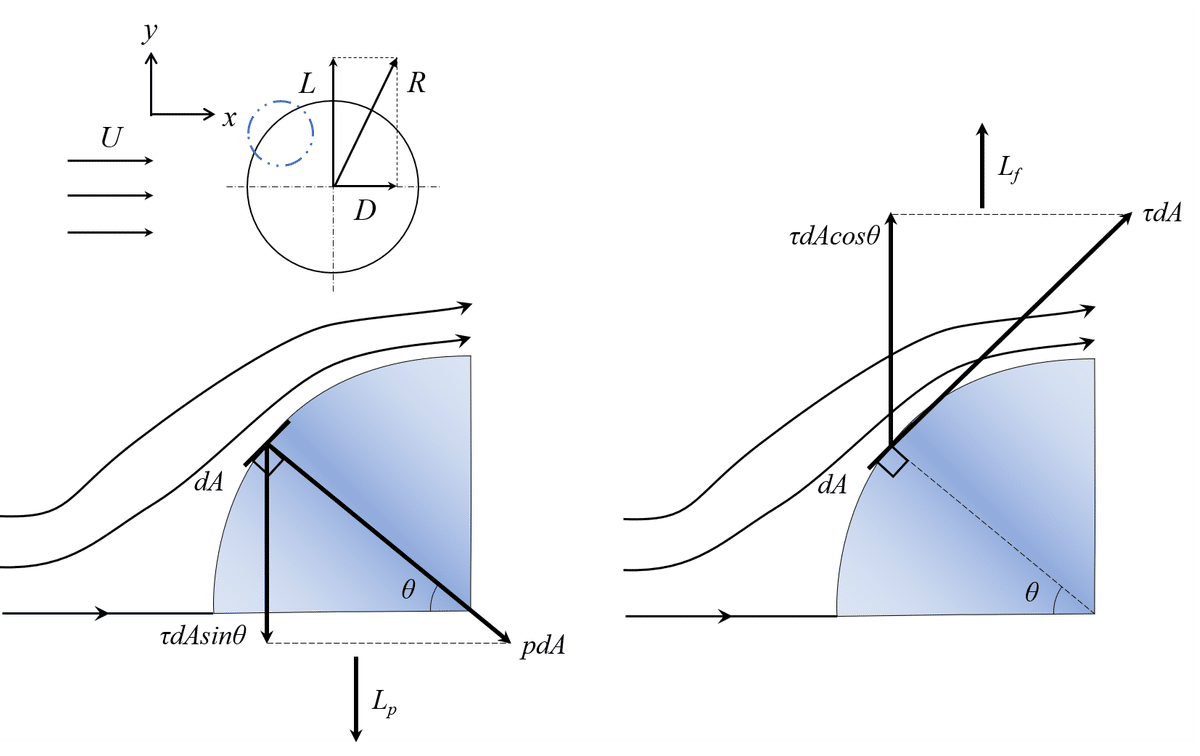
そのため, 圧力pによる揚力である「圧力揚力」と壁面せん断応力τによる揚力の「摩擦揚力」の2つが「翼の揚力における断面揚力」となり,式(7)のように記述できます。
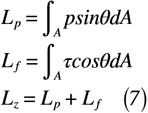
以上まとめたように,翼に働く力は抗力と揚力がどのように働いているかを基本としています。
(4)まとめ
今回の記事のまとめを以下に示します。
① 2次元の物体が流速Uで流れている流体中に置かれている場合,物体に作用する力を分解すると,抗力と揚力に分類できる。
② 抗力は,翼の抗力(断面抗力と誘導抗力)と翼以外の抗力で全抗力が求められる。
③ 揚力は,翼の揚力(断面揚力)のみで全揚力が求められる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「翼理論(その2)」について,解説する予定です。
いいなと思ったら応援しよう!

