流体力学　渦度の証明

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第３０回目は，第２９回目で予告した通り「渦度の証明」について紹介していきます。

（１）渦度の証明（直交座標と円筒座標）

　 「渦度」については，以前の記事を確認してみて下さい。

　そのとき，渦度を定量的に評価するために，直交座標系および円筒座標系の式を取り扱いました。今回は円筒座標系の数式の証明をついてメインに取り上げます。ちなみに，直交座標系の渦度の式については別の記事にて解説していますので，合わせて確認してみて下さい。

（２）渦度の式（事前準備パート１）

　まず，渦度のときの直交座標と円筒座標を図１に示します。

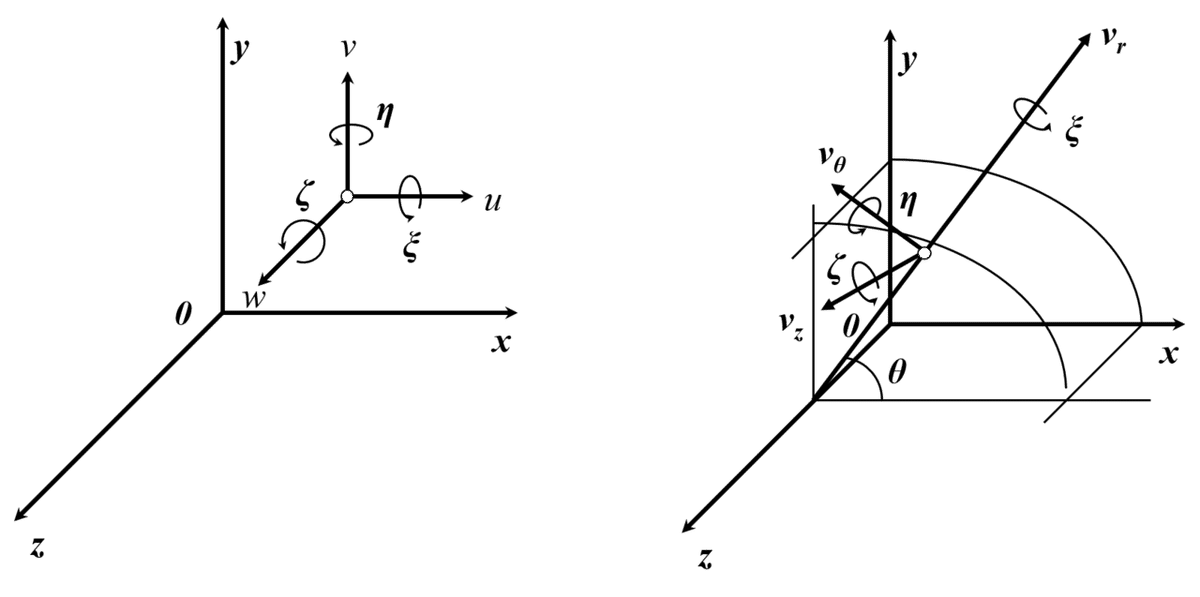
図１　直交座標と円筒座標

　ここで，何となく円筒座標系は「こんな感じなのかな？」という感覚で構いません。モデル化するうえで大事なのは，図２の円筒座標です。

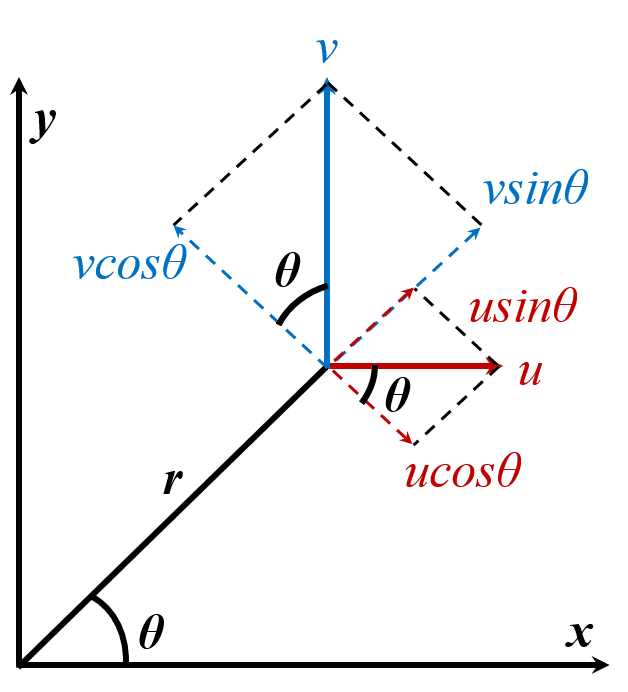
図２　円筒座標

　では，図２に沿って円筒座標の半径r方向，円周θ方向および高さz方向の速度を最終的に算出します。まず，上記の速度は，式（１）～式（３）のようにそれぞれ表せます。

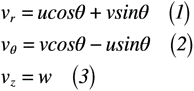
　ここで，x, y, z方向の速度u, v, wをそれぞれ求めると，式（４）～（６）のようにそれぞれ表せます。

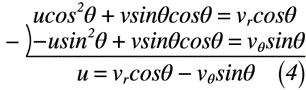
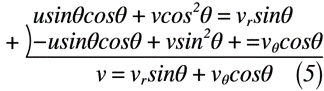
　また，必要となる知識として，三角関数の単位円の考え方を使います。そのため，使える形に変形したものは，式（７）のように表せます。

　さらに，r, θをx, yについて微分する際に必要となるtan（タンジェント）の加法定理，微分および逆関数の微分について示します。

【加法定理】

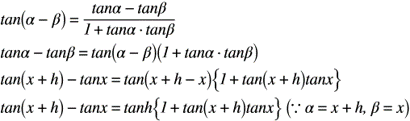
【微分】

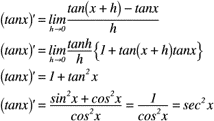
【逆関数の微分】

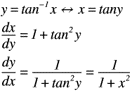
　上記の関係式を総動員してr, θをx, yについて微分すると，式（８）～式（１１）のように表せます。

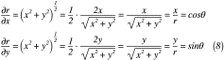
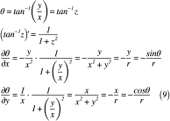
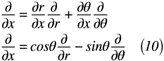
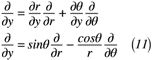
　これで，円筒座標系で使う数学の準備は終了ですが，まだ渦度に使える形にはなっていません。次項では，渦度に使える形の準備をしていきます。

（３）渦度の式（事前準備パート２）

　ここでは，前述した円筒座標系の証明を利用して渦度に使える形にしていきます。渦度では，x, y, z方向の速度u, v, wをそれぞれx, y zについて微分したものになっているので，速度を微分したものを式（１２）～式（１７）のようにそれぞれ表せます。

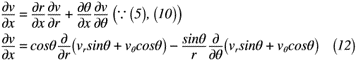
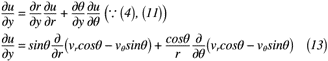
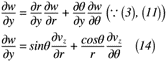
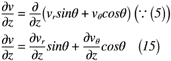
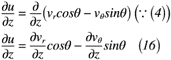
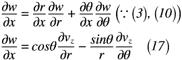
　これにて，ようやく準備が整いました。次項では，直交座標の渦度から円筒座標の渦度へ座標変換をしてみましょう。

（４）渦度の証明（直交座標→円筒座標の座標変換）

　ようやく，渦度の式を直交座標から円筒座標へ座標変換するところまでたどり着きました。まずはじめは，z軸方向を軸心とする渦度ζから証明していきます。証明の経過は，式（１８）のように表せます。

　次に，半径方向を軸心とする渦度ξを証明していきます。証明の経過は，式（１９）のように表せます。

　最後に，円周方向を軸心とする渦度ηを証明していきます。証明の経過は，式（２０）のように表せます。

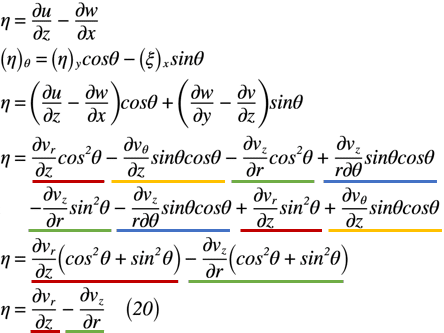
　よって，渦度の式は式（２１）のように表せます。

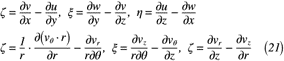
　ここで，上が直交座標，下が円筒座標の渦度の式をそれぞれ示しています。教科書に依りますが，ここまで証明を解説しているものあれば，座標変換だけをしただけの式を掲載しているだけのものあります。必要に迫られたときは，載っている教科書を参考にするなり，本記事を参考にしてもいいのではないでしょうか。

（５）まとめ

　今回の記事のまとめを以下に示します。
（１）渦度には，直交座標と円筒座標の２つの表し方が存在する。
（２）円筒座標の証明では，タンジェントの加法定理，微分および逆関数の微分が必要になる。
（３）渦度の証明は，丁寧に符合の違う同じ多項式を消去することが求められる。

　以上です。最後まで閲覧頂きありがとうございました。

　※次回は，循環について扱う予定です。
　※「任意の角度を回る流れのグラフ」については，別日に投稿しますので，少々お待ちください。

（６）おまけ

　筆者の高専時代は，古典力学で円筒座標系の証明を自力で証明したのですが，これ以降，物理の勉強をしばらくしなくなりました（笑）。それだけ労力がかかる箇所でもあり，「こんなのが続くのか」と思うと手が止まってしまうものです。そして，必要なことにも手がつかなくなることもあります（結果，この分野の試験は見事赤点でした）。
　式の証明は，モデル化の理解を含めて大事ですが，工学ではこれらの式は「合っているもの」として「利用する側」の立場をとります。よって，設計や製作の現場では計算ができればいいのです。このような証明は，できるに越したことはありませんが，計算ができることが最優先事項だと筆者は思っています。
　だからこそ，学生の方は，手が止まっているときほど，計算問題を解きましょう。こんな証明ができないくらいで，他のことにも影響を及ぼすようなものではありません。気にし過ぎないことです。
　社会人の方は，式の証明に囚われすぎると，手持ちの業務に支障をきたします。支障がない程度に式の証明とは向き合いましょう。