
流体力学 ブラジウスの第2公式
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第60回目として「ブラジウスの第2公式」について紹介したいと思います。前回の投稿で「ブラジウスの第1公式」とその有効性を記事にしておりますので,ご確認ください。
(1)ブラジウスの第2公式
では,ブラジウスの第2公式を導出してみましょう。ブラジウスの第1公式で使ったときと同様に,図1はz平面における任意断面を柱状体の概略図を示します。

このとき,流れが物体(柱状体)に働く全圧力x,y方向をそれぞれPx,Pyとし,流れが物体に働く圧力の座標原点に関するモーメントMは,式(1)のようになり,この式(1)こそ「ブラジウスの第2公式」なのです。
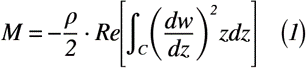
先ず,柱状体(単位長さ1とした2次元)の周辺の任意の1点より,図1のような三角形を考えます。このとき,ds;線素,dx:x方向成分の線素,dy:y方向成分の線素,α:任意の角度,pds:dsに対して垂直に働く流体の圧力による力を示します。
この線素dsに働く力pdsのx,y方向成分pdssinα,pdscosαからpdsの座標原点に関する微小モーメントdMは,式(2)のようになります。

ここで,三角関数の定義に立ち返ると,dsは式(3)のように考えることが出来ます。

得られた式(3)を式(2)へ代入すると,式(4)に書き換えられます。

このとき,柱状体(三角形)周辺に沿って流れる流速qsと置くと,ベルヌーイの定理(定常流れのとき,物体の前後で運動エネルギーと圧力エネルギーがエネルギー保存側によって成立する定理)は,式(5)のようになります。

式(5)を式(4)へ代入すると,式(6)のようになります。

式(6)の下線部で示した部分を書き換えます。書き換えには,複素数の四則演算を使います。複素数x+iyと微小な共役複素数dx-idyを使って展開すると,実部Re(Real part)と虚部Im(Imaginary part)に分解でき,式(7)のように表現できます。

では,式(7)の実部Reを式(6)の下線部に適用すると,式(8)のようになります。

式(8)の柱状体(三角形)周辺に沿って流れる流速qsに注目すると,流速qsは2乗されているため,x,y方向成分の速度をそれぞれu,vを使って表現し直します。具体的には,複素数と共役複素数形式で記述すると,式(9)のようになります。

式(9)を式(8)へ代入すると,式(10)のようになります。

式(10)の下線部は,微分記号があって気持ち悪いので,さらに書き換えます。以前の記事で取り上げた「流線の式」を使用します。式(11)に流線の式を示しますが,詳細が知りたい方は過去の記事をご確認ください。

今回は,式(10)の下線部に対応した多項式のみを流線の式(11)を使って,式変形したものを式(12)として示します。

ここで,式(12)を式(10)へ代入すると,式(13)のようになります。

式(13)に注目すると,右辺の積分は,柱状体周辺に沿っての1周積分です。この話は,過去の記事で取り上げた「コーシーの積分定理」が使えます。詳細は,過去の記事をご確認ください。
式(13)に注目すると,コーシーの積分定理によって,柱状体周辺を囲む任意の閉曲線Cの間に(dw/dz)^2の特異点(正則でない点,すなわち微分不可能な点)がない場合は,柱状体周りの長さsに沿う積分を任意の閉曲線Cに沿う積分に置き換えが出来ます(過去記事の「2重連結領域」に該当する)。
以上の話を用いて,式(13)の1周積分の場所を置換すると,式(14)のようになります。

式(14)は,式(1)と同様の式になったことから「ブラジウスの第2公式」が導出できました。ここで,w:柱状体周りの流れの複素ポテンシャル,ρ:流体密度,C:柱状体を囲む任意の閉曲線,Re[]:実数部を示します。
ここまでの証明で分かった通り,ブラジウスの第1公式も,第2公式の証明も同様に,ベルヌーイの定理とコーシーの積分定理を利用することで証明ができます。
(2)まとめ
今回の記事のまとめを以下に示します。
① ブラジウスの第2公式は,物体に働く「モーメント」を求めるものであり,ベルヌーイの定理とコーシーの積分定理を用いて導かれる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「ダランベールのパラドックスとクッタ・ジューコフスキーの定理」について取り上げます。
いいなと思ったら応援しよう!

