
流体力学 等角写像(例題編)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第48回目は,「等角写像」について紹介していきます。なお,等角写像は理論編と例題編として連載記事となっておりますので,以前の記事もご覧ください。
(1)等角写像(その1)
まず,「等角写像」の1つ目の例題に触れましょう。
【例題1】
z平面において原点を中心とする半径aの円を次に示す関数(式(1))によって,ζ平面に写像すること。
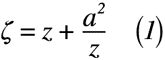

z平面は,複素数の極座標系を考えるために円周上の任意の点を式(2)で表します。

よって,式(2)を式(1)へ代入すると,式(3)が得られます。

したがって,z平面からζ平面に写像した結果が式(3)となるわけです。別の平面に写像した与式は何も関係なさそうですが,実はそうではないのです。もし,z平面がθ=0,πの場合,ζ平面ではξ=2a,-2aでかつη=0となります。つまり,z平面でz点が円周をθ=0~2πまで1周すると,ζ平面ではξ=2a~-2aまでを端として線分を1周することになります(図1)。
(2)等角写像(その2)
次に,「等角写像」の2つ目の例題に触れましょう。
【例題2】
z平面においてy軸上の点M(y=f)を中心とし,x軸上でx=±aを通る円は,次に示す関数(式(4))によってζ平面に写像すること。


ここで例題1の結果を思い出すと,z平面で半径aの円は,ζ平面で長さ4aの直線に写像されます。この考え方を利用すると,例題2はz平面で(x軸上)x=±aの点は,ζ平面でζ=±2aに対応します。よって,z平面の円周上の点zをζ平面に写像した点をζとしたとき,式(5)のように考えることとします。

ここでz平面のzと±aを結ぶ線分をそれぞれr1,r2とし,x軸とのなす角をθ1,θ2とします。また,ζ平面もζと±2aを結ぶ線分をそれぞれR1,R2とし,ζ軸とのなす角をΘ1,Θ2とすると,式(6)および式(7)のように記述できます。

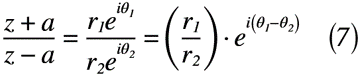
したがって,式(6)と式(7)の結果を等式として考えると,式(8)のように記述できます。

この結果から,z平面で点zが円を1周すると,対応する点ζはζ平面でζ=±2aを通り,Θ1-Θ2=-2θとなる円弧として1周します。なお,z平面の円(点z)とy軸(+側)との交点はζ平面の円(点ζ)とη軸(+側)との交点に対応するため(図2参照),ζ円弧のそりの高さを求めると,式(9)のように表せます。

ちなみに赤色の下線部については,変換が難しい部分であるために展開した結果を以下に示します。
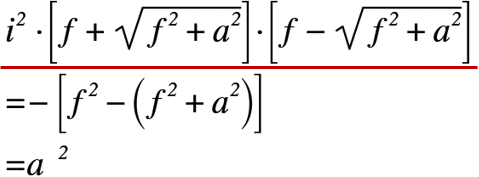
(3)等角写像(その3)
最後に,「等角写像」の3つ目の例題に触れましょう。
【例題3】
z平面において原点近くの点M(x,yいずれの軸上にもない)を中心とする円は,次に示す関数によってζ平面に写像すること。但し,円とx軸の正の部分はx=aで交わるとする。

z平面の円周上に点zと,Ozとx軸とのなす角θに等しくなるようにx軸に対してOzと反対側にOz’を引くと(図3参照),式(10)のように表せます。

よって,z’を考えると式(11)のように表せます。

これにより,z平面に対応するζ平面の式は式(12)のように表せます。

結果として,OzとOz’との合ベクトルOPを示す点Pは点zも対応する点ζで翼形に形成する点となります。
そして,このζ平面の写像に使う式(12)(式(1)や式(4)も同様)は,「ジューコフスキー変換」といい,図3に示したような翼形を「ジューコフスキー翼」と呼びます。そして,勘のいい方は何となく察していると思いますが,円の中心Mの位置によってジューコフスキー翼は様々な形が得られるそうです。
次回は,このジューコフスキー変換と翼をもう少し深堀りしていきましょう。
(4)まとめ
今回の記事のまとめを以下に示します。
(1)z平面で原点を中心とする半径aの円を変換すると,ζ平面で長さ4aの直線に写像する。
(2)z平面でy軸上の点Mとする半径aの円を変換すると,ζ平面で円弧(そりの高さζ0=2f)に写像する。
(3)z平面で原点近くの点M(x,yいずれの軸上にもない)を中心とする半径aの円を変換すると,ζ平面でジューコフスキー翼に写像する。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「ジューコフスキー変換・翼」について,解説する予定です。
いいなと思ったら応援しよう!

