流体力学　自由渦の2次元流れ

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第１４回目は，第１３回目で予告した通り，「渦」について紹介していきます。

（１）渦の2次元流れについて

　さて，わき出しと吸込みと同様に「渦」の２次元ポテンシャル流れを記述するには，ポテンシャル流れと流れ関数を含む複素関数，コーシー・リーマンの微分方程式が必須となります。詳しくは，以前の記事を確認してみてください。

　今回は詳しく解説はしませんが，渦の流れの様子を数学的に記述するには知っておくべき前提が2点ほど必要です。

　1つ目は，「渦」はわき出しと吸込みと同様に「円運動」をしていること，すなわち半径方向，円周方向の分速度vr，vθを使って議論できることです。そのためには，2次元流れの直交座標から極座標へ切り替える必要があります。直交座標と極座標の関係は，単位円を考えると式（１）のように表せます。

　但し，極座標に切り替えるとはいっても，直交座標にかくための必要な準備です。2次元流れの極座標（r,θ）に必ず出てくるのは，原点から任意の点までの距離（半径r）とx軸とのなす角θの2つです。半径rとx軸とのなす角θは，式（２）のように表せます。

　よって，式（２）を使えば，直交座標に今まで通り，2次元流れの様子をかくことができます。

　2つ目は，循環の定義によって円周方向の分速度vθが決まることです。今回も循環については，詳しくは触れないことにしますが，循環Γが一定値，すなわち値が変化しないものと考えると，以前の記事で取り扱った「渦無し流れ」となり，「渦度」が零となります。よって，今回取り扱う渦は「自由渦」であり，循環の定義式から円周方向の分速度vθは半径ｒに反比例する関係となるので，円周を通る循環の定義式は，式（３）のように表せます。

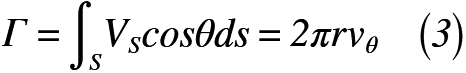
　よって，式（３）から半径方向分速度vr，は「自由渦」の場合，存在しないこともわかります。これで，渦はもとい「自由渦」の下準備が整いました。次は，式（３）を使って，速度ポテンシャル，流れ関数と複素速度ポテンシャルをそれぞれ考えてみましょう。

（２）自由渦の場合

（２-１）速度ポテンシャル

　では，式（３）で表した半径方向，円周方向の分速度vr，vθから速度ポテンシャルを表していきます。まず，半径方向，円周方向の分速度vr，vθは極座標形式のコーシー・リーマンの微分方程式でかけるため，式（４）のように表せます。

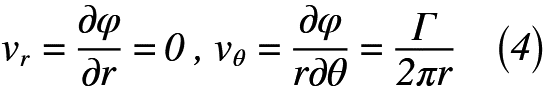
　式（４）をそれぞれr，θについて微分すると，式（５）のように表せます。

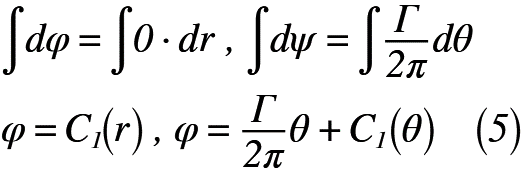
　ここで，Ｃ1(r)，C1(θ)はそれぞれr, θの関数とします。また，式（５）はいわゆる微分方程式の一般解であることから，これを特殊解とする必要があります。そのために，境界条件を与えます，θ=0の場合，φ=0とすると，式（５）を満足するφの式（６）へ書き直せます。

　よって，式（６）が自由渦の速度ポテンシャルとなります。

（２-２）流れ関数

　では，式（３）で表した半径方向，円周方向の分速度vr，vθから流れ関数を表していきます。まず，半径方向，円周方向の分速度vr，vθは極座標形式のコーシー・リーマンの微分方程式でかけるため，式（７）のように表せます。

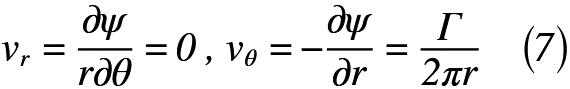
　式（７）をそれぞれr，θについて微分すると，式（８）のように表せます。

　ここで，C2(θ)，C2(r)はそれぞれθ, rの関数とします。また，式（８）はいわゆる微分方程式の一般解であることから，これを特殊解とする必要があります。そのために境界条件を与えます，r=1の場合，ψ=0とすると，式（８）を満足するφの式（９）へ書き直せます。

　よって，式（９）が自由渦の流れ関数となります。

（２-３）複素速度ポテンシャル

　では，自由渦の速度ポテンシャル【式（６）】と流れ関数【式（９）】を使うと，式（１０）のように表せます。

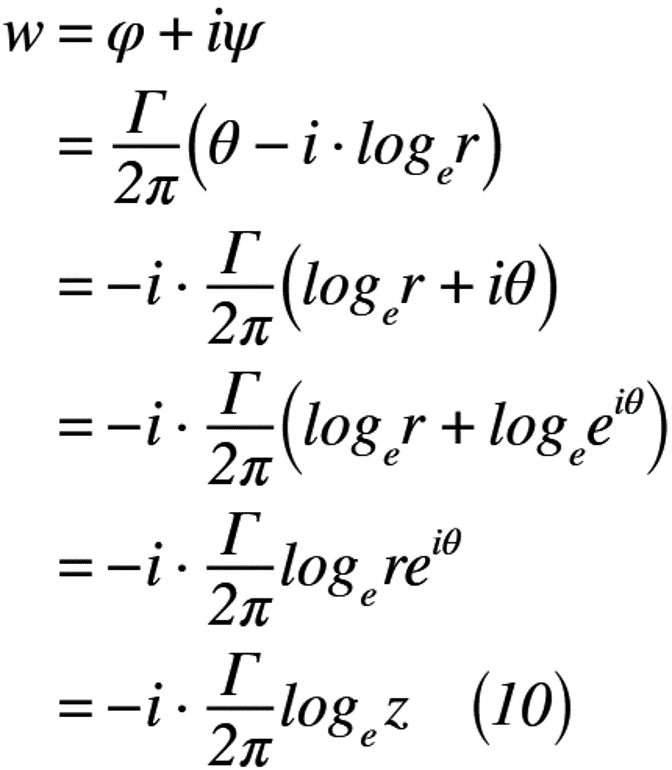
　よって，式（１０）が自由渦の複素ポテンシャルとなります。ここで，式（６），式（９）や式（１０）にある循環Γは，「渦の強さ」と呼ぶことがあります。結局のところ，循環Γが大きくなると，円周方向の分速度vθが大きくなる比例関係があるため，このように呼ぶ習慣になったのではないかと筆者は思っております。

　また，式（１０）から自由渦の流れの状態が分かります。

　まず，式（１０）の速度ポテンシャルφ=const.（一定値）は，x軸とのなす角θ=const.（一定値）と考えることができるため，放射状の等ポテンシャル線が描けます。次に，流れ関数ψ=const.（一定値）は，半径r=const.（一定値）と考えることができるため，原点を中心にとする同心円状の流線が描けます。
　ここで，等ポテンシャル線を点線，流線を実線として書いたグラフを図１に示します。

図１　自由渦の2次元流れ

　よって，自由渦の2次元流れは，わき出しの2次元流れと比較して，等ポテンシャル線と流線が入れ替わったのみで，自由渦の中心を特に「渦点」と呼びます。

（３）まとめ

今回の記事のまとめを以下に示します。
（１）渦の2次元流れは，主に「自由渦」である。
（２）循環の定義より円周方向の分速度から速度ポテンシャルと流れ関数を求めることができる。
（３）「自由渦」は，「わき出しと吸込み」の2次元流れグラフを比較すると，等ポテンシャル線と流線が入れ替わったのみである。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，自由渦のグラフを扱う予定です。

改訂1（2022/03/07）
（2）自由渦の場合
（2-3）複素速度ポテンシャル
×「等ポテンシャル線を実線，流線を点線」
〇「等ポテンシャル線を点線，流線を実線」