流体力学　薄翼の理論

　皆様おはこんばんちは。
　最近，流体力学を再度学び直してみようと思い，記事にしています。
　今回は，第65回目として「薄翼の理論」について紹介します。尚，補足編の「薄翼理論の数学」で薄翼理論を勉強するためだけに必要な数学を取り上げております。

（1）薄翼の影響因子

　はじめに，薄翼の理論と題していますが，薄翼に影響を及ぼす影響因子を以下に4つ紹介します（式（1）～（4）参照）。

この4つの影響因子（揚力L，揚力係数CL，前縁周りのモーメントM，モーメント係数CM）を急に紹介されてもよくわからないと思いますので，本記事ではこの4式を1つずつ証明していきます。（本記事は，揚力L，揚力係数CLの2つを証明します）その準備として，証明するために必要となる「2次元翼モデル」からあらゆる仮定を求めておきます。

 

（2）2次元翼モデル

　まずは，2次元翼モデルを考えます。モデルの仮定におけるポイントは，「翼上面と下面で流速が異なること」です。流速と渦の層は流れの中に速度の不連続な面としてモデル化でき，「イコール」として考えられます（渦の層と渦列の（1）参照）。

この考え方を使い，図1のようにグラフも「翼形」ではなく，「翼形の平行線に沿った渦の層」があるように設定します。ここで，x軸は翼弦長方向，ｙ軸は任意の点ｘにおける翼の位置を示しています。

図1　2次元翼モデルの概略図
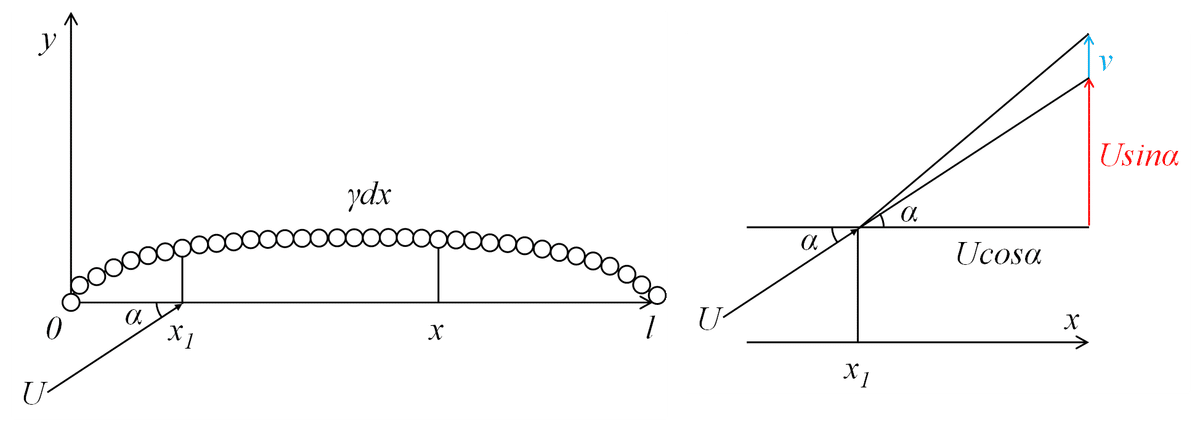
（左図：翼形の平行線に沿った渦の層，右図：一様流れの速度Uと迎え角αの拡大図）

翼形の中心線の微小部分dxの循環Γは，翼弦長l全体の循環と考えられるため，式（5）のように表せます（渦の層と渦列の式（2）参照）。

ここで，γdxの（強制）渦の層により任意の点x1でy方向に誘導される周速度は，式（6）のように表せます（渦周りのポテンシャル流れ（その1）の式（3）参照）。

よって，渦全体で任意のx1点に誘導される速度vは，翼弦長0～lまでの長さで積分すると，式（7）のように表せます。

渦全体で任意のx1点に誘導される速度vの関係式を見ていきましょう。翼に当たる一様流れの速度U，迎え角α，一様流れの速度Uと渦全体で任意のx1点に誘導される速度vの合速度，任意の点x1における翼の位置y，翼の傾きdy/dxと置きます。この関係は，図１に示すように翼面に接していることが必須条件，かつ迎え角αが限りなく小さいとすると，翼の傾きdy/dxは，式（8）のように表せます。

さて，以前に取り上げたジューコフスキーの仮定を考えてみます。（翼理論（その4）の1項参照）

この仮定では，とある翼の長さを与えると，全体の循環Γは求められますが，渦の層の強さγはなくなります。これは，翼の上面と下面で速度差により渦が発生しますが，翼の周りに循環Γが生じる一方で，翼の前端と後端には速度の淀み点が発生する所で「渦」が別途発生するというジューコフスキーの仮定を考えたために渦の層の強さγは「ゼロ」となります。そのため，2次元翼モデルでジューコフスキーの仮定を適用すると，x=l（翼弦長）のとき，γ=0となる境界条件が得られ，xとθの関数を考えると，式（9）のように表せます。（図1のグラフの外観に式を合わせたような恰好になります。）

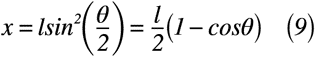
また，渦分布γもxとθの関数で表すと，式（10）にようにフーリエ級数を使った仮定をします。

但し，A0，Anは未知の定数（フーリエ級数）として最後に決定します。

 

（3）揚力Lの証明

　では，薄翼理論の揚力Lを導出してみましょう。揚力Lは，以前取り上げたクッタ・ジューコフスキーの定理（クッタ・ジューコフスキーの定理の式（1），（7）参照）を使用していきますが，その前の準備をここでしておきましょう。

まずは，ジューコフスキーの仮定を適用したxとθの関数（式（5））からです。最終的に揚力Lは渦分布を積分することで導出するので，式（9）をxについて微分すると，式（11）のようになります。

次に，クッタ・ジューコフスキーの定理を使用して導出してみます。ここで注意するべきは，積分するときにxの範囲からθの範囲に切り替えるため，定積分の範囲が変わることでしょうか。クッタ・ジューコフスキーの定理にジューコフスキーの仮定，渦分布を代入し，途中で加法定理を適用すると，式（12）となり，式（1）で示した薄翼理論の揚力Lと同様になります。

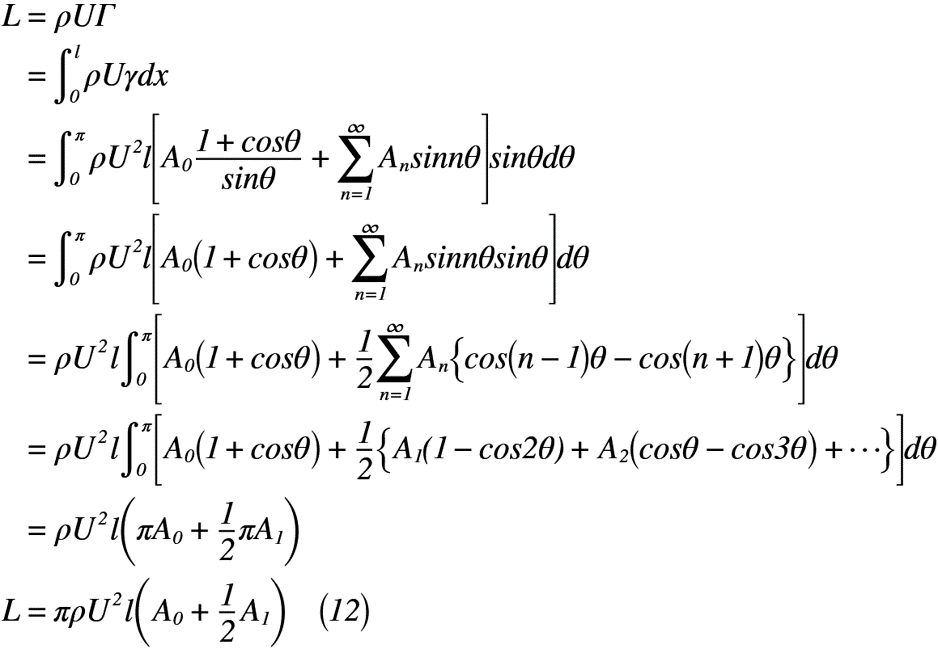
（4）揚力係数CLの証明

　次に，薄翼理論の揚力係数CLを導出してみましょう。揚力係数CLは，以前取り上げた揚力Ｌの定義式（翼理論の式（1）参照）を使用していきます。

 先ほど導出した薄翼理論の揚力L（式（12））と定義式は同じ揚力Lなので，お互いに同値と見なせます。以下のように計算すると，式（13）のようになり，式（2）で示した薄翼理論の揚力係数CLと同様になります。

（5）まとめ

今回の記事のまとめを以下に示します。
① 　薄翼理論の揚力Lは，クッタ・ジューコフスキーの定理からフーリエ級数で表した渦分布，ジューコフスキーの仮定を使うことで導出できる。
② 　薄翼理論の揚力係数CLは，薄翼理論の揚力Lと揚力Ｌの定義式が同じであることを使うことで導出できる。

 以上です。最後まで閲覧頂きありがとうございました。
次回は，「薄翼の理論（その2）」を取り上げる予定です。