
流体力学 円柱周りの複素ポテンシャル
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第50回目は,「ジューコフスキー変換・翼(その2)」を投稿しようとしていましたが,思ったより難航したため欠番にします。そこで,第51回目として「円柱周りの複素ポテンシャル」を投稿します。この記事は,等角写像の理論編やコーシー・リーマンの微分方程式を基に進めますので,以前の記事もご覧ください。
(1)円柱周りに何で流れが描けるの?
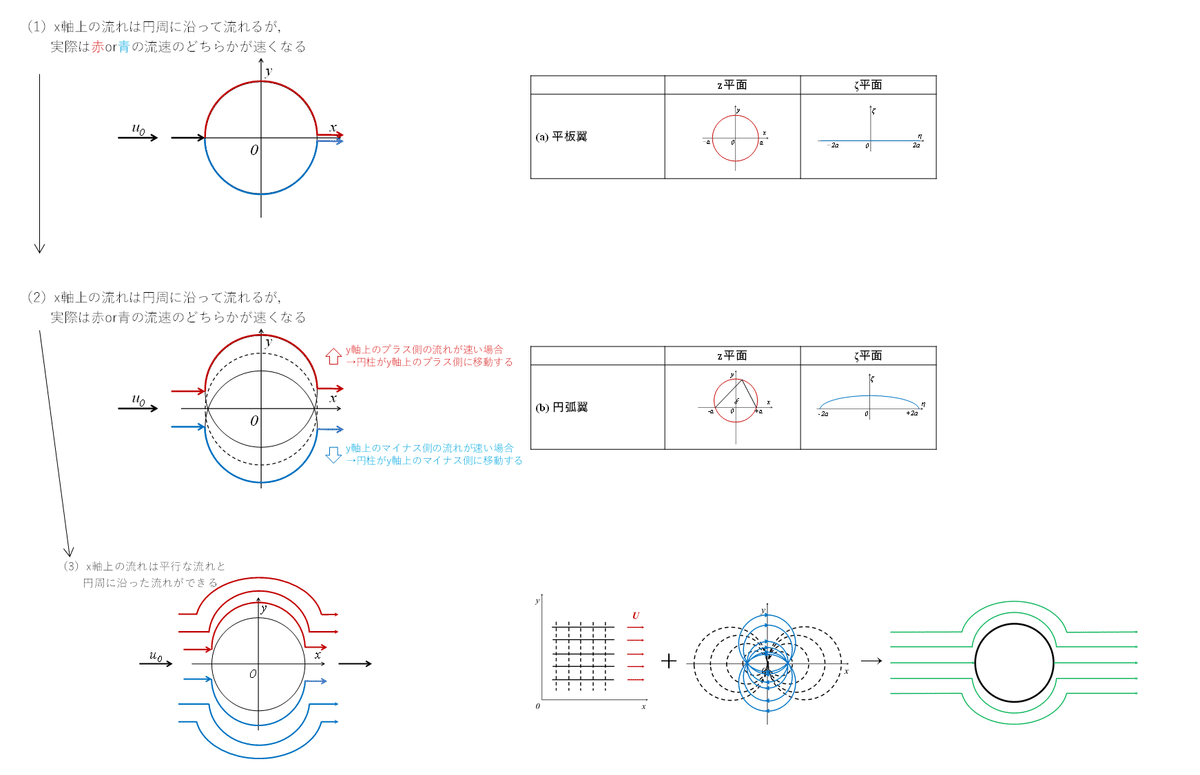
これまでの等角写像やジューコフスキーの変換の記事で伝えたかったことは,xy平面上に描いた形状をζη平面にジューコフスキー変換の式(1)を使うことで新たな形状に変化出来ることでした。表1に各翼型のz平面とζ平面の関係を示します。

とはいえ,なぜ円柱周りの複素ポテンシャルが描けるのでしょうか。表1をもう一度載せた理由がここにあります。
平板翼は,x軸上に流れる流速の流れに変換したものと考えます。ここで,円柱(平板翼のz平面)のx軸上を流れる流速のみを考えていますが,実際には円柱の円周に沿って流体が流れます。つまり,円周上を流れる流体は理論的に考えると,y軸上のプラス,マイナス方向で同じ量を流れる想定をしますが,実際の流体実験ではそうはいきません。必ずy軸上のどちらかに流速が多く流れます。よって,y軸上のどちらかに流速が多く流れる場合,円柱はy軸上のプラス,マイナスどちらかにズレるので,平板翼から円弧翼へ変化します。変化した円弧(円弧翼のz平面)のx軸上を流れる流速はζ平面上のようになると想像ができます。そうすると,円柱のx軸上は平行な流れが描けるのに対し,円柱から少しズレた位置の流れは,円周に沿うような流れとなり,円柱周りの複素ポテンシャルが描けたような感じになります。図1にこれまでの説明を示します。
このグラフを見て「ピン」と来た人はかなり流体力学を知っている人です。これは,過去にも記事に取り上げた「一様流れと2重わき出しの合成」に似ているではありませんか。
過去の記事でも,速度ポテンシャルと流れ関数までを導出していますが,今回は平板周りの複素ポテンシャル(一様流れと同様)からジューコフスキー変換を使った導出をしてみましょう。
(2)円柱周りの複素ポテンシャルについて
では,前項で取り上げた平板周りの複素ポテンシャルからジューコフスキー変換を使った導出をします。まずは,式(1)に平板周りの複素ポテンシャルを示します。ここでは便宜上,ジューコフスキー変換をする関係で複素数をzではなくζにしております。

次に,もう一人の主人公であるジューコフスキー変換の式(2)を示します。

ここで,式(2)を式(1)へ代入すると,式(3)が得られます。

少し道が逸れますが,式(3)を眺めてみましょう。式(3)は紛れもなく「一様流れと2重わき出しの合成の複素ポテンシャル式」です。
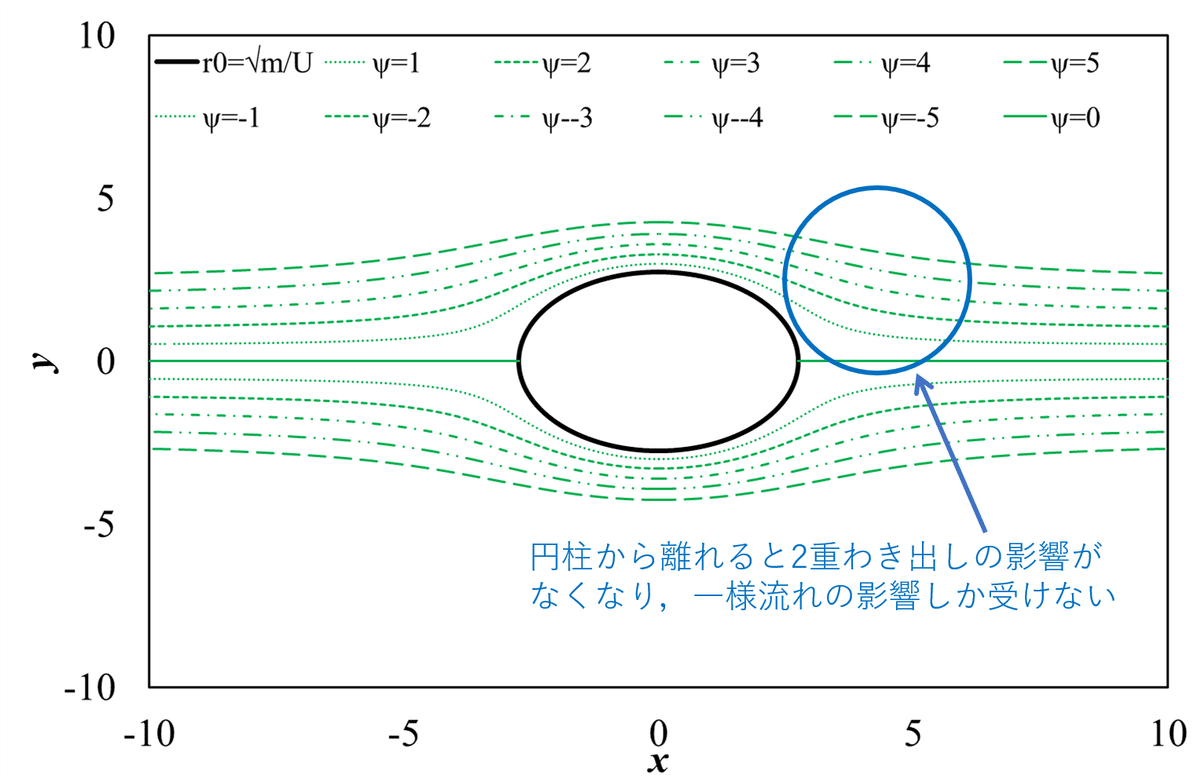
ここで,式(3)の右辺第2項は複素数zを無限大にすると,右辺第2項は「ゼロ」になります。この意味は,円柱が無限遠方にある流れは,2重わき出しの影響がなくなり一様流れだけになることです。
よって,グラフでは円柱から離れたところは,一様流れになっていることがこの式(3)で分かるのです。そんな当たり前なことをかくなと言われそうですが,グラフから読み取れることは,式でも同じことが言えないと整合がとなれないということです。図2に式(3)の考察結果を該当する流れ場を示します。
さて,ここで導出に戻ります。式(4)にオイラーの公式を使った複素数zを示します。

ここで,式(4)を式(3)へ代入して計算すると,式(5)が得られます。

この式(5)こそ,円柱周りの複素ポテンシャルです。式(5)から複素ポテンシャルと流れ関数をそれぞれ分けて記述すると,式(6),(7)が得られます。


ここで,式(7)の流れ関数を「ゼロ」として考えると,式(8)のようになり,θ=0又は,r=aとなり,式(5)は,速度u0の一様流れの中に,半径aの円柱が垂直におかれた場合の円柱周りの流れ場であることも確かめられました。
次項は,円柱周りの複素ポテンシャルが得られた後,計算によって算出できる流速と静圧について見てみましょう。
(3)円柱周りの流速と静圧について
では,円柱周りの流速と静圧について見てみましょう。まずは,流速からです。式(6),(7)の複素ポテンシャルと流れ関数をそれぞれ極形式のコーシー・リーマンの微分方程式を利用します。
計算としては,式(6),(7)をそれぞれ半径rと角度θで微分すると,半径方向の速度vrと円周方向のvθを算出でき,式(8),(9)が得られます。


ここで,図3に円柱周りの流れ場を示します。
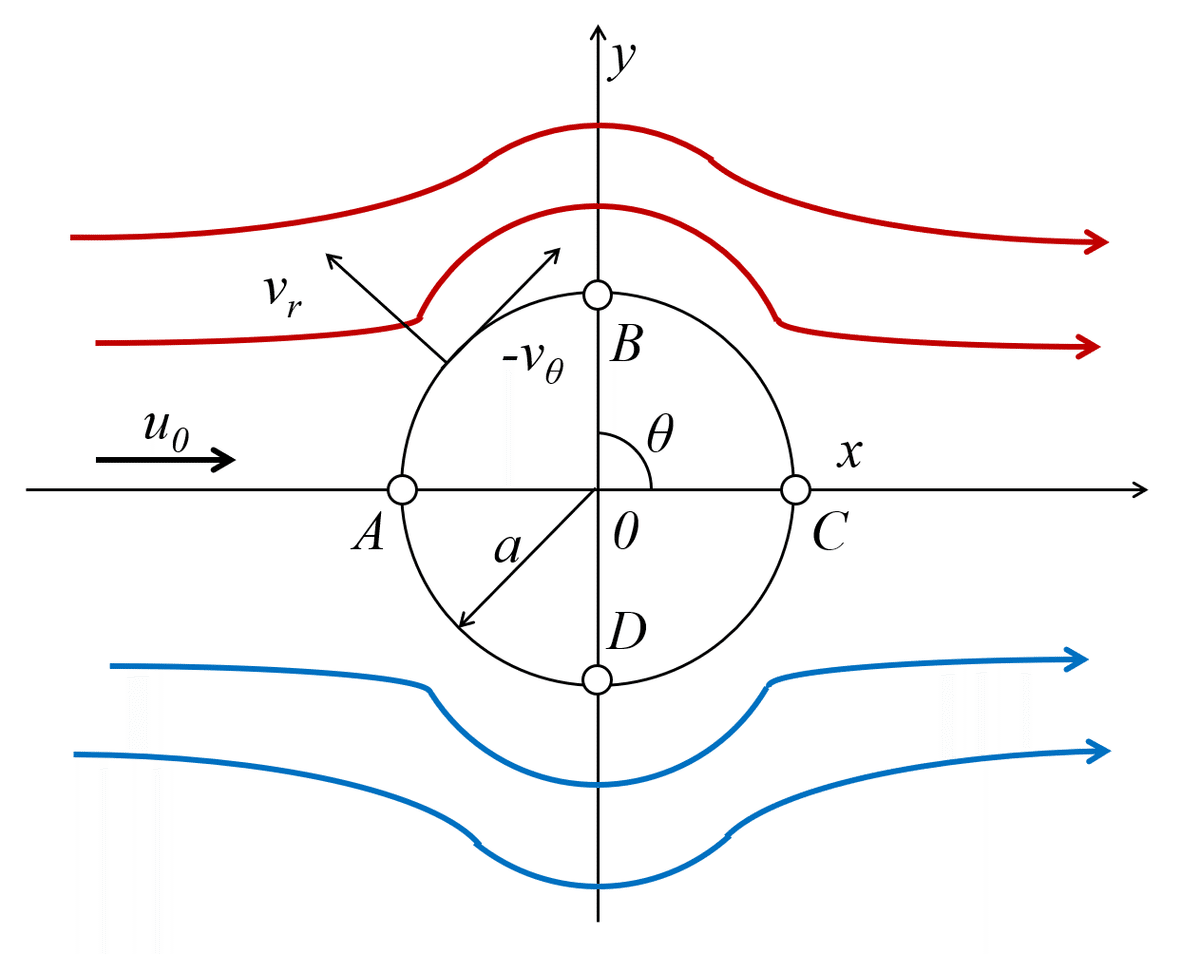
これより,円周上の流速の大きさは,2u0sinθであることが分かり,点A,Cでは速度が「ゼロ」となる岐点(きてん)もしくは,よどみ点といいます。また,点B,Dでは速度が最大値となる角度なので,2u0になります。
ここで少し余談です。このように,円柱の点A,Cではよどみ点となるために速度が「ゼロ」となります。つまり,理想流体中にある物体(今回は円柱)を等速直線運動させたときは,「抵抗力(抗力)」が働かないのです。
抵抗力とはこの場合,円柱をx軸方向に働く外力のことですが,流速がx軸方向に当たっているのに抵抗力が発生していないのは,何だかおかしいくありませんか?
F1などのモータースポーツが大好きな人なところでいえば,「ドラック」です。F1などのとんでもない競技車両でも時速100kmからの加速と時速300kmの加速を比較すると,時速300kmではほとんど加速できませんよね。あれが「抗力」であり,実際の現象として抗力が働いているのです。
このように,一見直感に反する事実を「パラドックス」といいます。18世紀に活躍したジャン・ル・ロン・ダランベールという暇人が初めて提唱したことから,理想流体中にある物体を等速直線運動させたときに抵抗力が働かない現象を「ダランベールのパラドックス」と呼ぶことがあります。
この原因は,理想流体では「粘性を考慮していない」です。つまり,流体の持つ粘性がもろに抗力に影響を及ぼすことを意味しているのです。現代においては,この問題は粘性を考慮することで抗力を算出することできており,既に解決しております。
次に,円周上の圧力(静圧)を求めましょう。円柱よりも十分に離れたところの圧力は大気圧と同じと仮定してp0と置きます。詳しい証明は別の機会としますが,圧力と流速の関係は相関関係となることを示した「ベルヌーイの定理」と式(8),(9)を使うと,式(10)が得られます。

ここで,圧力差から速度エネルギー(動圧と同様)で割ったものを「圧力係数」といいます。円柱周りの圧力係数は,図4のようになるといわれています。

円柱に一様流れが直接あたる角度θが小さいと圧力係数は「正」となり,角度θが大きくなると圧力係数が「負」となります。
これは,圧力係数の影響因子が角度θだけであり,sinであることから0°→90°に進角するにつれて,sinθの値は0→1となります。つまり,式(10)から分かるように,(sinθ)^2 = 0.25のときに圧力係数が「ゼロ」となります。計算すると,θは30°となります。
よって,0°~29°,151°~180°では圧力係数は「正」となり,31°~149°では圧力係数は「負」となります。このグラフが描けるということは,圧力(静圧)が負圧,または正圧なのかが判定できます。圧力係数が負の領域であるということは,静圧は正圧となるので,流線は円柱にわき出す格好になります。一方で,圧力係数が正の領域であるということは,静圧は負圧となります。
(4)まとめ
今回の記事のまとめを以下に示します。
① 円柱周りの流れは,一様流れと2重わき出しの合成と同様である。
② 円柱周りの複素ポテンシャルは,平板周りの複素ポテンシャル(一様 流れ)とジューコフスキー変換を使って,複素ポテンシャルと流れ関数を導出可能である。
③ 円柱周りの流速は算出可能であるが,ダランベールのパラドックスがそんざいするため,粘性を考慮しなければならない。
④ 円柱周りの正圧は算出可能であり,圧力係数を使った評価を行う。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「シュワルツ・クリストフェルの定理」について,解説する予定です。
いいなと思ったら応援しよう!

