流体力学　渦周りのポテンシャル流れ（その3）

　皆様おはこんばんちは。そして，お疲れ様です。

 　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第39回目は，前回の予告通り「渦周りのポテンシャル流れ」について紹介していきます。

 

（１）渦周りのポテンシャル流れについて

 　では，「渦周りのポテンシャル流れ」について，解説していく訳ですが，連載企画となります。最近の筆者自身の流行りという訳でもありませんが，以下に解説していく順番を示します。

（ⅰ）強制渦
（ⅱ）自由渦
（ⅲ）原点より半径における圧力変化
（ⅳ）2次元流れにおける中心静圧ｐ
（ⅴ）渦周りの複素ポテンシャル
（ⅵ）渦周りのポテンシャル流れの応用例（ビオ・サバールの法則）

 　渦については，過去の記事にて紹介していますので，気になる方はチェックしてみて下さい。今回以降の記事は，数学的な議論がメインとなります。そして，「渦周りのポテンシャル流れ（その3）」では，（ⅴ）渦周りの複素ポテンシャルを取り上げていきます。

  

（２）渦周りの複素ポテンシャル

 　その3にて，ようやく本題である「渦周りの複素ポテンシャル」に入ります。長い道のりでしたが，やっていきましょう。「渦周りの複素ポテンシャル」とは，2次元流れの原点に循環Γがある流れを想定します。但し，他には渦が存在しない単独の渦のときを考えます。

 　まず，使う式については，3つ存在します。

　1つ目は，循環と周速度の関係式です。単独の渦でかつ渦の中心が原点にある場合を想定できるために利用します。

　2つ目は，渦度の式です。これは，極座標変換したナビエ・ストークス方程式（N-S方程式）から導き出させるものです。

　3つ目は，複素ポテンシャルを求めるのに必要なコーシー・リーマン方程式（C-R方程式）です。これについては，複素関数論で必ず出てくる高等数学であり，過去にも記事として取り上げていますので，確認してみて下さい。

（2-1）式による証明

 　では，早速証明していきましょう。前項でもかいた通り，「渦周りの複素ポテンシャル」とは，2次元流れの原点に循環Γがある流れを想定します。  　つまり，渦周りの流れは，渦の影響により渦を中心として円運動します。渦の中心を原点にとり，原点より半径における周速度vθとすると，円周上の循環は，渦の循環と同様と考えられます。よって，循環と周速度の関係式が使えるため，式（1）のように表せます。

　ここで，2次元流れ，定常流れかつ非圧縮性流体であると仮定すると，渦度の式が利用できます。但し，渦の流れでは，半径方向の速度vrが存在しないので，vr=0が成立します。よって，渦度の式は式（2）のように表せます。

　したがって，式（２）がいわゆる「渦周りのポテンシャル流れ」と呼ばれるものになります。しかし，最終的には，複素ポテンシャルまで踏み込むため，ここで終わりではありません。C-R方程式を利用すると，周速度vθは，式（３）のように表せます。

　ここで，循環と周速度の関係式である式（1）の結果と式（３）の結果から，式（4）のように考えることが出来ます。

　式（４）のr，θについて積分すると，式（５）のように表せます。（※積分定数Cは，「あえて」省略しています。）

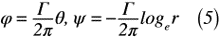
　よって，得られた速度ポテンシャルφと流れ関数ψを使って，複素ポテンシャルw(z)を求めると，式（６）のように表せます。

　式（６）が，渦周りの複素ポテンシャルの最終結果となります。複素関数の中では，z平面上の対数関数は，円を描きます。つまり，渦が外的要因で乱されることがなければ，ただの円となり，半径によって渦の大きさが決まるということです。

　これが分かると，対数関数の前についている定数は，ただの渦の強度を表すだけのものであることも分かります。しかも，渦の強度に影響するのは，循環Γだけであるということです。

  

（3）まとめ

 　今回の記事のまとめを以下に示します。
（１）渦周りの複素ポテンシャルは，循環と周速度の関係式，渦度の式およびC-R方程式によって導き出させる。
（２）得られた式から，複素数z(=re^iθ)が大きくなると，渦の大きさが大きくなり，循環Γが大きくなると，渦の強度が大きくなる，いずれも比例関係が成立する。

以上です。最後まで閲覧頂きありがとうございました。

 ※次回は，「渦周りのポテンシャル流れ（その4）」を取り扱う予定です。