
補足編 コーシーの積分定理
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,次回以降に投稿予定の「ブラジウスの第1公式」,「ブラジウスの第2公式」の解説で使用する「コーシーの積分定理」について取り上げてみようと思います。
(1)コーシーの積分定理とは
今回は,コーシーの積分定理を紹介していきます。この定理は,別名「コーシーの第1定理」とも呼ばれることがあり,この定理を導き出した暇人こそ,オーギュスタン=ルイ・コーシー(Augustin Louis Cauchy, 1789~1857)というフランスの数学者です。コーシーは,数学者として特に現在では「解析学」と呼ばれる学問で多大な功績を残した人であり,過去に記事で取り上げた「コーシー・リーマンの微分方程式」も彼の功績の1つです。その他,知っている人であれば,「コーシーの〇〇」のような公式や定理が出てくるほど,彼の功績は大きなものです。

(参考:Wikipediaフリー百科事典)
さて,コーシーの積分定理は端的にいうと,とある閉曲線上の複素関数w(z)が正則,かつ連続な導関数であるときの1周線積分が必ず「ゼロ」になるという定理です。正式に以下のような言い方をします。
「単純閉曲線(始点と終点以外に交点を持たない閉曲線)Cで囲まれた内部領域Dと置くと,複素関数w(z)が単純閉曲線Cかつ内部領域Dで正則,かつ連続な導関数のとき,式(1)が成立する。」

では,式(1)が成立するかどうかを証明してみましょう。単純閉曲線Cとその内部領域Dで正則な複素関数w(z)=φ+iψと複素数z=x+iyと置くと,複素関数w(z)の単純閉曲線Cに沿った1周線積分は,式(2)のように表されます。

ここで,以前の記事で紹介した「ストークスの定理」を使います。
但し,使用するにあたって注意があります。ストークスの定理は,微小な面要素の総和が外周Cの周積分に等しいことを証明したものです。ここで,微小な面要素の総和をそのまま使用すると都合が良くないので,微小な面要素の総和から単純閉曲線Cの面積素の総和に変更します。
これを「平面のグリーンの定理」といい,ストークスの定理の特殊な場合として使うことが出来ます。よって,ストークスの定理の特殊な場合である「平面のグリーンの定理」は式(3)のように表されます。

では,式(3)を式(2)に代入すると,式(4)が得られます。

式(4)を更に式変形するには,コーシーの積分定理の文言で大事な言葉に注目します。「正則」です。複素関数が正則であれば,以前の記事で取り上げたコーシー・リーマンの微分方程式(以下,C-R方程式)が使えます。
そこで,式(5)にC-R方程式を示します。

式(5)を式(4)代入すると,式(6)のように表されます。

この式(6)は,式(1)と同じ式,すなわちコーシーの積分定理が証明できたことになります。コーシーの積分定理は,多くのパターンでも成立することが分かっていますので,次項ではそのパターンに注目してみましょう。
(2)積分路変形の原理
ここでは,コーシーの積分定理が成立するパターンの1つ目を見ていきましょう。図1に2点a,bを両端とする2つの曲線C1,C2がある場合の図形を示します。

コーシーの積分定理(式(1),または式(6))が成立することを前提に考えたうえで,図1の積分経路を数式化すると,式(7)のように表されます。今回は,a→bまでの経路を「プラス」として考えて,逆にb→aまでの経路を「マイナス」として考えることにします。

式(7)は経路によって,符合が変わることを用いて,始点と終点が同じであれば,経路が異なっていても(積分路変形),コーシーの積分定理が成立することを意味しています。これを「積分路変形の原理」と呼ぶこともあります。数式だけ見ると,線形性(加減法を使っただけ)が利用可能であることを述べただけですが,とても重要なのです。
(3)2重連結領域
コーシーの積分定理が成立するパターンの2つ目を見ていきましょう。図2に閉曲線C1の外部に他の閉曲線C2があり,複素関数w(z)は閉曲線C1,C2の上およびその間で正則である場合の図形を示します。(C2>C1)
図2のような状態を「2重連結領域」と呼びます。

およびその間で正則である場合(2重連結領域)
ここで,コーシーの積分定理が成立することを前提に考えたうえで,図2の積分経路を数式化すると,式(8)のように表されます。今回は,図2に示した反時計周りを「プラス」として考えることにします。

式(8)より,始点と終点が同じであれば,コーシーの積分定理が成立する積分路変形の原理を用いると,式(9)のように書き換えが出来ます。

線分ABと線分A’B’に注目し,両者の辺の長さが同じでかつ極限まで線分AA'と線分BB’の間を省略できるまで短くすると,式(10)に示すように取扱いの都合が良くなります。

また,線分AA‘と線分BB’を省略できるまで短くすると,式(11)のように表され,式(10),(11)を式(9)に代入すると,式(12)のようになります。


式(12)は,閉曲線C1の外部に他の閉曲線C2が存在するとき(2重連結領域)でも,コーシーの積分定理の積分定理が成立することを意味しています。
(4)単一閉曲線内部に半径rとなる円Kを境界とする2重連結領域
コーシーの積分定理が成立するパターンの3つ目を見ていきましょう。図3に単一閉曲線Cの内部に半径rとなる円Kを境界とする2重連結領域の図形を示します。また,複素関数はw(z)=(z-z0)^nとします。(n:正負の整数)
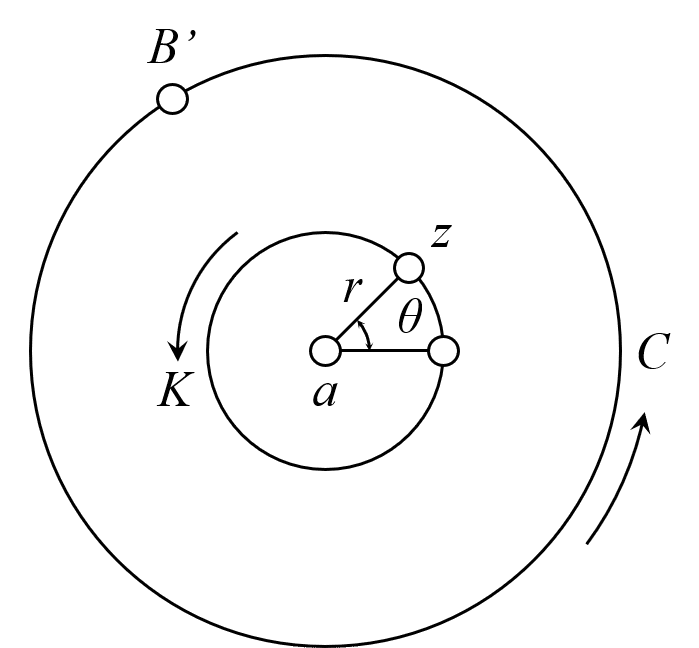
コーシーの積分定理(2重連結領域)を利用すると,式(13)のように表されます。

ここで,点aは原点からのズレ量と考えると,複素数z-a=re^iθ,複素数の微分dz = ire^iθdθとなるため,式(13)を書き換えると,式(14)のようになります。

式(14)を見ると,sinとcosで構成されているので,両者をそれぞれ0~2πの領域(円1周の領域)で積分すると,以下の式(15)のような結果が得られます。

式(15)を式(14)に代入すると,式(16)のようになります。

式(16)の結果から,n=-1の場合のみ複素関数w(z)=(z-z0)^nの積分値が「2πi」となり,n=-1以外の値の場合は複素関数w(z)=(z-z0)^nの積分値が全て「ゼロ」となるのです。
もし,点aは原点からのズレ量と考えずa=0の特別な場合であっても,複素関数w(z)=z^nの積分値は,n=-1の場合のみ「2πi」となり,n=-1以外の値の場合は,式(17)のように全て「ゼロ」となります。

よって,式(16),(17)の結果から,コーシーの積分定理は,n=-1の場合のみ積分値を持つことになり,n=-1以外の値の場合は全て「ゼロ」となります。
(5)まとめ
今回の記事のまとめを以下に示します。
① コーシーの積分定理を導き出したオーギュスタン=ルイ・コーシーは,フランスの数学者であり,解析学で多大な功績を残した。
② コーシーの積分定理の導出には,ストークスの定理の特殊な場合である平面のグリーンの定理とコーシー・リーマンの微分方程式を用いる。
③ コーシーの積分定理は,積分路変形や2重連結領域でも成立するが,一閉曲線Cの内部に半径rとなる円Kを境界とする2重連結領域の場合のみ,特殊なパターンが存在する。
以上です。最後まで閲覧頂きありがとうございました。
※本記事は,「ブラジウスの第1公式」,「ブラジウスの第2公式」にて利用する背景知識となります。
いいなと思ったら応援しよう!

