
流体力学 ポテンシャル流れの合成
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第16回目は,第15回目で予告した通り,「ポテンシャル流れの合成」について紹介していきます。
(1)ポテンシャル流れの合成
さて,今後の記事で取り上げる予定の「合成」についてですが,基になる理論として「重ね合わせ」があります。この「重ね合わせ」は物理学ではよく使われます。そのため,使われる頻度が高いために,重ね合わせが使えて「当たり前でしょ?」と思われるものになっているかと筆者は考えています。しかし,今回はこれが当たり前ではないのことを紹介し,結論としてポテンシャル流れでは「重ね合わせ」が利用できるため,流れを「合成」できるのことを書いていきます。
では,結論から述べましょう。適当な複素ポテンシャルw1(z)とw2(z)を用意したとき,式(1)のように表せます。
但し,φは速度ポテンシャル,ψは流れ関数をそれぞれ示します。
(2)重ね合わせ
(2-1)成立条件
では,先ほどのキーワードである「重ね合わせ」ができれば,「合成」ができることを書きました。物理学でよく使われる「重ね合わせ」ですが,共通して使える考え方は,以下の通りです。
「重ね合わせ」ができるものは,取り扱うものがすべて「線形」のみである!
これが結論です。ここでは,「線形」を知るためには,「非線形」の存在を知る必要があります。両者の関係は,いわゆる対義語なのです。以下に両者の説明をざっくり書きます。
「線形」は,時間が経過するにつれてグラフの形が変わらないものを指します。例えば,初等関数として挙げられる「1次関数」,「2次関数」や「三角関数」などがこれに該当します。
一方で,「非線形」は,時間が経過するにつれてグラフの形が変わるものを指します。研究や講義等の実験で測定した結果を見てみても,多くの現象がこのような「非線形」が大半を占めますが,現象を簡単にするため(専門的には,モデル化するなどという)に,時間変化を考えないことが多いのです。ちなみに流体力学では,線形のときを「定常流れ」,非線形のときを「非定常流れ」といいます。
よって,ポテンシャル流れの「重ね合わせ」ができるということは,「線形」であることが証明できること(数学的には,満足していることと書かれる)が必要です。では,ここで,ポテンシャル流れに登場するものを思い出しましょう。用語すら聞いたことがない方は,以前の記事をご覧ください。
(2-2)速度ポテンシャル
ポテンシャル流れで登場するものは,速度ポテンシャルφ,流れ関数ψの2つです。この2つが「線形」であることが証明できれば良い訳です。では,この証明をしてみましょう。
まずは,速度ポテンシャルの証明からです。noteではまだ解説していませんが,微小流体要素を考えたときに使う考え方の1つに「連続方程式」,通称「連続の式」というものがあります。ここで,時間変化しない流れの「定常流れ」,流体の密度が変化しない「非圧縮性流体」,かつ「2次元流れ」であると仮定するときは,式(2)のように表せます。

ここで,式(3)にコーシー・リーマンの微分方程式を示します。
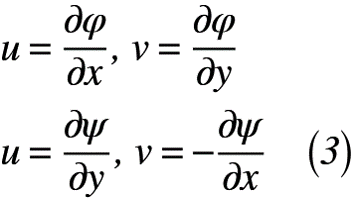
では,式(3)を式(2)へ代入すると,式(4)のように表せます。

この式(4)がいわゆる「ラプラス方程式」と呼ばれるものです。見て頂ければわかる通り,時間変化による項が存在しないため,速度ポテンシャルφは,ラプラス方程式を満足していることから,「線形」であるために「重ね合わせ」が適用できるのです。メタな話をすれば,「連続の式」の仮定で「定常流れ」としている時点で「線形」となることが確約されているのですが…。
(2-3)流れ関数
次に,流れ関数の証明です。以前の記事で取り扱った「渦度」の考え方を使います。連続の式と同様に,時間変化しない流れの「定常流れ」,流体の密度が変化しない「非圧縮性流体」かつ「渦無し流れ」を考慮すると,渦度ζzは,式(5)のように表せます。
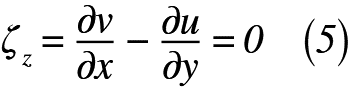
では,速度ポテンシャルと同様に,式(3)を式(5)へ代入すると,式(6)のように表せます。
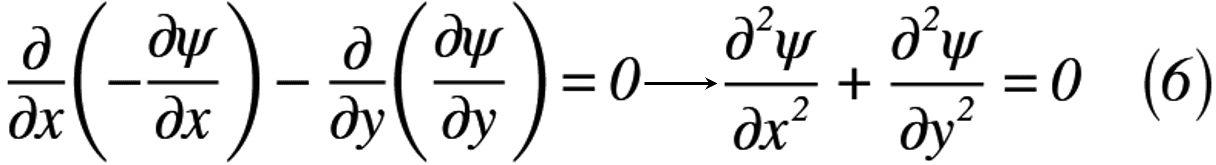
よって,式(6)も式(4)と同様に「ラプラス方程式」を示しています。そして,時間変化による項が存在しないため,流れ関数ψは,ラプラス方程式を満足していることから,「線形」であるために「重ね合わせ」が適用できるのです。これらは,すべて過去の記事で紹介したものが集約されています。今回扱ったもので不明なものについては,過去の記事をご覧ください。
(3)まとめ
今回の記事のまとめを以下に示します。
(1)「重ね合わせ」が利用できれば,複素ポテンシャルの「合成」が可能になる。
(2)「重ね合わせ」の共通の考え方は,「線形」であれば「重ね合わせ」が利用できる。
(3)速度ポテンシャルと流れ関数は,いずれもラプラス方程式を満足していることから「線形」が成立するため,ポテンシャル流れは複数の複素ポテンシャルを組み合わせた「重ね合わせ」が可能である。
以上です。最後まで閲覧頂きありがとうございました。
※次回は,一様流れとわき出しの合成について扱う予定です。
いいなと思ったら応援しよう!

