
流体力学 薄翼の理論(その3)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第67回目として「薄翼の理論(その3)」について紹介します。また,補足編の「薄翼理論の数学」と「薄翼の理論(その1)」,「薄翼の理論(その2)」でお伝えした考え方を使うことでより具体的な4つの影響因子(揚力L,揚力係数CL,前縁周りのモーメントM,モーメント係数CM)を算出することが出来るところまで紹介します。
(1)よく出てきたA0,A1,…,Anとは?
はじめに,A0,A1,…,Anとは何だったでしょうか。解答は,過去記事の「薄翼理論の数学」を再度確認してほしいのですが,「A:未知の級数(フーリエ級数)」でした。
このフーリエ級数とはいっても,過去記事である「薄翼の理論(その1)」,「薄翼の理論(その2)」で証明したときにはあえて触れていませんでした。今回は,このAについての導出を最後の締めとして行ってから,4つの影響因子(揚力L,揚力係数CL,前縁周りのモーメントM,モーメント係数CM)を具体的に算出してみましょう。
さて,「薄翼の理論(その1)」で触れた渦全体で任意のx1点に誘導される速度v(x1)(与式(1))にジューコフスキーの仮定(xとθの関数)と渦分布γのフーリエ級数(xとθの関数)の2つを代入して証明します。

ここで,注意するべきはxの積分範囲をθの積分範囲に変更することです。元々はxが0~Lまでの積分範囲を,ジューコフスキーの仮定(xとθの関数)にxを代入してθが成立するような値を決めると,θが0~πまでの積分範囲に変更します。次に,「薄翼理論の数学」で紹介した定積分の結果を使います。(※n=1と書いたのは,(1-4)定積分の③定積分problem3の積分結果から来ています。)あとは,代入した渦全体で任意のx1点に誘導される速度v(x1)を解いていくと,式(2)のようになります。

ここまで,渦全体で任意のx1点に誘導される速度v(x1)(与式(2))を求めましたが,実際の翼に当たる流れを考慮すると,わずかに傾きを持つことが多々あるので,その傾きと一様流れの速度を考慮した合速度で議論します。(「薄翼の理論(その1)」の式(8)参照。)
翼の傾きdy/dxに渦全体で任意のx1点に誘導される速度v(x1)を代入すると,式(3)のようにvとθの関数に置き換えが出来ます。但し,今回は便宜上θ1をθに変換した結果としております。

次に,A0(フーリエ級数)を算出していきます。式(3)で算出したvとθの関数の両辺にそれぞれ0→πまでを積分すると,A0単体は式(4)のようになります。

最後に,An(フーリエ級数)を算出していきます。本来は,数学の得意な方(数学的帰納法を使った考え方)からすれば,A1を算出してからやるものだと言われそうですが,結局のところAnが分かれば,あとは要らない訳です。そこで,式(3)で算出したvとθの関数の両辺にcosnθを掛けてからそれぞれ0→πまでを積分すると,Anは式(5)のようになります。数学が得意な人は,式(5)こそ「フーリエ余弦級数の係数」だとすぐわかるはず。

従って,式(5)の結果からnの値を任意に決めてやれば,A1だろうとA100だろうと,どんなフーリエ級数でも算出できます。
(2)放物線翼形の4つの影響因子
[例題]薄翼が与式(6)に示すような放物線翼形の場合,揚力L,揚力係数CL,前縁周りのモーメントM,モーメント係数CMを求めよ。


放物線翼形は図1のような概略です。ここで,上図に示したように後縁角βは式(7)のように表せます。
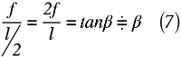
解法としては,以下のようなイメージで考えます。
①ジューコフスキーの仮定 → ②A0,A1,…,An(フーリエ級数)
→ ③4つの影響因子
それでは,解いていきましょう。まずは,ジューコフスキーの仮定を与式(6)の微分した結果に代入すると,式(8)のようになります。

次に,A0,A1,A2(フーリエ級数)を算出します。そのためには,式(8)の結果が不可欠なのです。式(8)を式(4)および式(5)へ代入すると,式(9),式(10),式(11)のように表せます。



最後に,4つの影響因子(揚力L,揚力係数CL,前縁周りのモーメントM,モーメント係数CM)に上記の式(9),式(10),式(11)を代入します。この4つの影響因子に関する証明は,「薄翼の理論(その2)」で触れていますので,今回は既に分かっているとして取り扱います。

この結果より,放物線翼形の4つの影響因子を算出できました。フーリエ級数の係数を具体的に求めましたが,結局のところ迎え角αと後縁角βの2つが影響因子であることが分かりました。
筆者の頭はあまりよくないので,過去の偉人たちが切り開いたものを読み解くだけで精一杯ですが,この形がある程度予測できていないと4つの影響因子を更に式変形しようとは決して思いませんね。
(3)まとめ
今回の記事のまとめを以下に示します。
① 4つの影響因子にあるAはフーリエ余弦級数の係数を示している。
② 4つの影響因子は,ジューコフスキーの仮定からフーリエ余弦級数の係
数を個別に求めることで算出できる。
以上です。最後まで閲覧頂きありがとうございました。
次回の記事では,「翼列」を取り上げる予定です。
但し,年末年始の記事で予告した通り,次回の更新は3月以降になりそうです。読者の不特定多数の皆様は,気長に首を長くしてお待ちいただけると嬉しいです。
いいなと思ったら応援しよう!

