
流体力学 ブラジウスの第1公式
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
今回は,第59回目として「ブラジウスの第1公式」について紹介したいと思います。
(1)ブラジウスの公式
今回は,ブラジウスの第1公式を紹介していきます。この定理を導き出した暇人こそ,ポール・リチャード・ハインリヒ・ブラシウス(Paul Richard Heinrich Blasius, 1883~1970)というドイツの流体力学・物理学者です。ブラジウスは,流体力学の専門家として現在のハンブルク応用科学大学(Hamburg University of Applied Sciences)で高等教育と研究活動に励んでいたそうです。

(参考:Blasius A life in research and education, Hager, Willi H., 2003)
流体力学が大好きという方には,同じくドイツの流体力学・物理学者であるルートヴィヒ・プラントル(Ludwig Prandtl, 1875~1953)という偉大なる暇人が師範だったそうです。(ブラジウスにとっては,プラントルは先生だった)ブラジウスといえば,粘性流体では境界層について,水力学では管内の乱流について,彼の名前を聞くのではないでしょうか。それほど,ブラジウスの功績は現在の流体力学においても非常に大きなものといえます。
さて,ブラジウスの公式(1910~1911)はよく第1公式と第2公式に分けられます。具体的には,「2次元非圧縮性理想流体の渦無し定常流れ」が成立するとき,第1公式は物体に働く「圧力」を求めたものです。また,第2公式は物体に働く「(曲げ)モーメント」を求めたものです。
(2)公式の有効性
前項のブラジウスの公式ですが,正直なところ何がすごいのかよくわからない方が多いのではないでしょうか。かくいう筆者もこの勉強をしたとき「圧力とモーメントがわかって何が得するのだろう…」と思っていました。そこで,過去に設計技術者として働いた筆者がそのときの経験則からこの問いに解答してみます。但し,説明に材料力学(構造力学)の話が急に登場しますが,ご了承ください。簡単に言うと,材料力学(構造力学)は「物体に作用する力や曲げモーメントによって,発生した応力をあらゆる方面から計算する学問」です。
結論からいうと,「圧力や曲げモーメントが分かることで物体に発生する応力で議論ができる」ことです。具体的には,「設計した構造物に発生する応力が許容応力(材料が破損しないギリギリの応力のこと)以下かどうかを求めるのに,圧力および曲げモーメントが必要となる」からです。
では,この結論に対する説明をしていきます。図1に部材に作用する形態を示します。

図1の力(軸方向力およびせん断力)と曲げモーメントは右に示した式で応力・圧力を求めます。ここで,P:圧力,σ:応力,F:力(軸方向力およびせん断力),A:面積,M:曲げモーメント,I:断面2次モーメント,y:中立軸から求めたい応力までの距離,Z:断面係数,σa:許容応力を示します。
重要なことは,各文字をすべて理解することではなく,面積A,断面2次モーメントI,距離y,断面係数Zの4つが材料の形状によって決まることです。つまり,発生する応力σに対して破損しないようにするには,面積Aと断面係数Zを大きくすることで発生する応力σを小さくできます。すなわち,力Fや曲げモーメントMが算出できると,面積Aと断面係数Zを使って発生する応力σが求められ,許容応力以下であるかのチェックができます。だからこそ,ブラジウスの公式は第1公式で「圧力」,第2公式で「モーメント」を算出できることが,設計するうえでとても有効なのです。ちなみに,圧力Pと応力σは同じ単位(単位面積当たりの力[N/mm^2])です。但し,すみ分けとして,「応力」は「固体」に適用する(材料力学・構造力学で使う)ものに対し,「圧力」は「液体・気体」に適用(熱力学・流体力学で使用)します。
1910年は,人類が初飛行を遂げた立役者ライト兄弟によって,飛行機を製作する会社(Wright Company)が創立した頃です。この頃から航空機の理論や設計に関することが急速に発展していくので,ブラジウスはすごい方(暇人)なのです。
(3)ブラジウスの第1公式
では,ブラジウスの第1公式を導出してみましょう。図2にz平面における任意断面を柱状体の概略図を示します。

このとき,流れが物体(柱状体)に働く全圧力x,y方向をそれぞれPx,Pyとすると,式(1)のようになり,この式(1)こそ「ブラジウスの第1公式」なのです。

先ず,柱状体(単位長さ1とした2次元)の周辺の任意の1点より,図2のような三角形を考えます。このとき,ds;線素,dx:x方向成分の線素,dy:y方向成分の線素,α:任意の角度,pds:dsに対して垂直に働く流体の圧力による力を示します。この三角形(柱状体)に働く全圧力のx,y方向は,式(2)のようになります。

ここで,三角関数の定義に立ち返ると,式(3)のように考えることが出来ます。

得られた式(3)を式(2)へ代入すると,式(4)に書き換えられます。

このとき,柱状体(三角形)周辺に沿って流れる流速qsと置くと,ベルヌーイの定理(定常流れのとき,物体の前後で運動エネルギーと圧力エネルギーがエネルギー保存側によって成立する定理)は,式(5)のようになります。

式(5)を式(4)へ代入すると,式(6)のようになります。
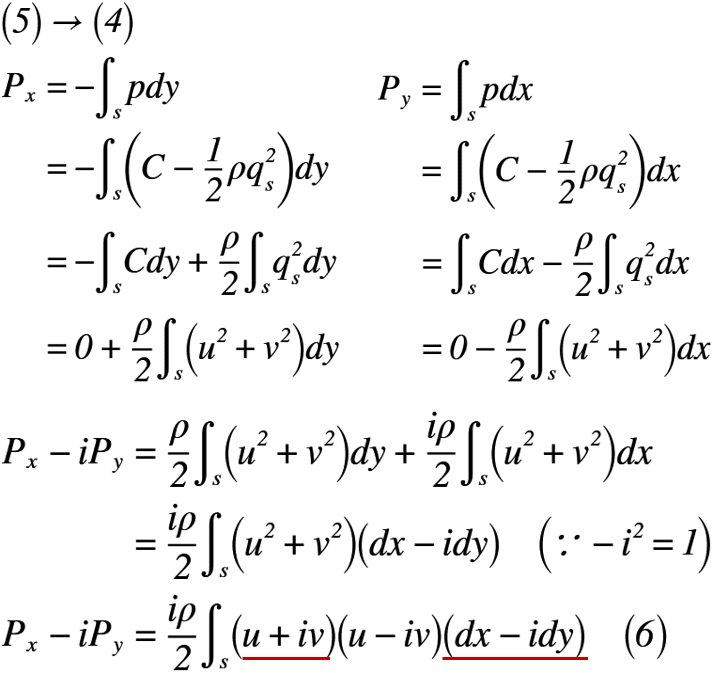
式(6)の形は,下線部で示したように微分記号があって気持ち悪いので,さらに書き換えます。以前の記事で取り上げた「流線の式」を使用します。
式(7)に流線の式を示しますが,詳細が知りたい方は過去の記事をご確認ください。

では,式(7)を式(6)の下線部に適用すると,式(8)のようになります。

式(8)に注目すると,右辺の積分は,柱状体周辺に沿っての1周積分です。この話は,過去の記事で取り上げた「コーシーの積分定理」が使えます。詳細は,過去の記事をご確認ください。
つまり,コーシーの積分定理によって,柱状体周辺を囲む任意の閉曲線Cの間に(dw/dz)^2の特異点(正則でない点,すなわち微分不可能な点)がない場合は,柱状体周りの長さsに沿う積分を任意の閉曲線Cに沿う積分に置き換えが出来ます(過去記事の「2重連結領域」に該当する)。以上の話を用いて,式(8)の1周積分の場所を置換すると,式(9)のようになります。
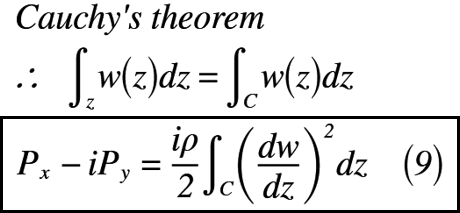
式(9)は,式(1)と同様の式になったことから「ブラジウスの第1公式」が導出できました。ここで,w:柱状体周りの流れの複素ポテンシャル,ρ:流体密度,C:柱状体を囲む任意の閉曲線を示します。具体的にブラジウスの第1公式を使用して,圧力を求めた結果については,次回の記事へ持ち越します。
(4)まとめ
今回の記事のまとめを以下に示します。
① ブラジウスは,第1公式および第2公式を導き出した以外に,境界層や管内の乱流に関する功績も残す流体力学者である。
② ブラジウスの第1公式および第2公式は,翼の設計をするうえでも有効性の高い公式である。
③ ブラジウスの第1公式は,物体に働く「圧力」を求めるものであり,ベルヌーイの定理とコーシーの積分定理を用いて導かれる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「ブラジウスの第2公式」について取り上げます。
いいなと思ったら応援しよう!

