流体力学　カルマン渦列（その3）

 　皆様おはこんばんちは。
 
　流体力学を再度学び直してみようと思い，記事にしています。
　第46回目は，「カルマン渦列（その3）」について紹介していきます。なお，カルマン渦列は連載企画となので，その1とその2をご覧になっていない方は是非記事を参照してください。
　文だけ書いておいて，余裕で1ヶ月以上も放置プレイしている筆者のことはスルーしてください。
 

（1）カルマン渦列の安定度

　前回（その2）では，対称型渦列と非対称型渦列を取り上げました。下記に記事を載せておきますので，この記事の内容を既に知っている前提で進めます。

　これらの渦列は，影響を及ぼす因子が同じであることまで紹介しました。次に，気になるのは「渦の安定度」です。ここでの「安定度」とは，何を指しているかについて説明します。
　カルマン渦列は，基本的に循環Γが同じ，すなわち渦の強度が同じで配置が元の位置から変わらずに流れに乗って渦列が移動するものです。しかし，その規則的な渦列の配置は，外乱（この場合，流れの速度が変わったり，流れの向きが急に変わったりなど）によって，渦列の配置が変わっても，時間経過とともに元の配置に戻る渦列を「安定」と考えます。

　一方で，「不安定」とは外乱によって，渦列の配置が変わった後に元の配置に戻ることがない渦列のことを指します。
　ちなみに，安定と不安定の中間状態も存在します。この状態は，完全に元の状態に戻らないものの大幅に渦列の配置が崩れずに元の配置に限りなく近い配置のことを指します。そして，安定性の検討で，対称型渦列は「不安定」，非対称型渦列は「安定」であることが証明されており，渦間間隔aとbのアスペクト比が「b/a = 0.2806」で「安定」となるそうです。今回，数学的な議論は省略させて頂きましたが，物体の後部に発生するカルマン渦列に焦点を当てていきましょう。
（※この理論は，かなり難解なので筆者は断念しました…。出来たら，また別記事とさせて下さい。）

（2）物体後部のカルマン渦列

　前項でさらっと物体後部にカルマン渦列ができると言いました。これは，流れ場を実験的に観測して得られた経験則に基づくものです。特に，カルマン渦列は周期性のある渦列であり，後部が尖っていない場合によく生ずるそうです。物を設計するときの思想として，尖ったものは嫌う傾向があります。
　例えば，「人が刺さって危ない」，「塗装やメッキなどの表面処理が剥離しやすくなる」や「ボルトや溶接などの接合しづらい」などのトラブルが頻発するため，世の中の工作物は一般的に先端部（前部，後部含める）が尖っていないものがほとんどということになります。つまり，世の中にあるもののほぼすべてが後部に渦が発生しやすいということになります。

　よく使う物体の形状は，図1に示すような「円柱」，「角柱（平板）」と「流線形（翼）」の3点となります。

図1　各物体の形状

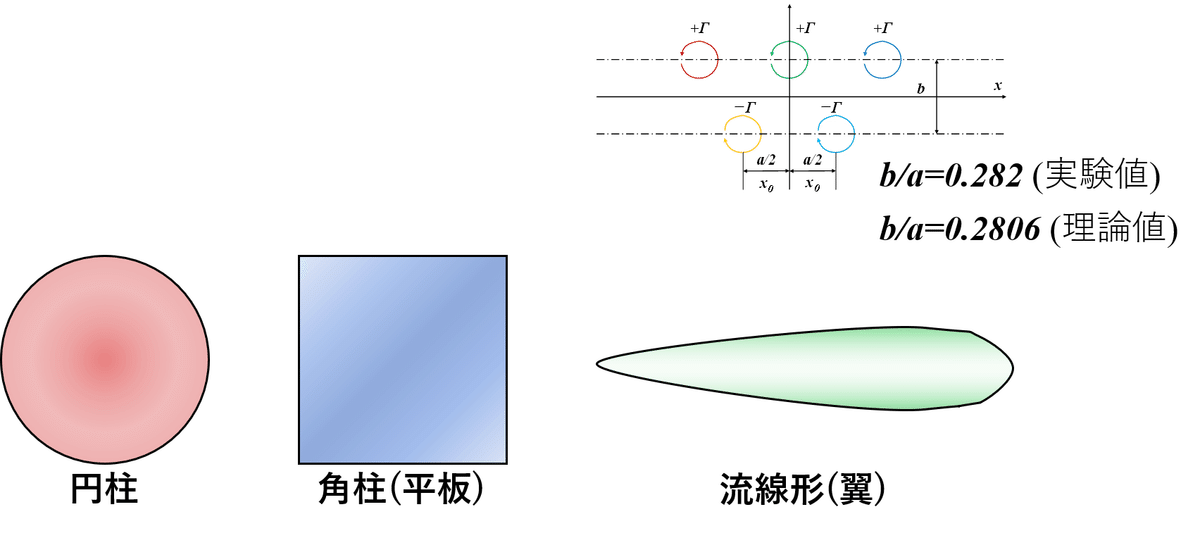
　物体の形状はかなり異なるように思いますが，風洞実験による実験結果として，渦間間隔aとbのアスペクト比は「b/a = 0.282」となり，数学的に求めたアスペクト比と「b/a = 0.2806」と理論的な結果とも一致するそうです。つまり，渦間間隔aとbのアスペクト比が一定とすることで他の新たな影響因子がある可能性を示唆していることになります。

　そこで実験を重ねて出てきたものは「流体振動」と呼ばれるものです。これは「ストローハル数」という周波数（単位時間にできる渦の組数）と同様の考え方をした定量評価を行います。
　次項では，ストローハル数について触れます。 

（3）ストローハル数

　前項で取り上げたストローハル数とは，単位時間にできる渦の組数f（2列の渦を1個ずつ取って1組とする）のことです。つまり，単位時間経過後にf組の渦ができるかを指しており，渦の組数が多いとより振動しやすい環境となっていることは容易に想像できます。
　ストローハルは，「ヴィンツェンク・ストルーハル」というチェコの物理学者から来ています。振動する流れのメカニズムを解明した彼の功績であるストローハル数は，風の中でワイヤーが流体力学的にどのような影響があるかを実験しているときに得られた結果だそうです。おそらく，ワイヤーのようにものでも流れがあるところでは，物体が振動することを明確に捉えていたのでしょう。すごいですね。

　では，図2のように円柱の後部にカルマン渦列が非対称型渦列で生成させていると考えます。

図2　物体後部の流れ場

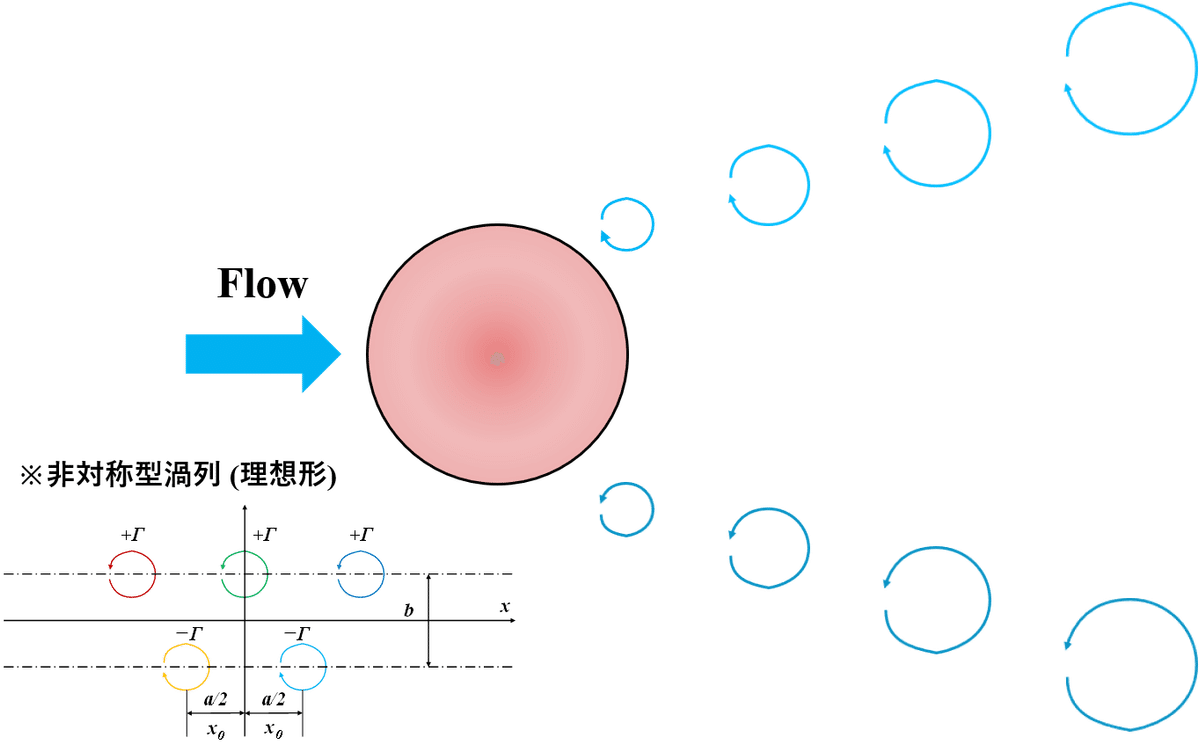
　流れ場の流速u，渦列の流速U (u<<U)の場合，流速と渦列の相対速度がx軸方向の渦間間隔aと渦の組数f（周波数に該当する）の掛け算とつり合いが取れるので，式（1）が得られます。

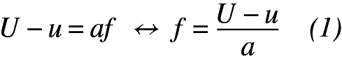
　次に，渦間間隔aとbのアスペクト比（b/a = 0.282），渦間間隔bと円柱の代表長さの比（b/D = 1.2）および流れ場の流速uと渦列の流速Uの比（u/U = 0.14）の場合，渦の組数fを求めると，式（2）のようになります。

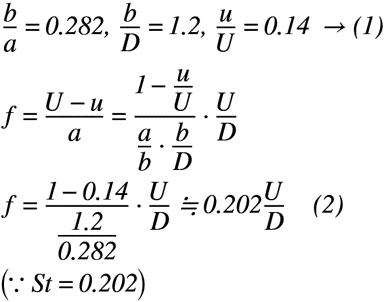
　ちなみに，「円柱」，「角柱（平板）」と「流線形（翼）」で多少は異なるのですが，各ストローハル数は式（3）の一覧のようになり，0.2程度となります。

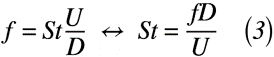
　これにより，速度分布が変化してしまうため，圧力分布も必然的に変化するために振動する現象につながります。悪いことに，この振動数が物体の持つ固有振動数（見る振動数によっても異なるが，機械設計では，この振動数付近にはしない，あるいは瞬間的になる程度にする）と一致することで，大きな風切り音が発生する，共振現象によって物体が破壊するなど重大な公害や損傷を引き起こします。
 
　ここで，流体力学では必ず出てくる必須用語に「レイノルズ数」があります。この定量評価によって，流れ場が層流か乱流かを判断する指標となっており，代表速度Uと代表長さDが影響因子となっております。参考までに，式（4）にレイノルズ数の算出式を示します。

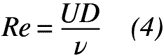
　式（4）でも出てきたように，速度Uと長さ（円柱なら直径に該当する）Dの比がストローハル数にも出てきます。つまり，同じ影響因子があるということは，レイノルズ数とストローハル数は密接な関係があることが想像できます。
　と思いきや，レイノルズ数とストローハル数はほぼ無相関であることが知られています。レイノルズ数の増加に伴って，ストローハル数は0.2～0.3程度に増加するのですが，渦の組数fを計算する際には，ほとんど影響がないですよね。なので，実際に設計に使うときなどもストローハル数は0.2程度としてざっくり計算しても差し障りないということなのでしょう。

　最後に，レイノルズ数がどのくらいで振動するかについてですが，答えは「わからない」です。過去に多くの方々が実験しているため，円柱の場合はレイノルズ数が50から振動しはじめるそうですが，人によって変わるのが現状です。いかに流れ場を制御しても，ランダム要素が大きいのが「流体力学」だと思わせる事象です。

（4）まとめ

今回の記事のまとめを以下に示します。
（１）カルマン渦列が安定する理論的な条件は，非対称型渦列で渦間間隔aとbのアスペクト比が「b/a = 0.2806」の場合である。
（２）カルマン渦列が安定する実験結果は，渦間間隔aとbのアスペクト比は「b/a = 0.282」であり，形状による影響は少ない。
（3）ストローハル数はどの形状でも0.2程度となり，代表速度Uと代表長さDによって，単位時間にできる渦の組数f（周波数）が決定される。

　以上です。最後まで閲覧頂きありがとうございました。
 　次回は，「等角写像」について，解説する予定です。