
流体力学 複素ポテンシャルの極座標変換
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第9回目は,第7回目でネタにした「複素ポテンシャル」の補足についてかいていきたいと思います。前回の「複素ポテンシャル」をまだご覧になっていない方は,以下の記事を見てみてください。
※今回の記事は,かなり数学的な説明が多いため,数式が羅列することになることを予めお伝えしておきます。
(1)スルーしてはいけない記事の一文(2回目)
完全に前回の「複素ポテンシャル」を知っている人,あるいは記事を見て頂いた方に限定してしまい,大変申し訳ございません。ですが,あの記事でスルーしていけない一文が2カ所もあるのです!
今回は,その2つ目を取り上げます。では,その一文とはどこなのでしょうか?
以下に答えとなる一文を示します!
「極座標(r,θ)へ座標変換した場合の速度成分は,式(6)のように表せます。」
この一文で「いきなりどうした。」とか,「何で急にその式が出てきた?」と思った人は,「良く気づきましたね!」との一言を送ります(笑)。
ここでスルーしてはいけないのは,「直交座標系から極座標へ変換すること」なのです。さも当たり前のように言っているのですが,全然当たり前ではありません!
これは,以前に取り扱った「コーシー・リーマンの微分方程式(以下,C-R微分方程式)」と「複素ポテンシャル」を題材に「極座標変換」をしてみましょう。とはいえいきなり極座標変換はせずになぜ極座標変換をするかの理由を知っておきましょう。
(2)複素数の直交座標と極座標
では,複素数を主に取り扱うことを考えると,通常は式(1)のように表せます。

式(1)がいわゆる複素数でよく出てくる形ですが,これは直交座標(x, y座標)で使う形式です。式を見てもイマイチよくわからんという人のために,端的に伝えましょう。
直交座標のグラフは,主に「変位や移動」を表現できます!
図1に複素数の直交座標のイメージを示します。
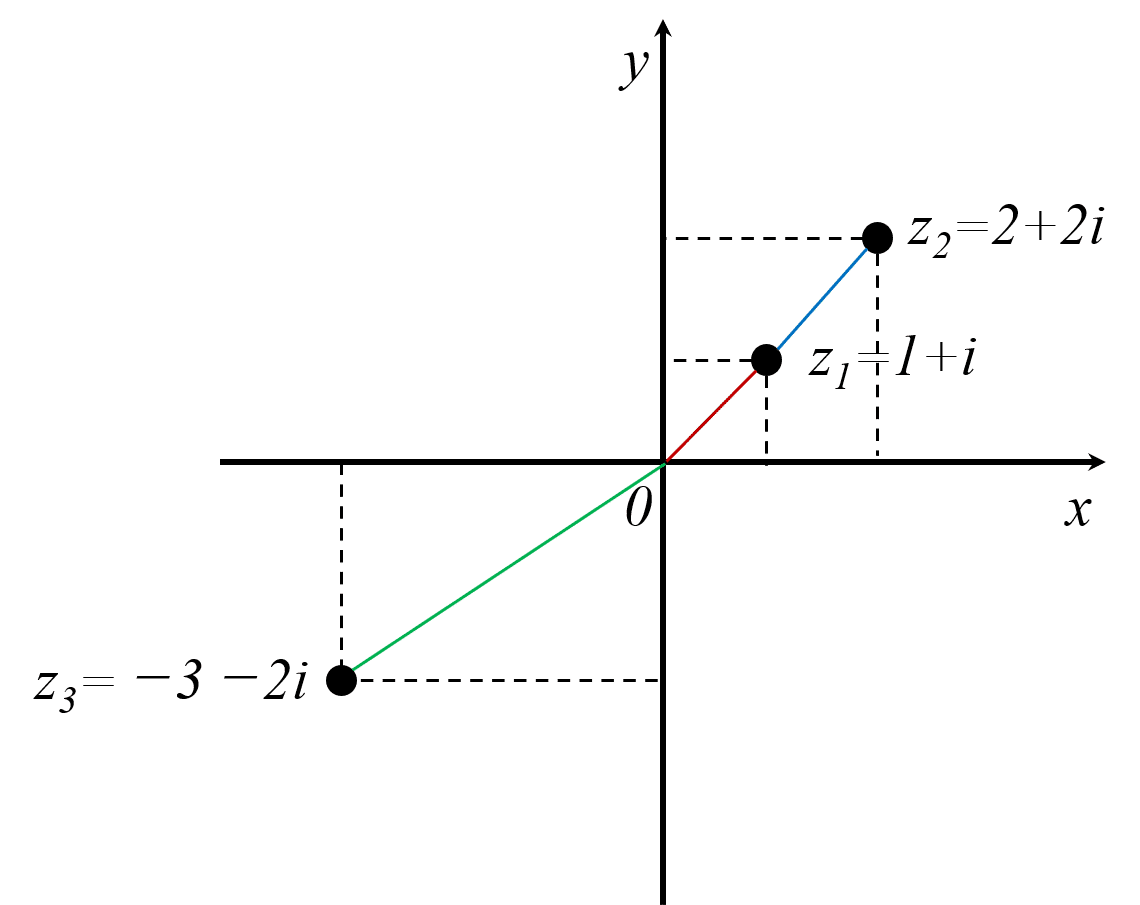
図1 複素数の直交座標
では,複素数を極座標に変換すると,式(1)から式(2)のように表せます。
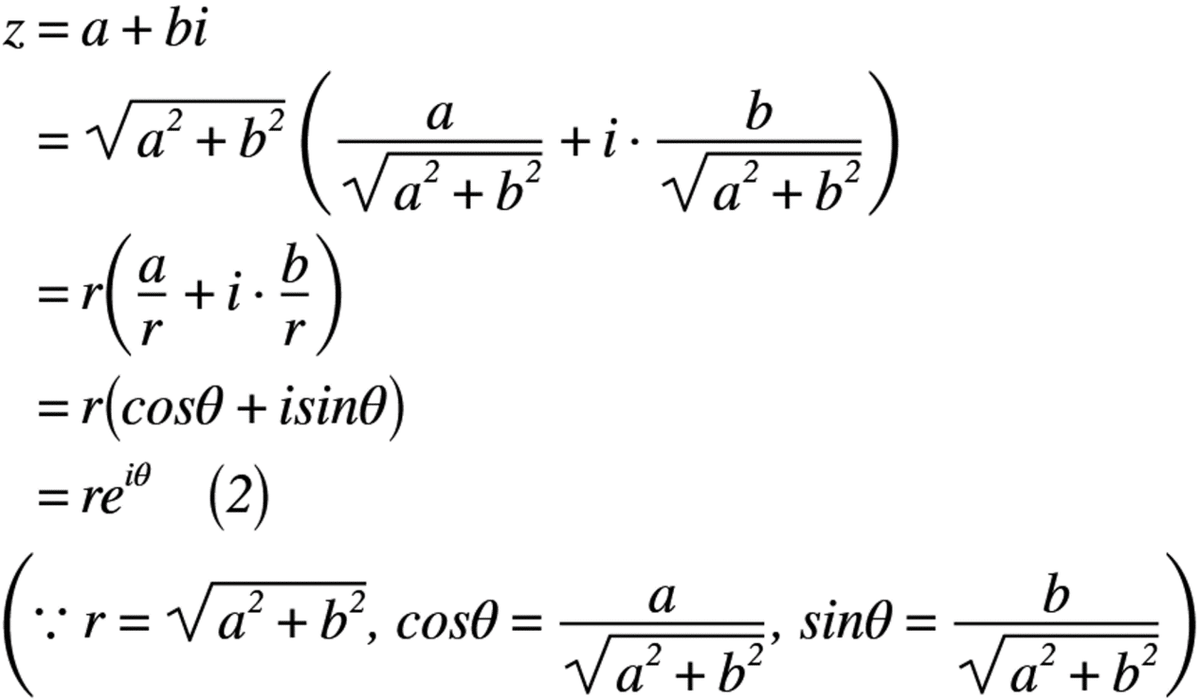
式(2)が複素数の極座標(r, θ座標)で使う形式です。先ほどと同様に,式を見てもイマイチよくわからんという人のために,端的に伝えましょう。
極座標のグラフは,主に「回転」を表現できます。
図2に複素数の極座標のイメージを示します。
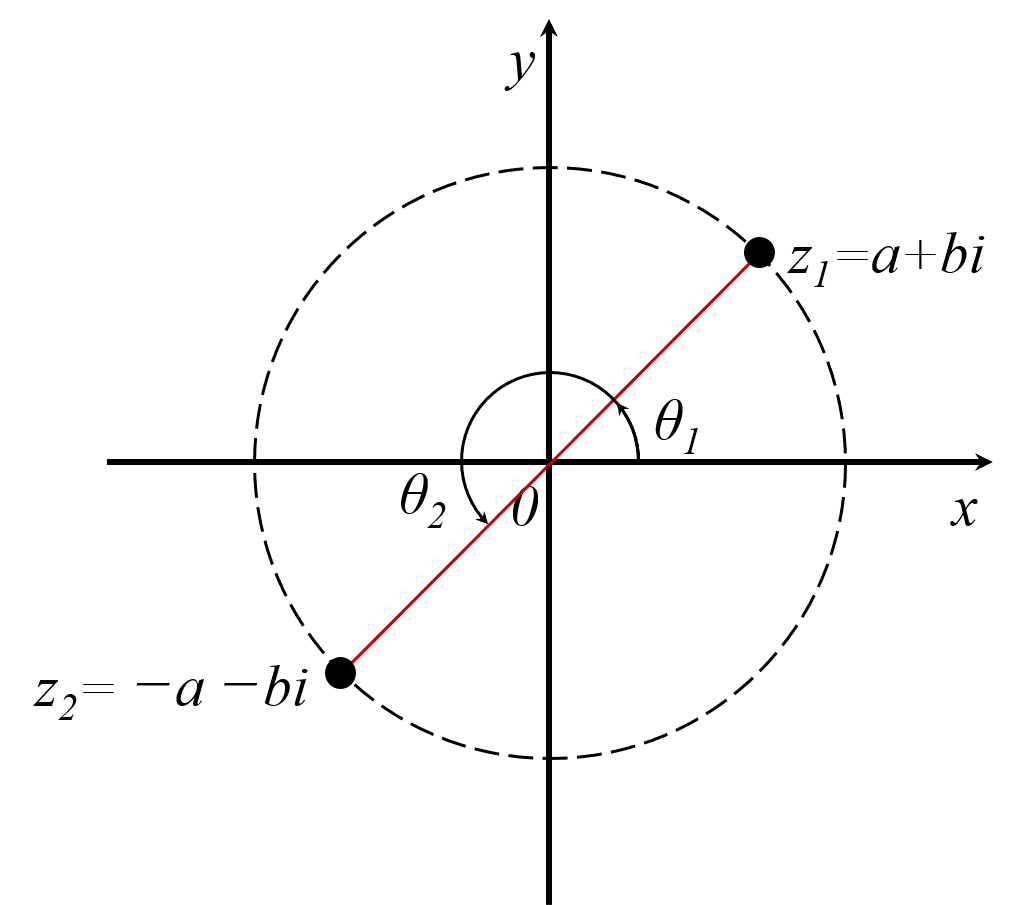
図2 複素数の極座標
よって,直交座標から極座標へ変換することで「回転」を表すことができるようになることが分かりました!
では,C-R微分方程式を使って直交座標から極座標へ変換してみましょう。
(3)C-R微分方程式の極座標変換
早速,C-R微分方程式の極座標変換をするための準備をしましょう。ここで,極座標を考えたときの複素数のx, y方向をそれぞれ考えると,x=rcosθ,y=rsinθとなります。では,与式をr,θについてそれぞれ微分すると,式(3)のように表せます。

では,今度は忘れ去られているであろう速度ポテンシャルφと流れ関数ψをそれぞれr,θをそれぞれ微分すると,式(4)~式(7)のように表せます。




よって,上記の式の下線部が一致していることから,式(4)~式(7)をまとめると,式(8)のように表せます。

これがC-R微分方程式の極座標形式です。見た目上は,ただのx, yからr, θの変換ですが,一部分母にrが掛け算になっているの違いはあります。
(4)複素ポテンシャルの極座標変換
では,複素ポテンシャルの極座標変換をしていきましょう。複素数z(=re^iθ)と実関数w=複素関数w(z)が成立することを前提に考えます。
まず,複素数zをrについて微分すると,式(9)のように表せます。

次に,実関数と複素関数が等しい関係を使い,rについて微分すると,式(10)のように表せます。
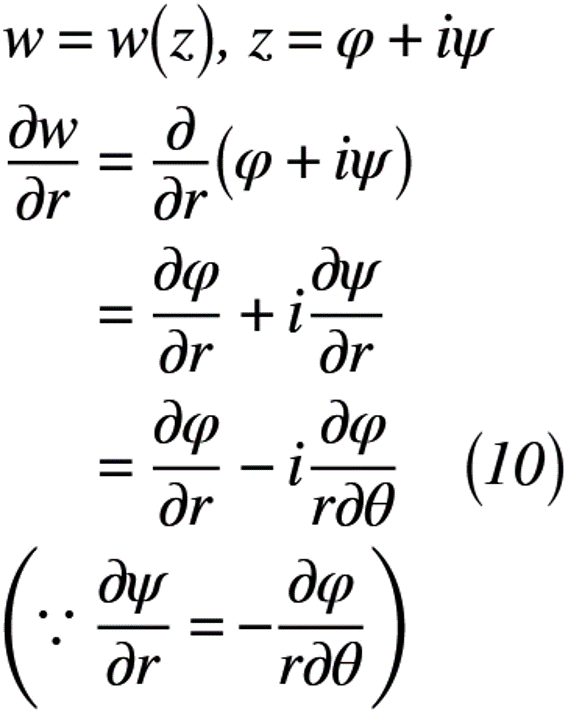
したがって,式(9)と式(10)が等しいことから,式(11)のように表せます。

これによって,以前の記事でかいた複素ポテンシャルの式(6)が導けました。
(5)まとめ
今回の記事のまとめを以下に示します。
(1)複素数の直交座標は「変位や移動」を表すのに対して,複素数の極座標は「回転」を表す。
(2)「C-R微分方程式」及び「複素ポテンシャル」は直交座標から極座標へ変換できる。
以上です。最後まで閲覧頂きありがとうございました。
※次回は,いよいよポテンシャル流れのグラフをちょっとずつ書いていく予定です!
いいなと思ったら応援しよう!

