流体力学　コーシー・リーマンの微分方程式

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第６回目は，第５回目でネタにした「２次元ポテンシャル流れ」で取り扱ったコーシー・リーマンの微分方程式(Cauchy–Riemann equations：以下，C-R方程式と記載する。)について，かいていきたいと思います。かなり数学的な内容になるので，数式が羅列することになることを予めお伝えしておきます。

（１）C-R方程式は何がすごいのか？

　では，「２次元ポテンシャル流れ」で取り扱ったC-R方程式ですが，一体に何がすごいの簡単な復習です。詳しく知りたい方は，以下の記事を見てみてください。

　結論からいえば「連続な偏導関数ならば，とある領域で正則（せいそく）となること」です。言い換えれば，「微分可能であることを使って，流体粒子の運動の様子を複素関数で表現できること」です！
　でも，数学的には，「C-R方程式」が「正則」となることが証明できて，はじめて正しいことが証明でき，かつ利用できるのです。
　ここで，高校数学の「論理と命題」（現在の教育課程では，数学Ⅰ・Aの範囲）を思い出しましょう。先ほど書いたように，「C-R方程式」が「正則」となるためには，早い話「必要十分条件」が証明できればいいのです！図1に「C-R方程式」と「正則」の命題関係を示します。

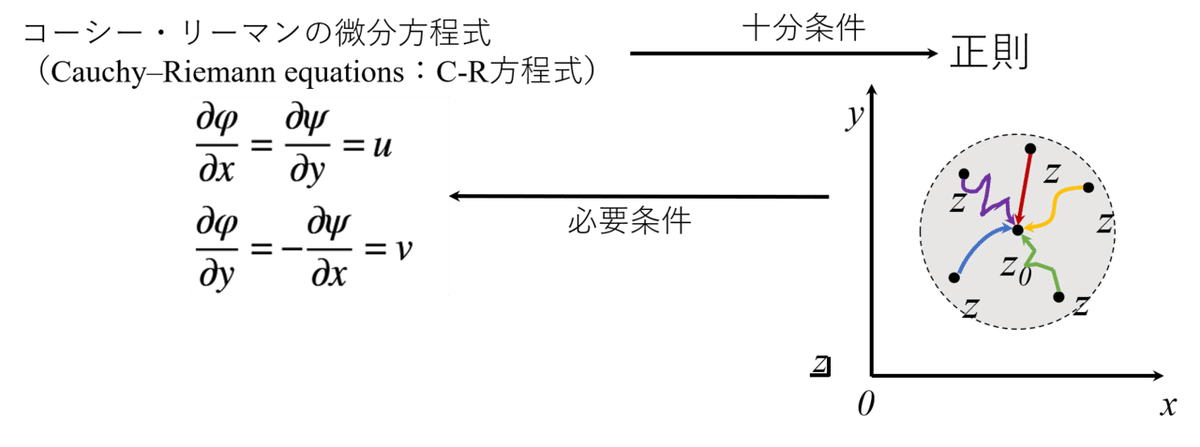
図１　「C-R方程式」と「正則」の命題関係

　なので，「正則」→「C-R方程式」の十分条件と「C-R方程式」→「正則」の必要条件の両方が成立すると，必要十分条件となり，「C-R方程式」が「正則」となることが成立し，「２次元ポテンシャル流れ」に利用できるということです！
　わざわざネタにするぐらいですから，必要十分条件が成立するのですが…。（そもそも，まだわかっていない問題を取り上げるのは，一流の研究者がやるはずですからね。）
　次項では，十分条件と必要条件をそれぞれ証明してみましょう！

（２）「正則」→「C-R方程式」の十分条件

　では，早速ではありますが，十分条件の証明をしてみましょう。タイトルにある「正則」とは，「とある領域で複素関数f(z)が正則である」の意味です。では，これを数式でかいてみると，式（１）のように表せます。

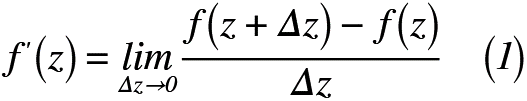
　ここで，ポイントになるのは，複素関数の微分は，関数の傾きを求めることではなく，「とある領域のある任意の点zが点z0に近づく」ことです。図２に任意の点zが点z0に近づくパターンを示します。

図２　任意の点zが点z0に近づくパターン

　図2を見ると明確にわかると思いますが，点zが点z0に近づくパターンは，2種類に分類できるのです。1つ目のパターンは，x方向から近づいていくパターンで，2つ目のパターンは，y方向から近づいていくパターンです。（複雑な動きも結局，この組み合わせで成立するので，本当に2種類だけ考えれば問題なしというわけです。）
　では，x方向から近づいていくパターンを考えてみましょう！

（2-1）x方向から近づいていくパターン

　では，タイトルに記載してあることを数式にしてみる準備をしましょう。複素関数は複素数x+iyで書き表せますが，x方向から近づいていくことを考慮すると，y=0かつx→0になります。でも，実際にはかなり小さい領域での議論なので，Δy=0かつΔx→0となります。
　これを式（１）に適用して書き換えると，式（２）のように表せます。

　よって，x方向から近づいていく複素関数の微分は，複素数で書き表せることが示されました！では，次のステップとしてｙ方向から近づいていくパターンを考えてみましょう！

（2-2）y方向から近づいていくパターン

　同様に，タイトルに記載してあることを数式にしてみる準備をしましょう。y方向から近づいていくことを考慮すると，x=0かつy→0になります。これも先ほどと同様ですが，実際にはかなり小さい領域での議論なので，Δx=0かつΔy→0となります。
　これを式（１）に適用して書き換えると，式（３）のように表せます。

　よって，y方向から近づいていく複素関数の微分は，複素数で書き表せることが示されました！では，式（２）と式（３）を比較すると，式（４）のように表せます。

　式（４）こそ，まさにコーシー・リーマンの微分方程式（C-R方程式）です！
　よって，「とある領域で複素関数f(z)が正則である」→「C-R方程式」の十分条件が証明出来ました！
　次項では，「C-R方程式」→「正則」の必要条件を証明してみましょう！

（３）「C-R方程式」→「正則」の必要条件

　先ほどは図形的（いわゆる幾何学的）に「正則」→「C-R方程式」の十分条件を証明しましたが，今回は微分が使えることを利用します。
　まず，正則であるには，任意の複素関数が「連続」であることが必要です。そのためには，極限が微分したものと同様であることが必要なのです。そこで，微分できることを利用すると，高校数学の微分（現在の教育課程では，数学Ⅲの範囲）で扱う「平均値の定理」が使えます。では，微分可能な１変数関数f(x)の平均値の定理を式（５）に示します。

　ここで，１変数関数f(x)が連続であると，式（６）のように表せます。

　但し，Δx→0のとき，h→0となります。
　式（６）に示したように，１変数関数f(x)では，平均値の定理が成立することを確認できたため，実際に扱っている２変数関数u(x, y)の平均値の定理を式（７）に示すように考えてみましょう。

　但し，Δx→0，Δy→0のとき，h1→0，h2→0となります。
　同様に，２変数関数v(x, y)の平均値の定理を式（８）に示すように考えてみましょう。

　但し，Δx→0，Δy→0のとき，l1→0，l2→0となります。
　よって，複素関数f(z)と複素関数の微分f(z+Δz)をそれぞれ考えると，f(z+Δz)- f(z)は，式（９）のように表せます。

　ここで，式（７）と式（８）を式（９）へ代入すると，式（１０）が表せます。

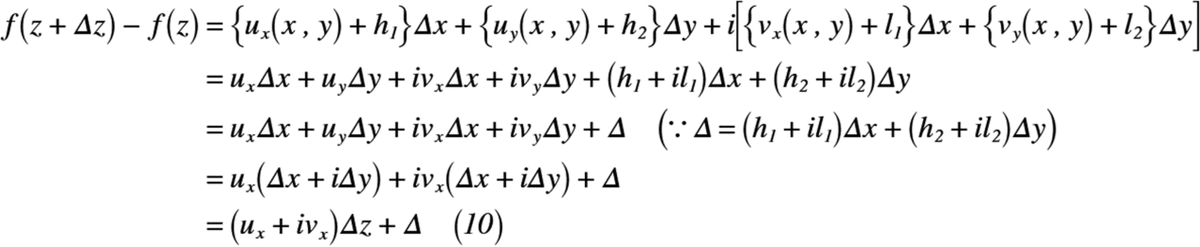
　式（１０）の両辺をΔzで割って，Δz→0の極値を求めると，式（１１）のように表せます。

式（１１）の下線部を考えると，Δz→0から，Δx→0かつΔy→0となるので，式（１２）のように表せます。

　したがって，「２変数関数u(x, y)，v(x, y)が連続な偏導関数で，かつC-R方程式が成立する」とき，「複素関数f(z)はとある領域で正則」となり，必要条件が証明出来ました！

（４）まとめ

　今回の記事のまとめを以下に示します。
（１）「正則」→「C-R方程式」の十分条件と「C-R方程式」→「正則」の必要条件は，両方成立するため，「必要十分条件」となる。

　以上です。最後まで閲覧頂きありがとうございました。