
流体力学 一様流れとわき出しの合成のグラフ
皆様おはこんばんちは。そして,お疲れ様です。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第18回目は,第17回目で予告した通り,「一様流れとわき出しの合成のグラフ」について紹介していきます。
(1)おさらい
さて,今後の記事で取り上げる予定の「一様流れとわき出しの合成のグラフ」についてですが,基になる理論として「一様流れとわき出しの合成」があります。これについては,以前の記事で紹介していますので,知らない方は確認してみてください。
では,「一様流れとわき出しの合成のグラフ」を描いてみます。図1に一様流れとわき出しの合成の概略図を示します。これは勘の良い方なら分かるかもしれませんが,実は「手書き」なのです。概略図なので,あまり問題にならないのですが,実際に描かなければならないときには,このような小手先のテクニックはあまり意味がありません。

図1 一様流れとわき出しの概略図
では,綺麗に描けるようになるには,数式として記述できるのですから,式変形したものを使う必要があるのです。そこで,グラフを描くのに必須となる複素ポテンシャルは,式(1)のように表せます。また,複素ポテンシャルから速度ポテンシャルと流れ関数も式(2)のように表せます。
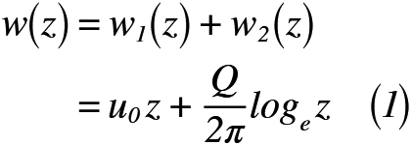

但し,u0は速度,Qはわき出しの強さを示します。
(2)グラフの描画
(2-1)恐ろしいネタバレ
実は,式(2)には速度ポテンシャルと流れ関数を両方示していますが,ここで恐ろしいネタバレをします(以前の「一様流れとわき出しの合成」の記事で気づいた方は素晴らしいです)。
2次元ポテンシャル流れのグラフには,基本的に「流れ関数」しか使わない!
実は,前回の記事でも「流れ関数」が主役になっていて,「速度ポテンシャル」は蚊帳の外だったのです。しかし,速度ポテンシャルは,以前の記事にした通り「渦運動がなくとも流体粒子がもともと速度成分を持っている」かを判別するものに対して,流れ関数は,「時間に対する流体粒子の運動の軌跡」を示したものになります。
結局のところ,流れの様子「だけ」を知りたい場合は,「流れ関数」のみ分かっていればよいのです。よって,今回のグラフの描画には,式(2)の流れ関数のみを使います。
(2-2)重ね合わせの原理を上手く使う
早速,2次元ポテンシャル流れを描くために「流れ関数」を見ていきます。以前の「ポテンシャル流れの合成」の記事で取り扱ったように「重ね合わせ」ができることを解説しました。式(2)の流れ関数をみても「一様流れ」と「わき出し」の2つが合成されています。よって,一様流れの流れ関数をψ1,わき出しの流れ関数をψ2とおくと,式(3)のように分解して考えることが出来ます。すなわち,全く関係のない関数を「足し合わせる」ことができるのなら,上手く「分解」することもできるのです。

2つに分けた流れ関数ですが,以前の「グラフ」の記事と同様に速度ポテンシャルや流れ関数は一定値,すなわち「適当な値を一定の刻み幅で設定できる」のです。そして,グラフに描くためには直交座標である必要があり,半径rやx軸とのなす角θのような極座標で使用するものについては,直交座標で使えるもの変換する必要があります。よって,式(3)は,グラフに描画するには不十分なので,式(4)のような形に式変形する必要があります。

では,式(4)を使って,グラフを描いていきましょう。
(2-3)一様流れのグラフ化
式(4)で示した「一様流れの流れ関数」からグラフ化します。一番簡単なものから手を付けていきましょう。さて,今回の仮定は以下のように設定します。
【仮定】速度u0=0.1cm/s,わき出しの強さQ=2cm^2/s
あとは,流れ関数ψ1とψ2の一定値を設定していきます。今回は,ψ1:-0.9~0.9(0.1刻み),ψ2:0.1~1.9(0.1刻み)としています。表1に式(4)を使った計算結果を示します。
表1 式(4)の計算結果

計算結果は,一様流れとわき出しの両方が記載されていますが,まずは「一様流れの流れ関数」からです。一様流れなので,以前の記事と同様にy軸の値が一定値,すなわちx軸の値の変化を受けないのです。今回も筆者は,表2のようにx軸を-20~20(1刻み)で設定しています。
表2 一様流れのxとyの関係

また,式(4)の結果から一様流れのy値は-9~9(1刻み)となっていることが表1より分かります。これを図示すると,図2のように表せます。

図2 一様流れ
一様流れは実線(赤色)で図示しています。結局,ただ真っすぐな線が描けるだけですが…。
(2-4)わき出しのグラフ化
次に,式(4)で示した「わき出しの流れ関数」をグラフ化します。
わき出しについては,以前の記事と同様にy軸の値がx軸の値によって変化します。今回も筆者は,表2のようにx軸を-20~20(1刻み)で設定しています。表3にxとyの関係表を示します。以前の記事で言い忘れていましたが,x軸の範囲に「マイナス」を含めています。そのため,実際には2π[rad]ではなく,π[rad]だけでよいのです(今回も2πまで計算していますが)。
表3 わき出しのxとyの関係

表3の結果からわき出しを図示すると,図3のように表せます。

図3 わき出し(一様流れを含む)
わき出しは点線(青色)で図示しています。一様流れと重なっていることから少々見辛いことをご了承ください。
(2-5)一様流れとわき出しの交点
最後の山場である「一様流れとわき出しの交点」をつなげる作業です。ここにクセがあるので,初見だとかなり難しいと思います。但し,図1の概略図のようになればよいことが分かっているのですから,そこからヒントを得ましょう。気づくべきポイントは2つです。
1つ目は,一様流れとわき出しの交点から「先端が円形状になる流れ」を描けることです。ここまでは気づく方も多いとは思いますが,問題は「交点の繋げ方」なのです。
2つ目は,「交点の繋げ方」です。ヒントになるのは「重ね合わせの原理」です。流れ関数ψが一定値になることはこれまでも伝えてきた通りですが,一様流れの流れ関数ψ1とわき出しの流れ関数ψ2が存在します。両者は「重ね合わせ」が使えるので,流れ関数ψは両者の変動の影響を受けます。この性質を上手く利用します。
結論としては,「ψ1とψ2の足すことによって,流れ関数ψを表すこと」です。そして,今回の場合は,偶然にもψ=1.0がベースラインになっていたのです。そこから,流れ関数ψを0.5~1,5(0.1刻み)作成しました。表4にその計算結果を示します。
表4 一様流れとわき出しの交点におけるxとyの関係
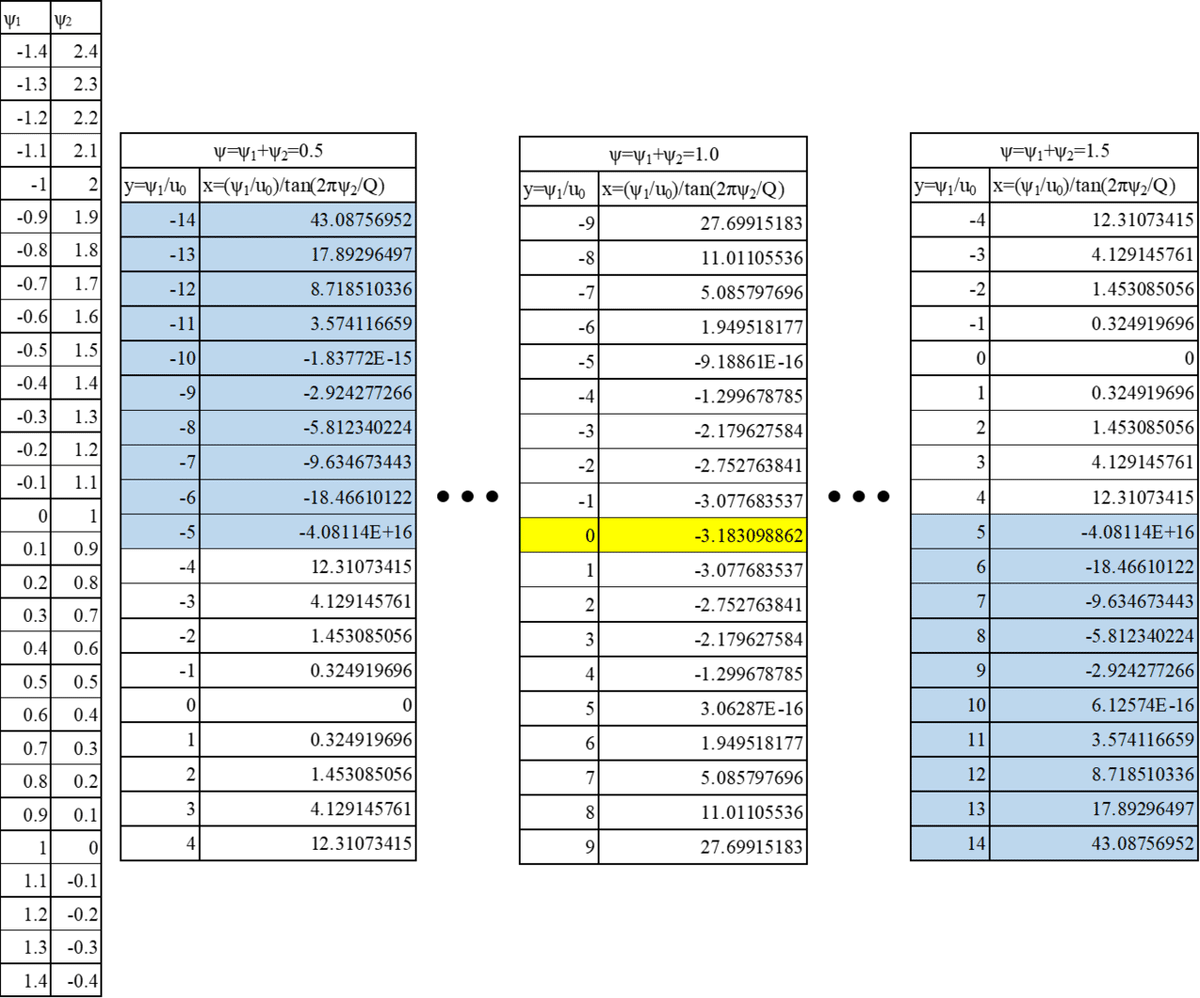
表4を使って,一様流れとわき出しの交点をつないだものを図4及び図5にそれぞれ示します。

図4 一様流れとわき出しの交点
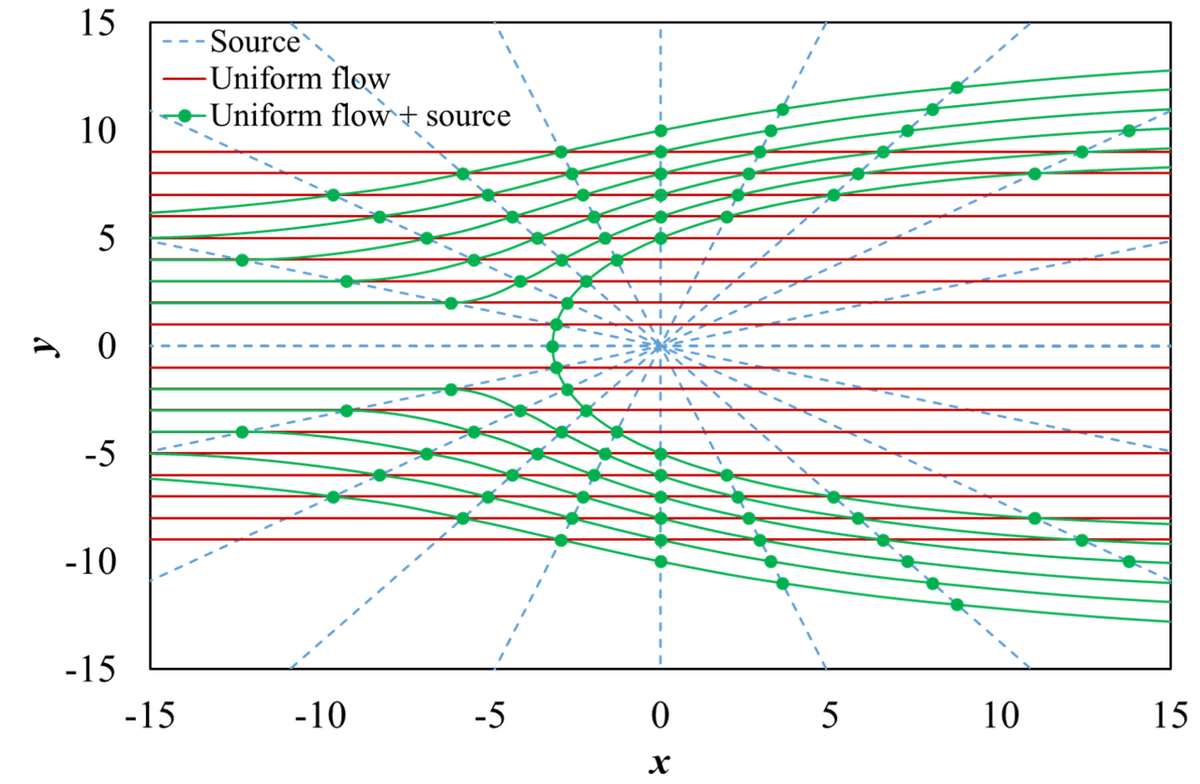
図5 一様流れとわき出しの交点(一様流れとわき出しの線を含む)
一様流れとわき出しの交点は点実線(緑色)で図示しています。実は,表4を作成するときに気を付けないと,図4及び図5のように図示できません。
1つ目は,「よどみ点の座標」を考慮することです。実はψ=ψ1+ψ2=1.0のとき,y=0の場合,本当はx=0となってしまうのです。そのため,先端が本来は引っ込むような図になってしまうのですが,前回の記事で「よどみ点の座標」の算出方法を示しました。これを適用すると,先端が凹むことなく,見事な円形状となるのです。
2つ目は,「単位が2回変化する手前までしか図示しないこと」です。表4でいうとψ=ψ1+ψ2=0.5や1.5がこれに該当します。これで図示すると,途中までしか緩やかな曲線が図示できないのですが,驚きがあります。それは,「途中から一様流れと綺麗に重なること」です。嘘くさいですが,一度やってみると楽しいですよ。
これで一様流れとわき出しの合成図が図示できました。
(3)まとめ
今回の記事のまとめを以下に示します。
(1)一様流れとわき出しの合成図は,一様流れとわき出しの交点で作図できる。
(2)一様流れとわき出しの交点は,一様流れとわき出しの重ね合わせを利用して一定値となるように計算を行う必要がある。
(3)ベースラインを作図するときは,「よどみ点の座標」を考慮する必要がある。
以上です。最後まで閲覧頂きありがとうございました。
※次回は,吸込みとわき出しの合成のグラフについて扱う予定です。
(4)おまけ
どうしてもやってみたかったので,図6に手書きで書いた概略図とExcelで描いた一様流れとわき出しの合成のグラフを比較してみました。

図6 手書きの概略とExcelによる一様流れとわき出しの交点
笑えるくらい違いますね。左の概略図は,筆者のイメージだけで描いたのでいかに実際に描ける流れと違うかが分かりますね。人間が本当に分からないときは,何をしたらよいかもわからなくなるので,こんな手書きでレポートを出して来たら…。恐ろしいですね。笑
いいなと思ったら応援しよう!

