流体力学　わき出しと吸込みの合成

　皆様おはこんばんちは。そして，お疲れ様です。

　最近，流体力学を再度学び直してみようと思い，記事にしています。
　第１９回目は，第１８回目で予告した通り，「わき出しと吸込みの合成」について紹介していきます。

（１）わき出しと吸込みの合成をすると？

　さて，今回の記事で取り上げる予定の「わき出しと吸込みのの合成」についてですが，基になる理論として「ポテンシャル流れの合成」があります。これについては，以前の記事で紹介していますので，知らない方は確認してみてください。

　では，「わき出しと吸込みの合成」を行うと，図１にわき出しと吸込みの合成の概略図を示します。ポテンシャル流れの合成ができると，今までの流れからは想像できない新たな流れ場を図示できるようになります。

図１　わき出しと吸込みの合成の概略図

　図1のような流れ場を描くためには，それに見合った数式が記述できることになります。次項で早速，「わき出しと吸込みの合成」を数式に使っていきましょう。

（２）わき出しと吸込みの合成

（２－１）複素ポテンシャル

　早速，ポテンシャル流れに必須なわき出しと吸込みの「複素ポテンシャル」を求めていきます。以前の「ポテンシャル流れの合成」で取り扱ったように「重ね合わせ」ができることを解説しました。すなわち，全く関係のない関数を「足し合わせる」ことができます。よって，わき出しと吸込みの複素ポテンシャルは，以前の記事で解説しているものを使うと，式（１）のように表せます。

　但し，Qはわき出しの強さ，εは座標の一定値をそれぞれ示します。

（２－２）極座標の変換

　式（１）の対数{}内を確認すると，それぞれわき出しの{}内のz－(－ε)と吹出しの{}内のz－(＋ε)のように表せます。このときの座標を図2のように示します。

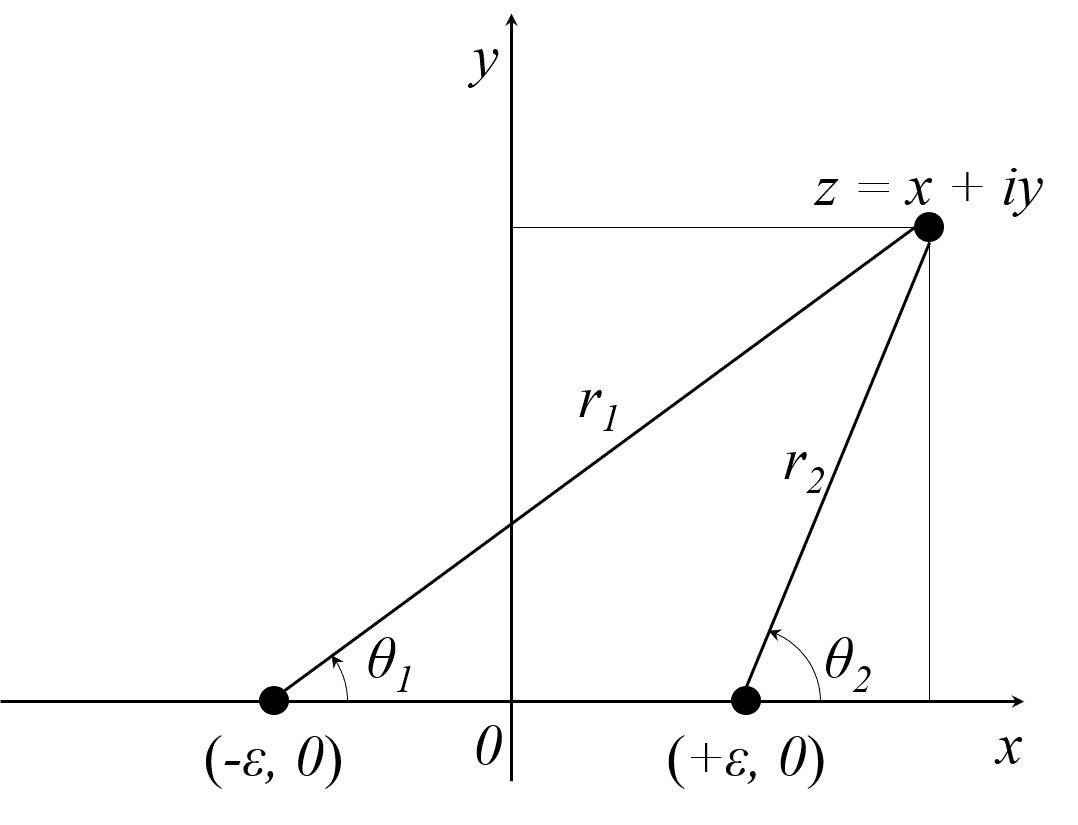
図2　わき出しと吸込みの座標

　図2に従って，複素数zを極座標で表すことが出来れば，式（２）のように表せます。

　このように，わき出しと吸込みの極座標形式に変換可能であることが分かりました。次項では，複素ポテンシャルへ適用した結果を示します。

（２－３）速度ポテンシャルと流れ関数

　式（１）で示した複素ポテンシャルと式（２）の極座標変換式から速度ポテンシャルφと流れ関数ψをそれぞれ考えます。極座標となっている「わき出し」の半径rとx軸とのなす角θの関係式（３）と式（４）は，式（２）を式（１）へ代入した結果です。その計算結果である，式（３）と式（４）は以下のように表せます。また，式（４）は式（３）の比較で確認できる速度ポテンシャルと流れ関数です。

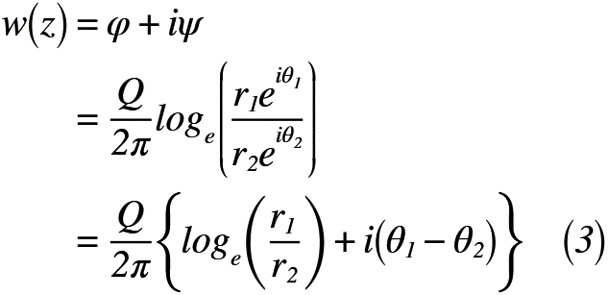
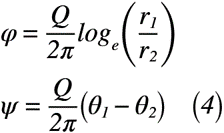
　よって，等ポテンシャル線と流線は式（４）を使って，式（５）のように表せます。

　ちなみに，図1の概略図の破線が「等ポテンシャル線」となり，実線が「流線」となります。次項では，グラフにするための準備へ移ります。

（２－４）流線の半径

では，２－１項～２－３項で今まで分かったものに描き加えたわき出しと吸込みの概略図を図３に示します。

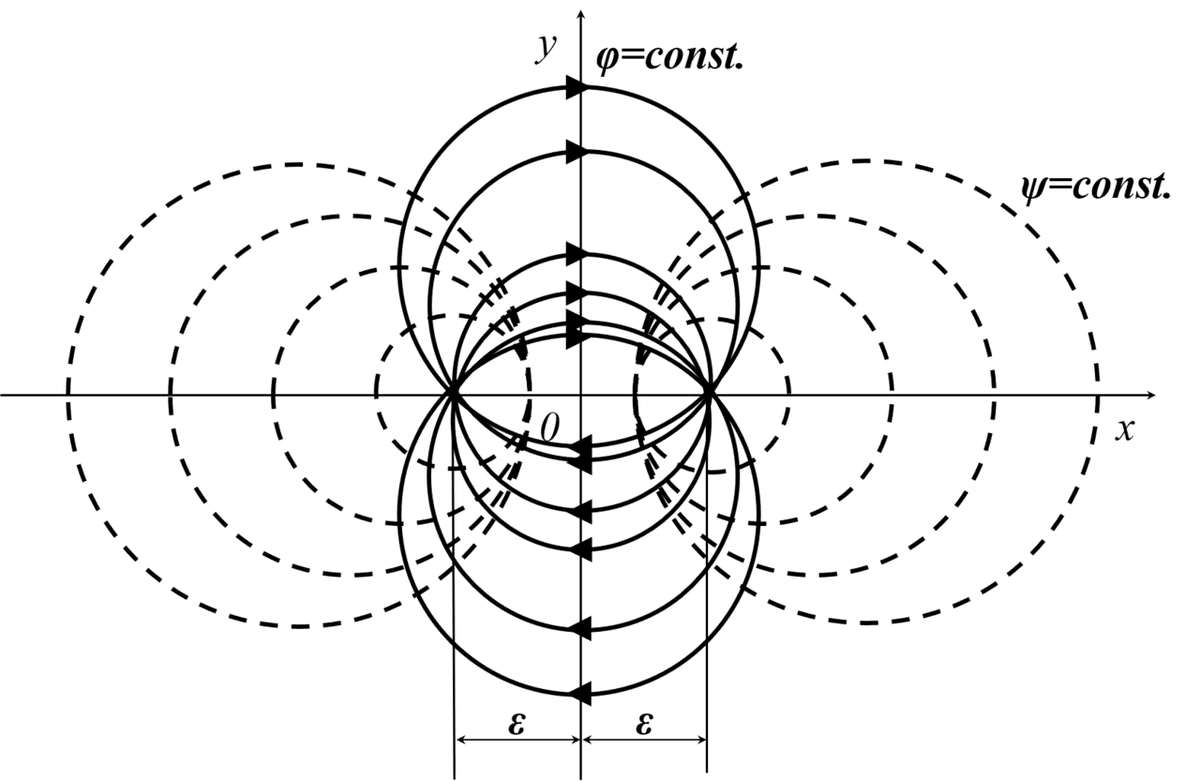
図３　わき出しと吸込みの概略図

　ここで，図３を見ると，とあるx軸の一定値εを原点に同心円状のように広がっていることが分かります（本当は同心円状ではなく，偏心しているのですが…）。厳密にいうと，幾何学では「アポロニウスの円」といいます。そのため，グラフとして描画するためには，等ポテンシャル線と流線の「半径」が必要になります。そこで，まずは「流線」の半径Rψから求めましょう。

　図３のように，y軸上に中心を持つ「流線」の半径を求めるには，円の方程式と幾何学的性質を使ってかくと，式（６）および式（７）のように表せます。

　以上で準備はできました。まず，前項の式（５）の両辺にtan（タンジェント）をとり，加法定理を用いると，式（８）のように表せます。

　次に，式（７）を式（８）へ代入すると，流線の半径Rψの最終結果は，式（９）のように表せます。

　よって，式（９）を使うと，流線を描画できるようになります。

（２－５）等ポテンシャル線の半径

　では，前項と同様に「流線」の半径の次は，「等ポテンシャル線」の半径Rφを求めます。共通して言えるのは，「アポロニウスの円」であることです。そこで，式（１）を式（４）へ代入すると，円の方程式（１０）のように表せます。

　では，さらに式（１０）を整理すると，等ポテンシャル線の半径Rφの最終結果は，式（１１）のように表せます。

　よって，式（１１）を使うと，等ポテンシャル線線を描画できるようになります。今回は，式（９）と式（１１）を使って，グラフの描画をしたいところですが，次回に回したいと思います。そのための準備編とさせていただきます。

（３）まとめ

　今回の記事のまとめを以下に示します。
（１）わき出しと吸込みの合成することで，2つのわき出しと吸込みが存在する。
（２）2つのわき出しと吸込みは，いずれもアポロニウスの円である。
（３）アポロニウスの円の描画に必要な等ポテンシャル線と流線の半径は幾何学的性質から導出可能である。

　以上です。最後まで閲覧頂きありがとうございました。

※次回は，わき出しと吸込みの合成のグラフについて扱う予定です。