
流体力学 シュワルツ・クリストッフェルの定理(その3)
皆様おはこんばんちは。
最近,流体力学を再度学び直してみようと思い,記事にしています。
第54回目は,「シュワルツ・クリストッフェルの定理(その3)」をについて紹介したいと思います。前回,投稿した「シュワルツ・クリストッフェルの定理」と「シュワルツ・クリストッフェルの定理(その2)」の続きとなりますので,気になる方は以前の投稿記事もご確認ください。
(1)問題1
さて,今回はシュバルツ・クリストッフェルの定理(以下,SCの変換式)を使った問題を見てみましょう。では,以下に問題を記載します。
(問)
図1のζ平面に示すように半無限大の長さの帯状領域(幅b)をz平面の上半面に変換する式を求めよ。但し,頂点ζ1,ζ2,ζ3,…に対してx1,x2,x3の3つは任意に選べるものとする。
(解)
まずは,「定理を使うときの注意事項1」の「x1,x2,x3の3つの値は自由に選ぶことができる」を使います。今回は,x1=-∞,x2=-1,x3=1を選択します。
次に,ζ平面上のζ4に対するx4がまだ決まっていないので,値を決定します。ζ平面上のζ4は無限大になるため,ζ4に対するx4は,x4=∞となります。これにより,すべてのζに対するxの値が決まったので,図1のz平面のようになります。

次に,「定理を使うときの注意事項2」の「xi=±∞をとるSCの変換式の項を除く」を使います。そのため,SCの変換式において,ζ平面のζ2,ζ3の内角α2,α3はπ/2となることを使うと,式(1)のように記述できます。

ここで,上式をzについて積分すると,以下のような微分方程式(2)(一般解)が記述できます。このとき,対数関数の微分の関係から積分は以下のように成立します。(過去の記事もご覧ください)


次に,一般解から特殊解の形に持っていきましょう。図1において,定数Bを求めるために境界条件を設定すると,ζ3=0のとき,z3=1(x3=1より)に対応するから式(2)に適用すると,以下のようになります。

次に,図1において,定数Aを求めるために境界条件を設定すると,ζ2=ibのとき,z2=-1(x2=-1より)に対応するから式(2)に適用すると,以下のようになります。
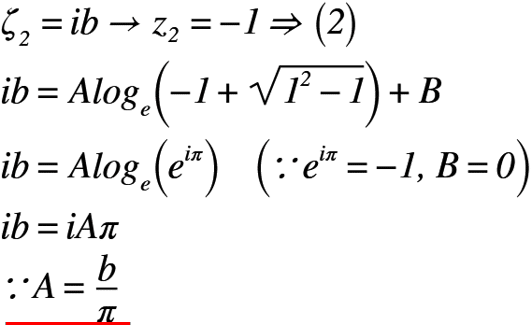
よって,定数AとBの値を求めることができたので,式(2)に代入すると,式(3)のような微分方程式(3)(特殊解)が記述できます。

(2)問題2
(問)
図2のζ平面に示すように半無限大の長さの帯状領域(幅b)をz平面の上半面に変換する式を求めよ。但し,頂点ζ1,ζ2,ζ3,…に対してx1,x2,x3の3つは任意に選べるものとする。
(解)
まずは,「定理を使うときの注意事項1」の「x1,x2,x3の3つの値は自由に選ぶことができる」を使います。今回は,x1=-∞,x2=-0,x3=0を選択します。
次に,ζ平面上のζ4に対するx4がまだ決まっていないので,値を決定します。ζ平面上のζ4は無限大になるため,ζ4に対するx4は,x4=+∞となります。
これにより,すべてのζに対するxの値が決まったので,図2のz平面のようになります。

次に,「定理を使うときの注意事項2」の「xi=±∞をとるSCの変換式の項を除く」を使います。そのため,SCの変換式において,ζ平面のζ2,ζ3の内角α2,α3はπ/2となることを使うと,式(4)のように記述できます。

ここで,上式をzについて積分すると,以下のような微分方程式(5)(一般解)が記述できます。

次に,一般解から特殊解の形に持っていきましょう。図1において,境界条件を設定すると,ζ=ζ1,ζ=ζ4のとき,z=z1,z=z4(いずれも極限を考える)を式(2)に適用すると,以下のようになります。

よって,ζ1-ζ4の値を求めることができました。また,図2のζ平面からζ1-ζ4の値はibであることも分かります。
つまり,両者が同値であることを使うと,式(6)のような微分方程式(6)(特殊解)が記述できます。

式(6)の結果から,式(3)の結果と比較すると,logの中身が多項式から単項式となっています。これは,z平面を見ると直線と原点近くに円ができることによるものと考えられます。その影響で,式(3)を求めるときのように境界条件で各xiの値を指定できないことため,式(6)では積分定数Bが残ってしまうものと推察できます。
(3)まとめ
今回の記事のまとめを以下に示します。
① SCの変換式の注意事項1は,最初に使い,頂点ζ1,ζ2,ζ3に対するx1,x2,x3の値は,3つは自由に選ぶことができる。
② SCの変換式の注意事項2は,SCの変換式のxi=±∞をとるSCの変換式の項を除くことで微分方程式の一般式までたどり着ける。
③ 今回取り上げた問題は,変数分離系の微分方程式となるため,一般解から特殊解を求めることができる。
以上です。最後まで閲覧頂きありがとうございました。
次回は,「翼理論」について,解説する予定です。
いいなと思ったら応援しよう!

