「安定段位は安定しない」の意味

（注意書き）

　今回の記事は「現代麻雀理論」という私が運営していた麻雀研究ブログ（２０１８年２月に閉鎖）で公開した記事の再録である。
　なお、ブログにおける記事の公開日は２０１６年４月。
　約４年前の記事になる。
　また、麻雀のデータを公開する関係で有償にしている。

　なお、この記事の内容は

安定段位７．０近辺における安定段位の標準偏差を予想するもの

である。
　戦術に関連することは全く書いていない。
　よって、戦術目当ての方は買う必要はないだろう。
　記事購入の際の参考にされたい。

　さらに、５月２５日１時、誤植があったのでいくつか訂正している。

はじめに

「安定段位は安定しない」という言葉がある。
　今日はそれについてデータを使いながら考察したい。

　まず、鳳凰卓における安定段位の定義は次のとおりである。

（鳳凰卓安定段位）
　＝　（（６×（トップ率）＋３×（２位率））÷（ラス率））－２

　このように安定段位の計算式にはラス率が分母にある。
　そのため、平均順位と安定段位の関係を綺麗に表すことはできない。

　だが、平均順位と安定段位の関係が分かれば、平均順位の安定性から安定段位の安定性について推測することができる。
　そこで、平均順位２．５近傍における平均順位と安定段位の関係を近似し、平均順位のばらつきから安定段位のばらつきを推測することで、安定段位の安定性を見積もってみようと思う。

平均順位２．５近傍における平均順位と安定段位

　まず、平均順位と安定段位の関係を見積もる際に、一つ仮定を置く。
　それは、「１位率から４位率までは等差数列を採る」という仮定である。
　つまり、平均順位が２．４だったら、１位率２８％、２位率２６％、３位率２４％、ラス率２２％というように、１位率から４位率が等差数列を採るように順位分布を設定するのである。
　そのような条件において、安定段位と平均順位の関係は次のグラフで表される。

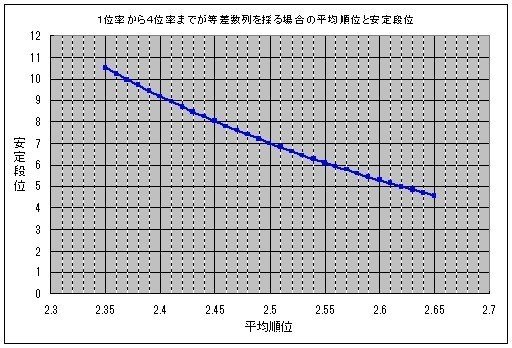
　グラフを荒っぽく見るのであれば、平均順位２．４～２．６においては平均順位が０．０１良くなる（数値的には減る）毎に、安定段位は０．２増える。
　大雑把に見れば、平均順位が２．４だと安定段位は約９、平均順位が２．６だと約５になる。

　これで、平均順位と安定段位の関係は概ね分かった。
　次に、平均順位が打った試合数によってどの程度ばらつくのかを考えてみる。
　
　なお、話を簡単にするため、９５％信頼区間（グラフの数値指標で言えば「５％変動順位」）の上限と平均順位の差をもって、「平均順位のぶれ」と定義する。
（片側検定を行うことも考慮し、一応、９０％信頼区間の数値を１０％変動順位として表しておくが、文章では用いない）。

平均順位のぶれ（２シグマ）

「ｎ試合打ったときの平均順位のぶれ」の求め方は次の通りである。

（平均順位のぶれ）＝１．９６×√（　１．２５　÷（試合数））　

　つまり、平均順位のぶれは標準偏差の１．９６倍と定義する（所謂２シグマ）。
　この場合、試合数と平均順位のぶれの関係は次のグラフ（赤の曲線）の通りである。

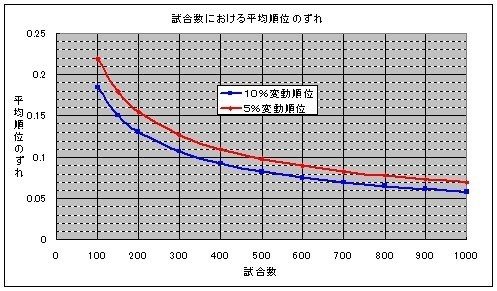
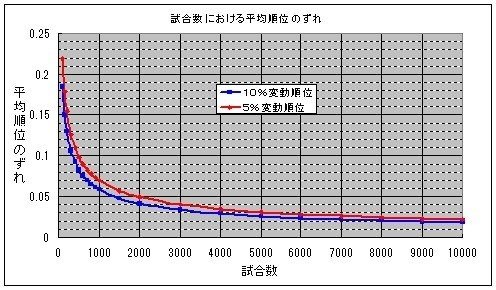
　５００試合における平均順位のぶれは約０．１である。
　２０００試合における平均順位のぶれは約０．０５である。
　８０００試合における平均順位のぶれは約０．０２５である。

　なお、標準偏差で言い換えると、

　５００試合における平均順位の標準偏差は約０．５
　２０００試合における平均順位の標準偏差は約０．０２５
　８０００試合における平均順位の標準偏差は約０．０１２５

となる。

　この点、天鳳の安定ＲＡＴＥ（東風荘のＲＡＴＥではないことに留意）に換算した場合、

５００試合における安定ＲＡＴＥのぶれは約１０６
２０００試合における安定ＲＡＴＥのぶれは約５３
８０００試合における安定ＲＡＴＥのぶれは約２６

になる。

　ちなみに、こちらも標準偏差に置き換えると、

５００試合における安定ＲＡＴＥの標準偏差は約５３
２０００試合における安定ＲＡＴＥの標準偏差は約２６
８０００試合における安定ＲＡＴＥの標準偏差は約１３

となる。

　この点、安定ＲＡＴＥ・平均順位も８０００試合単位で考えれば安定するように見える。
　しかし、２０００試合の場合、安定ＲＡＴＥのぶれは５３、平均順位のブレは０．０５もある。

　これは何を意味するかというと、

平均順位２．５のプレーヤーが２０００試合打つと（９５％の確率で）平均順位２．４５～２．５５の範囲に入る
安定ＲＡＴＥ２０００のプレーヤーが２０００試合打つと（９５％の確率で）安定ＲＡＴＥ１９４７～２０５３の範囲に入る

ということを意味する。

 　つまり、それほど安定しない。
　見かけのＲＡＴＥの平均順位のぶれは約１０６（平均順位約０．１）なので、５００試合以上打てば安定ＲＡＴＥの方が安定する（ぶれない）だけで。


　そもそも、「安定」の比較対象は「見かけ」である。
「見かけＲＡＴＥ」よりも「安定ＲＡＴＥ」の方が安定する、これが「安定」の意味である。
　だから、それ以上の幻想を抱くととんでもないことになる。

安定段位のぶれ・標準偏差

　さて、平均順位・安定ＲＡＴＥのぶれ（標準偏差）について考えたので、安定段位のぶれ（標準偏差）について推測してみよう。

　この点、

（ここから有料となります）