
AI実装検定のサンプル問題をやってみたけど解答がないので自己解説してみる。
AI実装検定の公式で発表されてるサンプル問題を実際にやってみましたが、G検定でも同じことだが解答がないので、勉強しながら解読してみたら、そんなに難しくはなさそうだ。だけど過去問がないので勉強どうしよう・・・。をメモに残しておきました。
AI実装検定とは
AIを100万人が学ぶこと。
それがAI実装検定の設立意義です。
世界の時流においては、流通、エネルギー、金融、軍事、教育、農業、医学、すべての分野でAIの研究が進んでいます。
AI実装検定は中学校までの義務教育を受けていれば誰もが挑戦することができます。
また、理系の方よりは文系の方に、勉強する環境に不自由がない方よりも環境やモチベーションが整っていない方にこそ、是非ともチャレンジしてほしいのです。
AIの難関資格試験「E資格」向けの講座を提供するASAH株式会社は、「AIを100万人が学ぶこと」をミッションとして、AIを実装するスキルを測定する「AI実装検定」を創設、提供を開始したとしています。
AI実装検定レベルの詳細
ディープラーニングの実装について数学、プログラミングの基本的な知識を有し、ディープラーニングの理論的な書籍読みはじめることができ、独学の準備が出来たレベルです。また、現在AI資格試験の最高峰であるE資格(日本ディープラーニング協会主催)の認定プログラムにも挑戦できるレベルです。※プログラムによる。
AI実装検定 試験概要
認定証 ディープラーニング実装士 A級
合格基準 各回毎の基準点(3科目の合計)
科目と配点
・数学:20題
・プログラミング:20題
・ディープラーニング:20題
試験時間:60分(自宅にてオンライン受験)
受験料:3,500円
※シラバスでは、「AI、プログラミング、数学」各20問だが、試験概要での科目名だと、「数学、プログラミング、ディープラーニング」と若干異なる。「ディープラーニング」に該当するのが「AI」なのかも知れない。
試験実績
<第1回 AI実装検定 A級(3/21試験)>
受付開始 :2019年08月15日(木)
受付終了 :2020年03月13日(金)
試験日時 :2020年03月21日(土) 14:00〜15:00
合格発表 :2020年03月30日(月) 予定 (受験9日後)
合格証発行:2020年04月08日(月) 予定
<第2回 AI実装検定 A級(9/26試験)>
受付開始 :2020年03月15日(木)
受付終了 :2020年09月18日(金)
試験日時 :2020年09月26日(土) 14:00〜15:00
合格発表 :2020年10月05日(月) 予定(受験9日後)
合格証発行:2020年10月12日(月) 予定
AI実装検定と同AI試験のレベル分け
下図のように、AI実装検定は、AI最高峰の「E試験」と同様な開発実務向けの試験であるが、レベルを比較的に簡単にしたもの、開発向けエントリー試験という位置づけ。またG検定は企画向けで開発知識は少ないが知識量が幅広くやや難しいとされている。どちらも挑戦したい人にはちょうどいい試験かもしれない。

AI実装検定の合格率
2019年4月に発表された新しい試験で、AI実装検定 第1回試験受験は、2019年7月13日(土)に開催された。なので通算して2020年の第1回は、2回目となる。という感じでまだ新しい試験なので合格率は出ていない。
同種のAIの試験であるG検定、およびE資格はともに70%前後になっている。が数字以上に難しいので合格率はあまりアテにしないほうが良いだろう。
合格したら合格証とロゴが貰える
合格証の発送は、4月8日の予定でしたが、手続きが遅れてるのでもう少し待ってと連絡が来てまして(緊急事態宣言中でしたからね)、実際に届いたのは、 2020/04/14 9:39 でした。メールに直接添付されて以下3点届きました。

〇〇〇〇様
お世話になっております。AI実装検定実行委員会です。
この度は、2020年3月21日(土)開催のAI実装検定 A級 試験を受験頂き、ありがとうございました。
本メールにて、合格証とロゴを添付にてお送りさせていただきます。
名刺などにご使用いただけましたら幸いです。
〜添付データ〜
・合格証
・ロゴ画像2点
ご確認の程、何卒よろしくお願いいたします。
ディープラーニング実装師 合格証
あなたは「AI実装検定 A級」試験に合格し
ここに「ディープラーニング実装師 A級」の称号を授与します。
wwwナニコレ、そんな大そうなモノだっけwww

学習のシラバス
実際に受験してみた結果では、数学問題20問、プログラミング問題20問、AI(ディープラーニング)問題が20問ときっちり順番通りに20問ありました。シラバスでは、「AI→プログラミング→数学」の順ですが、実際は「数学→プログラミング→AI」の順です。(でした)今後は分かりません。
▼ AI 20題
ディープラーニングの基本構造であるニューラルネットワークの基礎的な構造の理解を問います。
・入力層と出力層
・Weight
・順伝播の計算
・行列の掛け算
・バイアス項の導入
・sigmoid関数
・正解値の導入
・二乗和誤差
・誤差の微分
・誤差逆伝播法
・連鎖律
・偏微分
・アダマール積
▼ プログラミング 20題
ディープラーニングの実装においてデファクトスタンダードであるPythonと、数値計算をするための各種ライブラリの実装知識を問います。
・Numpy
・Pandas
・Matplotlib
・Seaborn
・Sciket-learn
▼ 数学 20題
・統計
・関数と微分
・数列と行列
AI実装検定の過去問題と公式テキスト
AI実務検定には過去問題がありません、公式テキストもありません。
公式にも「A級 ~市販の書籍などでも対策可能です~」と書いてあるだけで公式のテキストはないようです。その代わりに「バンビチャレンジ」という名のビデオ学習、もしくはテキスト学習があるようです。
▼ビデオ版(講師解説あり)
お一人様 45,000円(税込)【2020年5月1日 販売開始予定】
▼テキスト版(講師解説なし): お一人様 3,000円(税込) 【期間限定販売中/受験エントリー者のみ購入可】
※テキスト視聴期間は2020年6月30日迄となります。
※実装用ソースコード付きです。
AI実装検定公式テキストの「バンビ・チャレンジ」は小中学生でも親しみやすいテイストですが、進んでいくとAI資格試験の最高峰といわれるE資格の勉強準備が整う、あるいは、基本的なAIの技術書籍が読み進められるほどの高度な内容を習得できます。全国高等専門学校ディープラーニングコンテストに参加する教職の皆様にもご活用いただいている教材です。
▼収録内容
★Bambiβ-Taurus(Section1 基礎編)
Pythonの基礎やパソコンの操作から進めたい方はここからスタート。ニューラルネットに必須な関数の描画や数値計算に必要なライブラリ、NumpyやMatplotlib の扱いも学ぼう。
★Bambiβ-Gemini(Section2 基礎編)
ニューラルネットワークの順伝播の基礎はここからスタート。
★Bambiβ-Cancer1(Section3 応用編)
ニューラルネットワークの逆伝播。ここまで踏み込めば初級者は卒業。
★Bambiβ-Cancer2(Section3 応用編)
ニューラルネットワークの連鎖律。ここが理解できていれば中級者。
★Bambiβ-Leo(Section4 応用編)
中間層を導入した更新式の実装です。ソースコードも配布するので実際に手を動かして「習得」してください。ここが出来ればかなりの実力者です。
★Bambiβ-Virgo1(Section4 応用編)
手書き文字データでディープラーニングを実装します。ここまでできれば中級者は卒業。この先独学でもディープラーニングを学んでいけるレベルに到達することができます。
★Bambiβ-Virgo2(Section5 応用編 ※ここはAI実装検定A級の範囲外です。)
為替データを例に,5つの言語とフレームワークで実装します。(Chainer,NumPy,PyTorch,TensorFlow ,Keras)
為替データはRNNという時系列を扱う概念も登場し、Bambiの世界を超えて上級の域に入ります。
ビデオが、45,000円に対してテキストが3,000円なら、テキストでもよい気がするが、この差はなんだろう。「テキスト視聴期間は2020年6月30日迄」となっているので、ログインして読むタイプのものなのかな、3000円なら買ってもいいかなってお値段なので良いかもしれないです。実際買われた方感想教えてください。
・・・
<サンプル問題を解いてみる>
例題001:AI/入力層と出力層
ニューラルネットワークとは生物の脳の神経回路網を参考に考案された数理モデルである。ニューラルネットワークには「順伝播」と呼ばれる処理がある。下記はこのニューラルネットワークの基本的な構造と順伝播の仕組みについて図示したものである。それぞれの設問に答えよ。
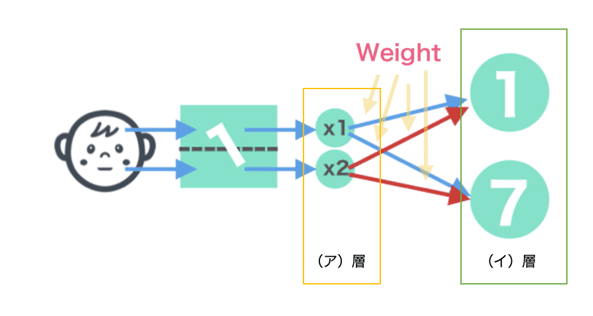
一番最初に情報を受け取るニューロンの集合を(ア)層と呼ぶ。(ア)に当てはまる選択肢は次のうちどれか。
〇 一次
〇 認識
〇 入力
〇 初期
答え:(ア)入力(層)
ニューラルネットワークは、データを受け取る入力層、学習内容に応じてネットワークの状態を変える隠れ層、データを吐き出す出力層の3つの部分で構成されている。ので受け取り口は「入力層」となる。また問題としてはないですが、画像を見る限りは(イ)は出力層となるとみられる
例題002:AI/順伝播の計算
ニューラルネットワークにおける順伝播の処理はPythonなどのプログラミング言語を用いることで比較的簡単に実装することができる。下記は2つのニューロンを用いた順伝播の処理を図示している。それぞれの設問に回答せよ。
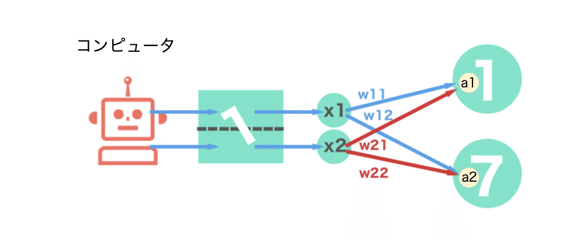
小問1
コンピュータは画像を認識するためには、画像を構成する最小要素「ピクセル」がもつ(ウ)の値を受け取る。(ウ)は各色に対応した0〜255の値をとる。(ウ)に当てはまる選択肢は次のうちどれか。
〇 ソースコード
〇 カラーコード
〇 イメージコード
〇 ユニコード
答え:(ウ)カラーコード
画像は色の点があり、それをドット、もしくはピクセルと呼び、そのひとつのピクセルに色情報が入っているので、ここではカラーコード。
データは画素のRGB値を0~255で表していますが、それを0~1の範囲になるようにスケーリングなどをして利用されます。(ア)、(イ)も本来はあった問題だと推測されるが不明。
小問2
x1 , x2 , Weightが下図に示された値をとるとき、a2の値として正しいものは次のうちどれか。
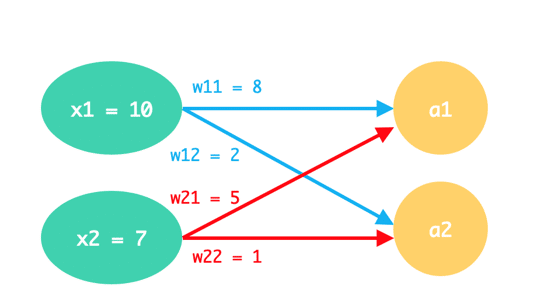
〇 140
〇 27
〇 20
〇 73
答え:27
a1 = x1w11 + x2w21
a2 = x1w12 + x2w12
となるから、a2は
a2 = 10×2 + 7×1
a2 = 27
例題003:AI/行列の掛け算
ニューラルネットワークにおける順伝播の処理は、numpyで表現した行列計算を用いることで実装することができる。下記の図1は順伝播の処理を簡易的に図示したもの、図2は図1の処理をnumpyを用いて行なったものである。それぞれの設問に答えよ。

図2において、(ク)に当てはまる正しい選択肢は次のうちどれか。
〇 2
〇 2.8
〇 8
〇 8.3
答え:(ク)2,8
NumPyを使った全結合層の計算「np.dot」を使うのではないかと思われます(ク)に当てはまるものが、「2.8 」という選択肢がおかしい気がするが誤植なのか、また、設問自体が全部揃っていないので詳細不明。
import numpy as np
x = np.array([[5],[7]])
w = np.array([[2,8],[7,3]])
w.dot(x)例題004:AI/バイアス項の導入
ニューラルネットワークにおける順伝播の処理には伝播された情報の認識精度を向上させる役割の「バイアス項」がある。バイアス項は行列の足し算を用いることで実装することができる。それぞれの設問に答えよ。
下図はバイアス項を含む順伝播の処理を図示したものである。a1の値を求める計算式として正しいものは次のうちどれか。
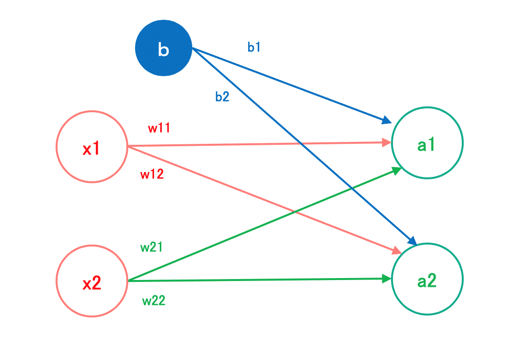
〇 選択肢1 x1 × w11 + x2 × w21 + b1
〇 選択肢2 x1 + w11 + x2 + w21 + b1
〇 選択肢3 ( x1 × w11 + x2 × w21 ) × b1
〇 選択肢4 x1 × w11 + x2 × w21 + b1 × b2
答え:x1 × w11 + x2 × w21 + b1
「バイアス項」は、バイアス項は行列の足し算と書いてある通り、計算上は足し算である必要がある。また順伝播の重みであるw11~w22は掛け算。
例題005:プログラミング/Numpy
ニューラルネットワークでは、各層に重みをかけて次の層の値を求める。各々の計算が大量にあるため、行列を利用することで一度に計算を行っている。Pythonでは、行列の計算は、Numpyというモジュールを利用するが、Numpyについて下記の設問に答えよ
w=numpy.array([[w1,w2],[w3,w4]])、x=numpy.array([[x1],[x2]])とする時、w.dot(x)について正しく述べたものを選べ
選択肢1 w.dot(x)=[[x1*w1+x2*w2],[x3*w1+x4*w2]]
選択肢2 w.dot(x)=[[x1*w1+x2*w1],[x3*w2+x4*w2]]
選択肢3 w.dot(x)=[[x1*w1+x2*w2],[x3*w2+x4*w1]]
選択肢4 w.dot(x)=[[x1*w1,x2*w2],[x3*w1,x4*w2]]
答え:w.dot(x)=[[x1*w1,x2*w2],[x3*w1,x4*w2]](おかしい)
配列の内積は、「左の 1 行目」と「右の 1 列目」の順に計算される。選択肢にw1~4、x1、x2を使った配列の内積なのだが、x3とx4ってどこから来た?
実際に解読してみると下記のような自己解決となった。(wとxを入れ替えると答えが選択し4になった!)
w.dot(x) = np.dot(w,x)
w.dot(x) = w × x
w.dot(x) = [[w1,w2],[w3,w4]] ×[[x1],[x2]]
w.dot(x) = [[w1*x1,w2*x2] , [w3*x1,w4*x2]]
// もしwとxの記号間違いだったとして逆にすると
w.dot(x) = [[x1*w1,x2*w2] , [x3*w1,x4*w2]]
// 選択肢4と一致した!np.dot() は 2 つの引数をとり、それらの行列積を計算して返す関数です。 今、A という行列と 、B という行列があり、行列積 A・B を計算したいとします。 これは np.dot(A, B) と書くことで計算できます。また A.dot(B) と書くこともできます。
// 配列の積内積サンプル
a = ([1,2],[3,4])
b = ([5,6],[7,8])
//np.dot(a, b)
//a.dot(b)
a×b = ( [ 1・5 + 2・7 , 1・6 + 2・8 ] , [ 3・5 + 4・7 , 3・6 + 4・8 ])
a×b = ( [ 5+14 , 6+16 ] , [ 15+28 , 18+36 ])
a×b = ( [ 19 , 22 ] , [ 43 , 54 ])例題006:プログラミング/Numpy
ニューラルネットワークの順伝播では、活性化関数としてシグモイド関数を利用することが多い。シグモイド関数を利用すると、すべての実数を0~1の値に変換するため、確率として表現することが可能となる。Pythonでシグモイド関数を定義した下記の図について以下の設問に答えよ。
シグモイド関数のグラフを選べ

〇 (ア)
〇 (イ)
〇 (ウ)
〇 (エ)
答え: (ウ)
シグモイド曲線は入力した値を0から1の間に収めてくれる関数の1つで、多くの自然界に存在する事柄は、このようなS字曲線を取ります。
解像度が悪くて見にくいが、(ウ)の曲線は、0~1への曲線になっている。
例題007:プログラミング/Pandas
ニューラルネットワークにおいて、直接的な計算はnumpyやscipyで行うのが一般的であるが、Pandasは、データの取り込みや事前のデータ加工あるいは、最終データの出力に利用される。以下Pandasについて設問に答えよ
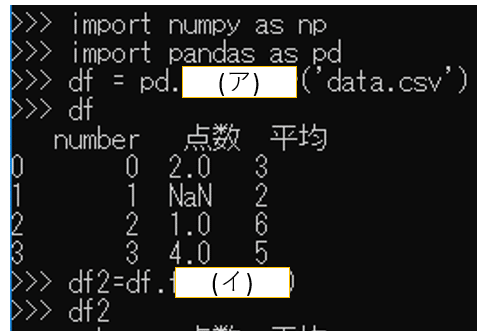
下記図は、CSVからデータを取り込み、加工したのちに、numpyのarrayへと変換を行っているものである。空欄(ア)に当てはまるものを選べ。
〇 read_csv
〇 to_csv
〇 read_txt
〇 to_txt
答え:(ア)read_csv
pandasの関数pd.read_csv()とpd.read_table()はデフォルトの区切り文字が違うだけで中身は同じ。read_csv()は区切り文字がカンマ,でread_table()は区切り文字がタブ\t。
(イ)に関しては虫食いになっているが問題が見えず不明
import numpy as np
import pandas as pd
df = pd.read_csv('data/src/data.csv')
//不明な処理
df2 = df.(イ)
df2例題008:プログラミング/Sciket-learn
Pythonにはたくさんの機械学習モジュールがあるが、その一つがScikit-Learnである。Scikit-Learnは、数値計算ライブラリのNumPyとSciPyとやり取りするよう設計されており、実用面では、Evernoteで利用されている。Scikit-learnについて設問に答えよ
下図は、Scikit-learnを利用して、サポートベクターマシーンによる教師あり学習を行っている図である。(エ)で行っている作業について正しく述べたものを選べ

〇 トレーニングを行っている
〇 trainデータとtestデータに分割している
〇 チューニングを行っている
〇 trainデータとtestデータをそれぞれ加工している
答え:(エ)trainデータとtestデータに分割している
分類するための入力データと、ラベルデータをそれぞれトレーニング用と検証用にデータセットの前方と後方で分割してると思われる。
from sklearn import datasets
from sklearn import svm
digits = datasets.load_digits()
dataset = digits.data
target = digits.target
train_dataset = dataset[:-10]
train_target = target[:-10]
test_dataset = dataset[-10:]
test_target = target[-10:]
clf = svm.SVC(gamma=0.001,C=100.) // SVM 読み込み(ハイパーパラメータ)
clf.fit(train_dataset,train_target) // fitで学習させる
SVC(C=100.0, cathe_size=200, class_weight=None,coef0=0.0,
decision_function_shape="ovr", degree=3, gamma=0.001, kernel="rbf",
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
clf.predict(test_dataset) // predictで予測
array([5,4,8,8,4,9,0,8,9,8])
test_target
array([5,4,8,8,4,9,0,8,9,8])SVM(サポートベクターマシン)は、パーセプトロンに「カーネル関数」と「マージン最大化」を加えて次元を増やすことで、非線形の分割を線形に分割できるようにしているアルゴリズムです。境界に最も近いサンプルとの距離(マージン)が最大となるような超平面で分離する計算をしています。
gammaとCが、調整が必要なハイパーパラメーターで、gammaは、高次元空間へのマップ方法である放射基底関数カーネルで、幅を制御する調整用パラメータ、Cは、正則化パラメーターです。
Scikit-learnにはSVM(サポートベクターマシン)のアルゴリズムが既に実装されているためハイパーパラメーターと学習実行さえ行えば学習ができます。
clf.fit(入力データ, ラベルデータ)と指定することで学習する。今回の問題はこの入力データトラベルデータを用意しているという事になる。
また、Pythonでは、コロンで挟む形で配列をスライスできます。
// Pythonでの配列とスライス構文サンプル
// 文字列の指定
s = 'Python'
s[3]
// 'h' // シーケンスの先頭は、1でなく0
// 配列のスライス(分割)sequence[start:stop]
s = 'Python'
s[2:5] // 先頭から2番目、つまり3,4,5番目の文字が適用
// 'tho'
// 始点、終点の省略が可能
s = 'Python'
s[:5] // 0~5文字目まで
// 'Pytho'例題009:数学/数列と行列
主成分分析とは?多次元データのもつ情報をできるだけ損なわずに低次元空間に情報を縮約する方法!多次元データを2次元・3次元データに縮約できれば、データ全体を視覚化することができる。視覚化によって、データが持つ情報を解釈しやすくなる。
(例:BMIは体重÷(身長)^2という式で表されるが、体重と身長の2つの成分からBMIという1つの成分になる)
次の選択肢の内、当てはまるものを選びなさい。

〇 4,9
〇 5,9
〇 6,9
〇 5,6
答え:意味が分からない(画像の貼り間違えの可能性大)

行列の計算は上記の通り、「左の行列の行間に横線」「右の行列の列間に縦線」を引いて、左側は右へ、右側は下方向に計算を進める。これに当てはめると下記のように計算できます。
例題010:数学/数列と行列
線形変換とは?線形変換とは数学的な意味でベクトルに行列をかけて行列を作る関数のこと!また、線形変換を行うことでベクトルの次元を変更し、ベクトルの回転、拡大・縮小を行う。次元を下げる場合は、元々のベクトルに格納されている成分が冗長な情報を有している、あるいはノイズを含んでいる場合に、それらを取り除く効果が期待できます。次元を上げる場合は、元々のベクトル(データ点)の表現では線形分離ができないが、高次元に埋め込むことで分離できる表現を見つける効果が期待できます。
次の選択肢の内、当てはまるものを選びなさい。

〇 ア:10 イ:22
〇 ア:5 イ:4
〇 ア:-5 イ:-4
〇 ア:3 イ:7
答え:ア:10 イ:22
Ab = [[1x2+2x4] , [3x2+4x4]]
Ab = [[2+8] , [6+16]]
Ab = [[10],[22]]
例題011:数学/数列と行列
ベクトルを使えるとこんなことに繋がる!
コンピュータが言語を扱うときに、単語をベクトル化するWord2Vecという概念があり、これは単語の意味や文法を捉えるために単語をベクトル表現化して次元を圧縮したものである。メリットとしては、単語間の意味に基いて関係性を理解することができるようになる。具体的に言うと、「王様」- 「男」+ 「女」= 「女王」、「パリ」- 「フランス」+ 「日本」= 「東京」といった演算が可能になる。さらに、この手法の延長線としてfacebookよりfasttextという手法が提案された。
次のベクトル計算で、(ア),(イ),(ウ)に当てはまるものを選びなさい。
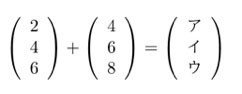
〇 ア:6 イ:10 ウ:14
〇 ア:8 イ:10 ウ:14
〇 ア:8 イ:24 ウ:48
〇 ア:6 イ:24 ウ:48
答え:ア:6 イ:10 ウ:14
行列の足し算は、そのまま同じ位置のも成分どうしを足し算して計算する。
= [[2+4],[4+6],[6+8]]
= [[6],[10],[14]]
試験デモ 第1問/全2問
以下の文章を読み、次の問題に答えよ
ベクトルを使えるとこんなことに繋がる!
コンピュータが言語を扱うときに、単語をベクトル化するWord2Vecという手法があり、これは単語の意味や文法を捉えるために単語をベクトル表現化して次元を圧縮したものである。メリットとしては、単語間の意味に基いて関係性を理解することができるようになる。
具体的に言うと、「王様」- 「男」+ 「女」= 「女王」、「パリ」- 「フランス」+ 「日本」= 「東京」といった演算が可能になる。
さらに、この手法の延長線としてfacebookよりfasttextという手法が提案された。
問題
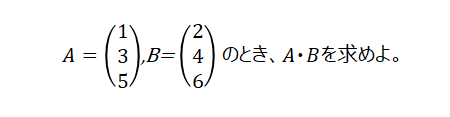
〇 21
〇 25
〇 28
〇 44
答え:44
A・B とは、AとBの行列(ベクトル)の内積の計算
( A , B ) = 1×2 + 3×4 + 5×6
( A , B ) = 2 + 12 + 30
( A , B ) = 44
試験デモ 第2問/全2問
AI実装検定_数学
大門1
ベクトルを使えるとこんなことに繋がる!
コンピュータが言語を扱うときに、単語をベクトル化するWord2Vecという概念があり、これは単語の意味や文法を捉えるために単語をベクトル表現化して次元を圧縮したものである。メリットとしては、単語間の意味に基いて関係性を理解することができるようになる。
具体的に言うと、「王様」- 「男」+ 「女」= 「女王」、「パリ」- 「フランス」+ 「日本」= 「東京」といった演算が可能になる。
さらに、この手法の延長線としてfacebookよりfasttextという手法が提案された。
小問10
次の内積計算で、当てはまるものを選びなさい。
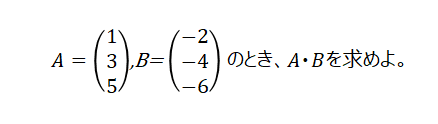
〇 -21
〇 25
〇 28
〇 -44
答え: -44
( A , B ) = 1×(-2) + 3×(-4) + 5×(-6)
( A , B ) = -2 -12 - 30
( A , B ) = -44
行列の積とベクトルの内積について
行列の積の仕方として、基本的な決まり事として、掛け算できる組み合わせがあり、左項の列数と右項の行数が一致している必要があります。また左右が逆になると解が変わる。(AB ≠ BA)
→ベクトルについて
ベクトルの記法を表現するには様々な方法がありますがいずれも同じ、1次元以上のベクトルは行列と呼ばれます。
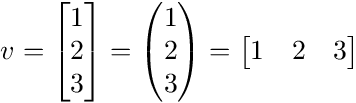
→スカラー演算について
スカラー演算では、ベクトルと数が含まれます。ベクトルの全ての値に対して加算や減算、乗算を行い、ベクトルをインプレースで変化させます。
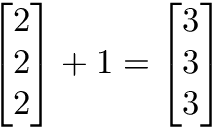
→ベクトルは要素ごとの演算
加算、減算、除算などの要素ごとの演算においては、対応する位置の値を組み合わせて新しいベクトルを求めます。ベクトルAの1つ目の値はベクトルBの1つ目の値と、2つ目の値は2つ目の値といった要領です。つまり、演算が完結するには、ベクトルの次元が一致している必要があります。
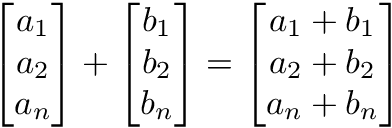
y = np.array([1,2,3])
x = np.array([2,3,4])
y + x = [ 3, 5, 7]
y - x = [ -1, -1, -1]
y / x = [ .5, .67, .75]→ベクトルの乗算
ベクトルの乗算には、内積とアダマール積の2種類があります。
1)ベクトルの内積
2つのベクトルの内積は、1つのスカラーとなります。ベクトルや行列の内積(行列の乗算)は、ディープラーニングにおいて非常に重要な演算です。
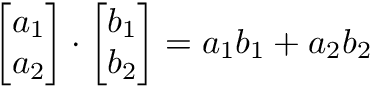
y = np.array([1,2,3])
x = np.array([2,3,4])
np.dot(y,x) = 1*2 + 2*3 + 3*4
np.dot(y,x) = 2 + 6 + 12
np.dot(y,x) = 202)アダマール積
アダマール積は要素ごとの乗算であり、その結果は1つのベクトルとなります。
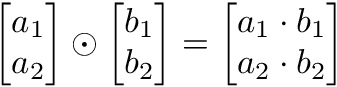
y = np.array([1,2,3])
x = np.array([2,3,4])
y * x = [2, 6, 12]→行列の要素ごとの演算
2つの行列間で加算、減算、除算を行うには、両者の次元が同じである必要があります。
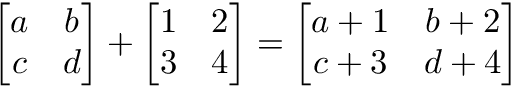
a = np.array([
[1,2],
[3,4]
])
b = np.array([
[1,2],
[3,4]
])
a + b
[[2, 4],
[6, 8]]
a — b
[[0, 0],
[0, 0]]→行列の乗算
・1つ目の行列の列数と2つ目の行列の行数が同じである。
・M×N行列とN×K行列の積はM×K行列である。新しい行列の行数は1つ目の行列の行数、列数は2つ目の行列の列数となる。
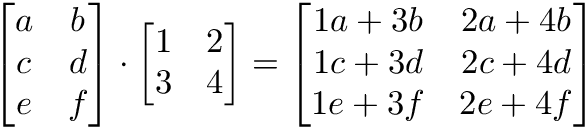
ディープラーニングのための線形代数入門(出典)参照
サンプル問題をやってみて感想
公式にあるサンプルは他のG検定などを見ると、かなり本番に近い問題が出てくると想定されるが、実際に問題を解いてみると、中途半端なところで切り取られた問題なので、私もあまりわからないまま説いてますが、上記回答した通りちょっとおかしいかもしれない。でもこのような問題が出ることは間違いないので、統計学やプログラミングを含めた用語が理解できてPythonでのデータ処理の基本が分かれば解けそうな気もします。
実際の計算などは、60分で60問出てくることを考えても、1問解くのに、何分もかかるものは出てこないと思われる、実際サンプル問題にある計算は暗算で解けるものばかり、とはいえ、暗算より手に書いたほうが早い場合もあるので、メモ帳鉛筆を用意して試験に挑んだほうが良さそうだ。時間かかるものは番号でも控えてあとで再挑戦してもよいと思う。画面にはメモ機能とか後で見直し機能みたいなものがないので(テストセンターでやる試験だとそういう機能があるものもあるので)、時間短縮のためにもリアルなメモ帳もって挑んだほうが良さそう。
また実際にプログラムを書いてみるのも間違いはないでしょうが、原文を模写する時間と、抜粋されてるので、データセットがないなどでそもそもできそうもない、ただ普段Pythonやってればわかりそうな問題ばかりです。
もし間違ってるところやアドバイスなどあればコメントください。
・・・
AI実装検定を受験してみた
・・・
いいなと思ったら応援しよう!

