「教師なし学習」と予測、主成分分析

2023年1月26日 17:58

『データサイエンスのための統計学入門』（オライリー・ジャパン）の第3章「教師なし学習」を参照して、まず「主成分分析」について復習しようと思う。

２変数の例

　「簡単な例」として、元の変数が２つの場合が取りあげられている。１番目の変数は、シェブロン社(CVX)の株価収益(注1)であり、２番目は、エクソンモービル社(XOM)の株価収益である。本に従って、princomp関数を使ってみる。

# A simple example
oil_px <- sp500_px[, c('CVX', 'XOM')]

head(oil_px)　# 2社の株価収益

pca <- princomp(oil_px)
pca$loadings

The principal components for the stock returns for Chevron(CVX) and ExxonMobil(XOM)

　第2主成分について、「CVXとXOMの株価変動を表す」と訳されている。これだとどういうことかわかりにくい。両社の株価の乖離が生じる(diverge)ときにそれが反映される主成分というように正確にとらえるべきであろう。

16変数の例

　以下は、2社ではなく、16社のデータによる分析。データはつぎのようなもの。行はデータの日付、列は会社名。

princomp(top_sp, cor = FALSE)として実行。「cor = FALSE」がデフォルト。

sp_pca <- princomp(top_sp)
sp_pca$loadings

sum((sp_pca$loadings[,1])^2)

上記(負荷量の平方和)を計算すると１になる。

上図左端の151番目と右端の997番目のデータを取り出す。

t(top_sp[c(151,997),])

# 元の変数と主成分得点の相関を計算

sp_pca <- princomp(top_sp)
factor.loadings <- cor(top_sp,sp_pca$scores[,1:4])
round(factor.loadings,digits=3)

sp_pca <- princomp(top_sp)
par(mar=c(6,3,0,0)+.1, las=2)
screeplot(sp_pca, type= "lines",main='')

米国都市の大気汚染

　別のデータでやってみる。Ｂ．エベリット『RとS-PLUSによる多変量解析』（シュプリンガー・ジャパン）の第3章で紹介されているデータ。

princomp()関数を「cor = TRUE」として実行。

usair.dat <- source("data/chap3usair.dat")$value



pairs(usair.dat)
cor(usair.dat[,-1])


dat_s <- usair.dat



model <- princomp(dat_s[,-1],cor = TRUE) # SO2の列を外していいる。


# 結果の出力
summary(model,loading=TRUE)


# 出力ファイルの構造の確認
str(model)

固有値(eigenvalue)の確認

散布図

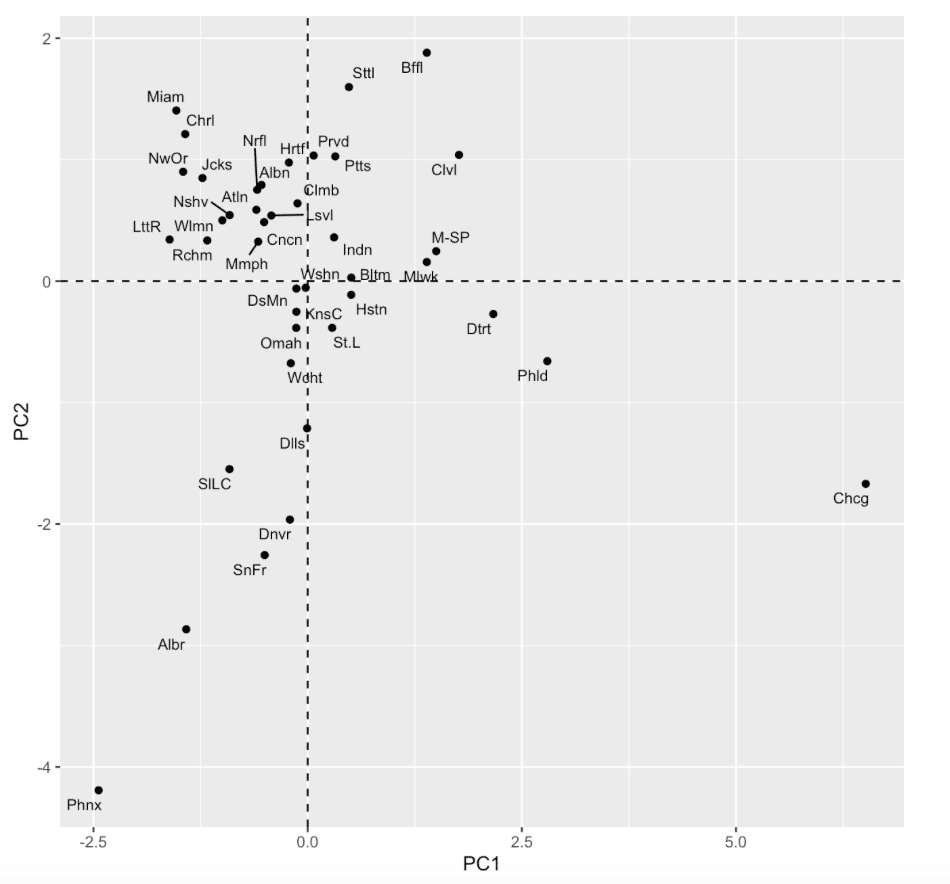
主成分と元の変数との相関関係

factor.loadings <- t(model$sdev * t(model$loadings))[,1:4]

knitr::kable(factor.loadings)

計算にprcomp()関数を使った場合は、以下の通り。上下が反対になっている(注2)。

[注]

(1) 株価収益と訳されているものは、stock price returnsである。これが正確にどういうものなのか私は知らない。
(2) 青木繁伸氏によれば、princomp関数は固有値と固有ベクトルの計算に基づくもので、prcomp関数は特異値分解に基づくものであり、計算精度は後者の方が優れている。青木繁伸『Rによる統計解析』（オーム社）196ｰ197ページ参照。