生存時間分析の基礎１（生存時間分析とは・生存時間分析のデータ形式）

2019年12月7日 13:46

本記事は，生存時間分析の基礎シリーズの第一回目となります．
更新は不定期で著者のきまぐれに左右されてしまいますが，もしよろしければお付き合いください．

先日，生存時間分析モデルの種類の調査を行っていた際に，こちらの記事にであいました．

非常によくまとめてくださっていて，ありがたく拝見させていただきました．紹介されていた数々のモデルの中でも，個人的なニーズと興味から Random Survival Forests (RSF; Ishwaran et al., 2008) を勉強しましたので，そちらに関して紹介していきたいと思っています．

さっそく RSF の解説をといきたいところですが，そちらはすこし後にして，最初は復習も兼ねて，生存時間分析の基礎を確認していきたいと思います．
(上記の Qiita の記事内でも生存時間分析の基礎が丁寧に解説されていますので，そちらを読んでいただいても良いかもしれません)
そして，本記事は，その多くが「エモリー大学クラインバウム教授の生存時間解析（サイエンティスト社）」の内容にもとづいていますので，より詳しく勉強されたい方はそちらを読んでみることを激しくお勧めします！
(余談ですが，この本の原作者であるクラインバウム教授はエモリー大学で長年，公衆衛生の分野で教鞭をとられていた方です．2019 年 12 月現在は引退)
アロハシャツがトレードマークのようですね．

また，この分野では R が Python より充実している印象を個人的にはもっていますので，R を使用して解説をしていきます (といっても，最近は状況が変わっているかもしれません)．
目的の RSF の紹介に辿り着くまで，ある程度の回数を要してしまうと思いますが，気長にお付き合いください．

本記事の流れは以下となります．

1. はじめに

最初に，生存時間分析の概要を説明します．

1 - 1. 生存時間分析とは何か？

生存時間分析とは「あるイベントが起こるまでの時間を説明すべき変数とし，データを解析する一連の統計的手法」です．
例として，下の Figure. 1 のようにくまが蜂蜜を食べるという事象を考えてみます．

このくまは最初の時点で壷いっぱいの蜂蜜をもっていますが，その後時間が経つにつれどんどんと食べていってしまい，最終的には壷を空にしてしまいます．この場合における生存時間分析とは「蜂蜜の壷が空になってしまうというイベント (event) が発生するまでの時間である生存時間 (survival time) を分析すること」を呼びます．
したがって，その名から想像してしまいがちですが，生存時間分析は人などの生物の死亡というイベントだけに関するものではありません．なんらかのイベントが発生するまでの時間を分析するようなものであれば，それも立派な生存時間分析であるといえます．

1 - 2. 用語に関して

以降の説明で使用する用語をここで整理しておきたいと思います．

イベント (event):
死亡，疾病の発症などの特定の個人に起こりうる任意の興味ある事象
生存時間 (survival time):
対象にイベントが起こるまでの時間や打ち切られる（次述）までの時間を呼びます．
打ち切り (censoring):
（ i ）対象にイベントが起こらずに観察期間が終了した場合
（ ii ）観察期間の最中になんらかの理由で対象を観察できなくなってしまった場合（イベントが起きたかどうかも分からない）
（ iii ）興味の対象としているイベント以外の別のイベントが起きてしまいこれ以上観察できなくなってしまった場合
以上の場合は打ち切りと呼ばれる状態です．打ち切られた対象の生存時間はイベントが起きた対象の生存時間とは明確に区別して取り扱うのが生存時間分析の重要なポイントとなります．
右側・左側打ち切り (right/left-censored):
打ち切りが右側か左側，つまり観察期間の右側か左側で発生していることを呼びます．基本的によく見られる打ち切りは下図のような右側の場合です．左側打ち切りは，例えば，観察を始めた時には既にくまが蜂蜜を食べ始めていたような場合想像していただくと良いかもしれません．
区間打ち切り (interval-censored):
真のイベント発生時間が分からない場合，つまり，イベントの発生時点が，ある時間 $${t_1}$$ とある時間 $${t_2}$$ の間にあることは分かっているけれども，その間のどの時点かが分からないような場合のことを呼びます．この生存時間分析の一連の記事ではこのケースを取り扱う予定はありませんが，一応紹介しておきます．

例えば，上の Figure. 2 の場合，くまＡは蜂蜜を食べつくしてしまい，イベント（蜂蜜の壷が空になる事象）が発生していますが，くまＢは大事に蜂蜜を食べていたため，観察期間の終了（Study end）である右端まで蜂蜜の壷が空になっていません（イベントは未発生）．そのため，くまＢに関しては右側打ち切りが発生しています．また，下の Figure. 3 のように，途中でなんらかの理由で観察ができなくなってしまったくま C の場合も，右側打ち切りが発生していることになります．

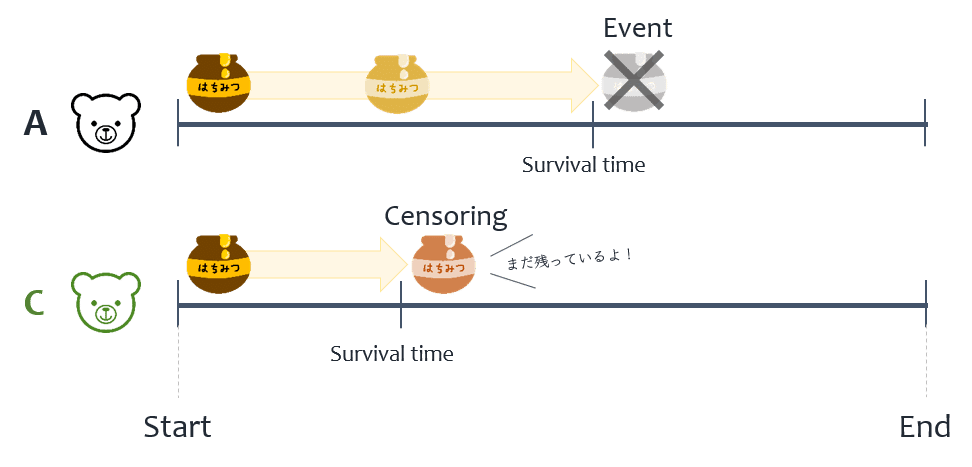
打ち切りに関して，分析上望ましいと考えられる三種類の打ち切りの発生の仕方も紹介しておきます．基本的には，生存時間分析においてはこれらを仮定した上で分析を行っていくことになります．

ランダム打ち切り (Random censoring):
ある時間 $${t}$$ で打ち切られた対象は，同じ時間 $${t}$$ まで生存した全対象の中からランダムで選ばれたと仮定することを呼びます．この仮定に従うと，打ち切られた対象のその後の生存は打ち切られなかった対象のものと同等と考えることができます．

独立打ち切り (Independent censoring):
基本的にはランダム打ち切りと同じですが，全対象の中から「一部の興味のあるサブグループ内で」ランダム打ち切りが成立している場合を呼びます．
全対象内でランダム打ち切りが成立していなくても，各サブグループ内ではランダム打ち切りが成立することがありますので，その場合，独立打ち切りが成立していることになります．サブグループを決める要因として，例えばくまの生息地域などが考えられます．

無情報打ち切り (Non-informative censoring):
「打ち切りの発生が生存時間の情報と無関係でない，もしくはその逆が成立するような状態」を呼びます．
少しイメージがしにくいと思いますので，具体例を考えて見ます．
くま A の友達にくま D がいたとします．くま A はこれまでの例の通り，蜂蜜を観察期間中に食べ終えてしまいます．一方，くま D は観察期間中に蜂蜜を食べ終えることはありません．この時，例えばくま D が蜂蜜を食べ終えたくま A とどこかに一緒に出かけてしまうと，くま D のその後の観察はできなくなってしまいます．このような場合，打ち切り (くま D がいなくなる事象) の発生は生存時間 (くま A が蜂蜜を食べ終えた事象) と無関係ではありません．打ち切りには生存時間の情報がともなうため，無情報打ち切りの仮定は成り立たないことになります．

どれもそれなりに強い仮定ですが，本記事も含め一連の記事で取り扱う生存時間分析はこれらの仮定，特に独立打ち切りの仮定に基づいて行っていくことになります．これらの仮定が成り立たない場合，生存時間の推定に強いバイアスを発生させることがあります．因果推論などを利用した対処の仕方もあると思いますが，そちらは別の機会に譲りたいと思います．

1 - 3. Notation

今後数式を取り扱う際によくでてくる記号をここでまとめておきます．次回の記事以降では，ここで取り上げた記号をあらためて説明することはありませんので，適宜振り返って参照してください．

$${T}$$:　対象の生存時間の確率変数を表します．負でない任意の数値をとります．

$${d}$$:　イベントが起きたか，打ち切りとなったかを表す確率変数で，0 か 1 の値のみをとります．イベントが観察中に起きた場合は 1 となり，イベントが起きずに打ち切りとなった場合や観察期間中に対象が脱落した場合などは 0 の値をとります．

$${Pr(.)}$$:　() の中の状態を実現する確率を表します．例えば $${Pr (T = t) }$$ の場合は，生存時間の確率変数 $${T}$$ の値がある値 $${t}$$ になる確率を表します．同様に，$${Pr(t1 < T < t2)}$$ であれば，生存時間が $${t1}$$ から $${t2}$$ の間である確率を表すことになります．

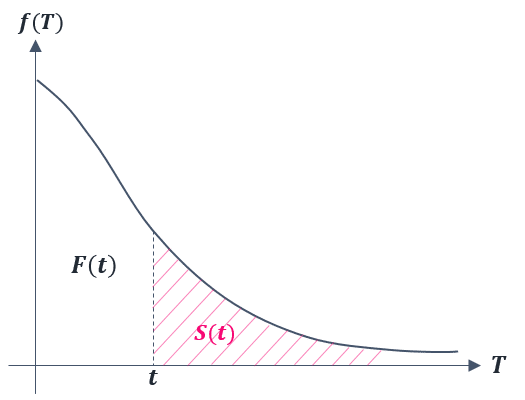
$${f(T)}$$:　生存時間 $${T}$$ の確率分布を表します．確率分布の考え方に関しては，本記事では説明しませんので，分からない方は wiki などを参照してください．下の Figure. 4 の下式のように，確率変数が連続 (continous) である場合と不連続 (discrete) である場合とで表現が異なりますので，その点に注意しましょう．

$${F(t)}$$:　累積分布関数と呼ばれる関数で，下の Figure. 4 の下式のように表すことができます．次に紹介する生存関数とは対の関数となっています．

$${S(t)}$$:　生存関数と呼ばれる関数で，対象がある特定の時間 $${t}$$ よりも長く生存する確率を表します．そのため，$${F(t)}$$ とは対の関係にあり，Figure. 4 の下式の関係にあります．

$${h(t)}$$:　ハザード関数と呼ばれます．「ある対象が時間 $${t}$$ まで生存している条件下」で，単位時間あたりにイベントが起きる瞬間的な可能性をあらわします．少し分かりにくく，あまり馴染みのない関数かもしれませんが，生存時間分析では必須となる関数です．Figure. 4 の下式のように表すことができます．確率を表す式ではありませんので，1 以上の値になる可能性もあります．

$$
\begin{array}{}
f(t) &=& \lim_{{\Delta}t \to 0} \frac{Pr(t < T < t + {\Delta}t)}{\Delta t} \; \; \;(continous) \\ &=& Pr(T=t) \; \; \; (discrete) \\ \\
F(t) &=& \int_{0}^{t} \; f(T) \; dT \; \; \; (continous) \\ &=& \sum^{t}_{T=0} f(T) \; \; \; (discrete) \\ \\ S(t) &=& 1 - F(t) \\ \\
h(t) &=& \lim_{{\Delta}t \to 0} \frac{Pr(t < T < t + {\Delta}t | T \ge t)}{\Delta t} = \frac{f(t)}{S(t)} \; \; \; (continous) \\ &=& Pr(T = t | T \ge t) = \frac{f(t)}{S(t-1)} \; \; \; (discrete)
\end{array}
$$

2. 生存時間分析におけるデータ形式

最初にお話をしたように，今回の記事も含め，今後は R を使用して解説をしていきます．ここでは，R の MASS パッケージ内にある gehan という，白血病患者に対する投薬の効果を調べるために行われた臨床試験のデータを使用します．

2 - 1. 一般的なデータ形式

gehan は生存時間分析の例題としてよく使用されているデータです．
まず，

library(MASS)

data(gehan)
View(gehan)

と実行することで，以下のようにデータの中身をみることができます．

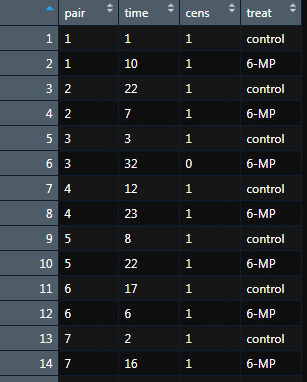
各カラムの説明は以下の通りです．

pair：投薬 (6-メルカプトプリン) 有無の比較のためのペア番号を表す
time：生存時間
cens：打ち切りか否かを表す変数 d に該当
treat：投薬したかどうかを表す (control = 無，6-MP = 有)

このデータを使用して，投薬の有無が生存時間にどのように影響するかを分析するのが主な目的となります．

2 - 2. カウンティングプロセス（Counting Process : CP）形式

上で生存時間分析でよく目にする一般的なデータ形式を紹介しましたが，他にもカウンティングプロセス形式（以下，CP 形式）と呼ばれるデータの形式があります．CP 形式は以下の特徴があります．

1. 1 つの対象が複数行のレコードをもつことができる．つまり，再発イベントなどに対応ができるように，各対象の観察期間が複数の時間区間に分割されている．

2. 各対象の各レコードには，開始時間（start）と終了時間（stop）の 2 つの時間がある．

言葉で説明しても少し分かりにくいと思いますので，実際に 2 - 1 で紹介した gehan データを使って CP 形式のデータを作ってみましょう．
CP 形式のデータを作成するためには，survival パッケージを使用します．このパッケージは R の生存時間分析用のパッケージとしては最も有名なものですので install しておいても損はないでしょう．

install.packages("survival")

# or

library(devtools)
devtools::install_git("therneau/survival")

CP 形式のデータを作成するためには，ユニークなイベントが発生した時間を把握する必要がありますので，以下のようにします．

cut.points <- unique(gehan$time[gehan$cens == 1])
cat(cut.points[order(cut.points)])

# 1 2 3 4 5 6 7 8 10 11 12 13 15 16 17 22 23

全部で 17 種類（1, 2, 3, ..., 17, 22, 23）のイベント発生タイミングがあることが分かりますね．このタイミングの区間で各対象の観察期間が区切られることになります．
あとは，この情報と gehan データと CP 形式の作成に必要なカラム名を survival::survSplit に引数として与えてあげれば，CP 形式のデータを作成することができます．start 引数は，CP 形式作成後の開始時間を表すカラム名を指定しています．ここでは "start" としました．
end 引数には gehan データにおけるイベント発生時や打ち切り時の情報をもつ "time " カラムを，event 引数にはイベント発生の有無を表す "cens" カラムを与えています．

library(survival)

gehan2 <- survSplit(data = gehan, 
                   cut = cut.points,
                   start = "start",
                   end = "time",
                   event = "cens")
colnames(gehan2)[4] <- "stop"
View(gehan2)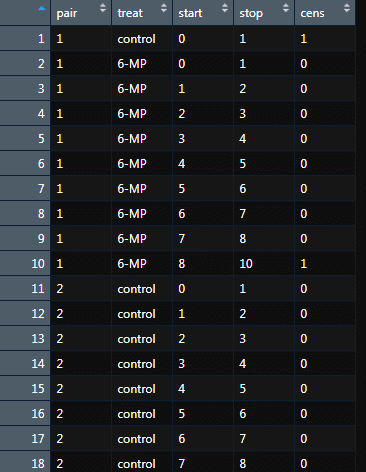

作成された CP 形式のデータの最初の対象（pair = 1，treat = control）をみてみましょう．この対象は，元の gehan データでは，

pair time cens   treat
1    1    1 control

というレコードをもっていました．
time = 1 の時点でイベントが発生し観察が終了した対象であることが分かります．そのため，CP 形式でも，開始時点 0 ，終了時点 1 というレコードを 1 つしかもたないのです．

では，2 番目の対象（pair = 1，treat = 6-MP）はどうでしょうか？
この対象は，元の gehan データでは，

pair time cens treat
1   10    1  6-MP

というレコードをもっています．
time = 10 の時点まで生存し，そこでイベントが発生していますので，
ユニークなイベント発生時点である，1，2，3，4，5，6，7，8 をその観察期間の中に含みます．そのため，CP 形式のデータにおいて 9 つのレコードをもつことになります．

今回は，各対象がイベントを 1 つもしくは 0 しかもたないため，再発イベントのような事象は上のデータの中では確認できませんでしたが，CP 形式のデータのイメージは掴めたのではないでしょうか．

さて，少し長くなってしまいましたが，今回はここで終わりにしたいと思います．
次回は Kaplan-Meier 生存曲線（ログランク検定も余裕がありましたら・・・）を解説したいと思います．
生存時間分析のための導入の説明でこれだけかかっていますので，目的である Random Survival Forests の紹介まで先が長く感じられますが，最後までお付き合いいただければ幸いです．

それではまた次回！

3. Codes

今回使用したコードは以下となります．

4. References

Ishwaran H, Kogalur UB, Blackstone EH, Lauer MS. Random survival forests. The Annals of Applied Statistics 2008;2:841–60. https://doi.org/10.1214/08-AOAS169.