生存時間分析の基礎２（生存曲線と推定生存曲線・Kaplan - Meier 生存曲線）

2019年12月28日 16:24

お久しぶりです．お元気ですか？
本記事の執筆時点（2019 年 12 月末），急激に寒くなり体調を崩しやすい時期となりました．私はといいますと・・・，先日開催された Kaggle Days Tokyo にて，風邪のためマスクをつけて登壇しお話をする羽目になりました．皆様も体調管理にはお気をつけてお過ごしください．
発表内容は私の Speaker Deck にアップしてありますので，ご興味のある方はご覧いただけると嬉しく思います．欠損値の補完（主に多重代入法）に関するお話となります．

さて・・・，今回は前回に引き続き，生存時間分析の基礎を確認していきたいと思います．前回は，生存時間分析の概念，よく使われる用語，notation，分析時のデータの形式などを確認しました．
内容をよく覚えていなかったり読んでいない場合は，下の記事に目を通しておくと良いかもしれません．本記事では，下のリンク先の記事の内容を前提としてお話を進めていきます．

そして，前回も触れましたが，この記事の内容の多くは，「エモリー大学クラインバウム教授の生存時間解析（サイエンティスト社）」にもとづいたものとなっていますので，より詳しく勉強されたい方はそちらを読んでみることをお勧めします．

それでは，次の順で生存曲線とそれに関連した項目を確認していきたいと思います．

1. 生存曲線と推定生存曲線

生存関数 S(t) は下図 4 のピンクの斜線部で表されるように，対象がある特定の時間 t よりも長く生存する確率を表します．前回の記事で，生存時間 T の確率分布である f(T) に対し， t < T の範囲で積分 or 和（確率分布が連続 or 不連続）をとることで，S(t) を計算することができると説明しました．

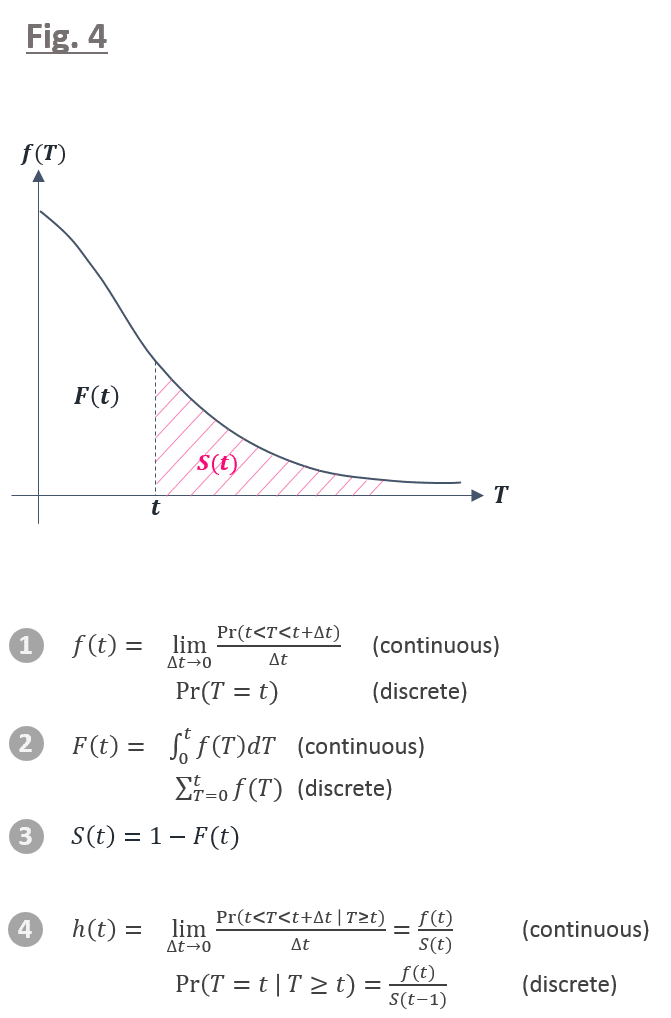
ここで，x 軸に生存時間 t を y 軸に生存関数 S(t) をとりますと，下図 5 のグラフのような曲線を描くことができますが，この曲線を「生存曲線」と呼びます．

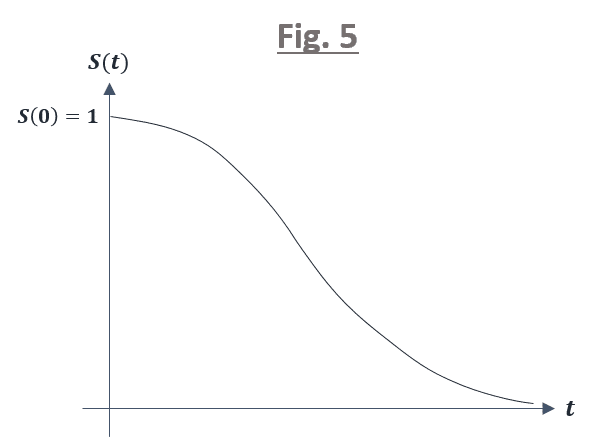
生存曲線は定義から分かる通り，以下の性質をもちます．
（1）S(0) = 1，S(∞) = 0 を満たす
（2）単調減少関数
図 5 のような生存曲線はあくまでも理論的な形状で，有限数の実データから生存曲線を作成すると，下図 6 のようなステップ関数の形となります．

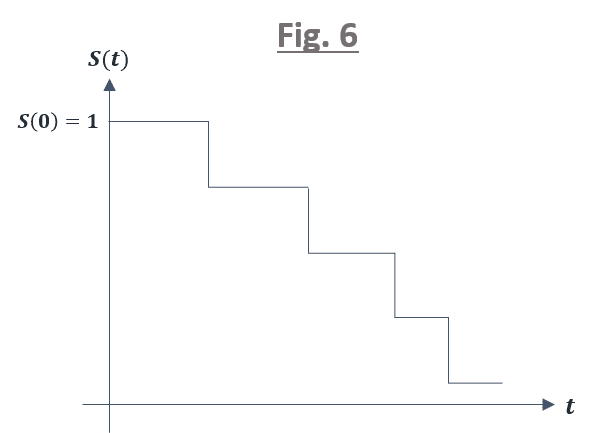
このような生存曲線を「推定生存曲線」と呼びます．推定生存曲線を描くことは生存時間分析の初手であり，非常に重要なプロセスです．

2. Kaplan - Meier 生存曲線

Kaplan - Meier 生存曲線（KM 曲線）は推定生存曲線の中で最も有名でオーソドックスなものです．まずは KM 曲線の作成の仕方を理解しましょう．

ここでは，前回同様に MASS パッケージ内の gehan データを使用して説明をします．また，今回は前回紹介した survival パッケージ以外に survminer パッケージをすぐ後で使用しますので，install しておきましょう．

install.packages("survminer")

# or

library(devtools)
devtools::install_github("kassambara/survminer", build_vignettes = FALSE)

survminer パッケージには，生存時間分析をより行いやすくしてくれる関数がたくさんあります．特に，visualization は美麗で表示可能な情報量も多いです．下はその一例（KM曲線やその信頼区間，各時点での生存数や打ち切り数などを示しています）となります．色々な例とコードが公式ページにありますので，そちらをみてみるのも良いでしょう．

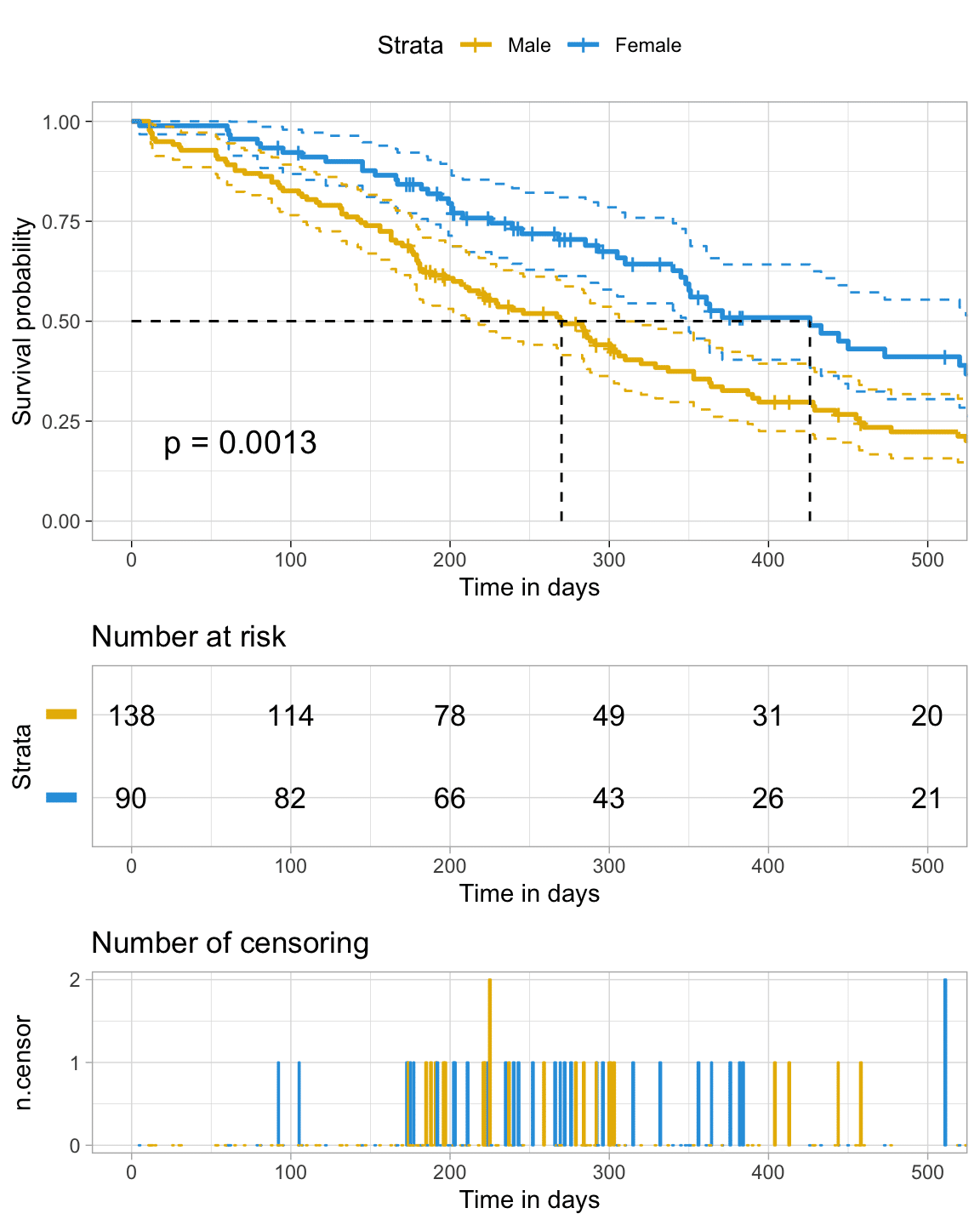
2 - 1. KM 曲線の計算方法

さて・・・，KM 曲線を plot するだけであれば，何も考えずに R のパッケージに頼ってしまうのが一番ですが，本記事では敢えて計算方法の確認もしておきたいと思います．具体的な計算方法を実例をまじえて確認するために，gehan データにおける「昇順に並べた生存時間の表」をみてみることにします．「昇順に並べた生存時間の表」とは，イベントや打ち切りが発生した時点を昇順に並べ，各時点での生存数，イベント発生数，打ち切り数を表形式にしたものになります．言葉よりも見てしまったほうが理解が早いと思いますので，以下のコードを実行してみましょう．

library(MASS)
library(survival)
library(survminer)

＃１
data(gehan)

＃２
surv.obj <- Surv(time = gehan$time, event = gehan$cens)

＃３
ge.sf <- survfit(surv.obj ~ treat, data = gehan)

＃４
ge.sf.df <- surv_summary(ge.sf, data = gehan)
View(ge.sf.df)

コードの流れは以下の通りです．

# 1 : gehan データを load
# 2 : 生存時間分析のための Surv オブジェクトを survival::Surv で作成
# 3 : 作成した Surv オブジェクトを引数とし，survival::survfit で投薬（treat）の有無毎に KM 曲線を作成．ge.sf は survfit クラスのオブジェクトで KM 曲線を表す各種変数（時点，生存数，イベント発生数，生存関数，累積ハザードの標準偏差，生存関数の信頼区間 / 下限 / 上限）を属性としてもつ．
# 4 : 作成した KM 曲線の結果の概要を survminer::surv_summary でデータフレームとして作成

結果，下図 7 のような表（データフレーム）が得られるはずです．

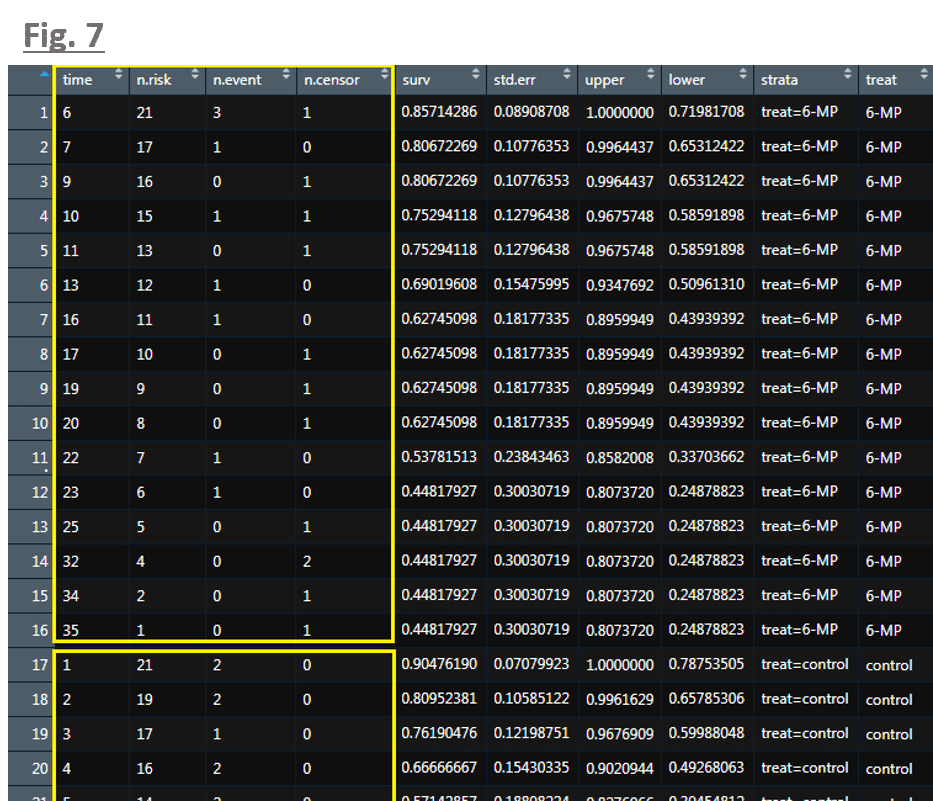
さきほどお話をしました「昇順に並べた生存時間の表」は，上表の中の黄色の枠線で囲った部分となります．黄色の枠線が 2 つあるのは（下側の方は途中で切れていますが），投薬の有無（treat，上図 7 の一番右端にあるカラム）によって分けているからです．
黄色の枠線内の各カラムの意味は以下の通りです．

time : イベントや打ち切りが発生した時点（生存時間）
n.risk : その時点での生存数（リスクセットとも呼ばれます）
n.event : イベント発生数（gehan データの場合は死亡数）
n.censor : 打ち切り数

では，この表を使って，投薬有の群（treat = "6-MP"）における KM 曲線の求め方をみてみましょう．
まず，あるイベントや打ち切りが発生した時点 f における KM 曲線の生存関数 S(t_f) の理論計算式は以下となります．

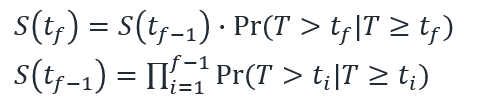
数式の意味するところを少し解釈してみましょう．
1 つめの式は，時点 f の前の時点 f - 1 までの生存関数と Pr( T > t_f | T >= t_f ) との積で表されています．T は生存時間を表す確率変数でした（前回を参照）ので，Pr( T > t_f | T >= t_f ) は「時点 f まで生存していた対象のうち，時点 f より後に生存している対象の割合」を表していると考えることができそうです．同様に考えることで，時点 f - 1 までの生存関数は 2 つめの式のように，各時点 i での「時点 i まで生存していた対象のうち，時点 i より後に生存している対象の割合」を i = 1 から f - 1 まで総乗したものになります．
計算方法は分かりましたので，次は gehan データの投薬有の群（treat = "6-MP"）における KM 曲線の生存関数を計算してみましょう．
下図 8 内の time = 6 時点を f = 1 と考えて，生存関数 S(t_1 = 6) をデータから求めることを考えます．

S(t_0) は，初期時点における生存関数ですので S(t_0) = 1 となります．
Pr( T > t_1 | T >= t_1 ) は，時点 t_1 における生存数が 21 ，時点 t_1 より後の生存数が 21 - 3 = 18 であることから， 18 / 21 = 0.857... となります．
結果，S(t_1) = 0.857... と計算できますが，この値は図 8 におけるピンク色の枠線内の数字（ survival パッケージによる生存関数の計算値）と一致していることが確認できます．同様に時点 t_2 = 7 に対しても計算をしてみると，S(t_1) × 16 / 17 = 0.806... とパッケージで計算されている生存関数と同じ値になっています．無事に，パッケージで計算されている値を再現することができました．
ここで，ひとつだけ注意しておきたいのが，KM 曲線の生存関数の計算においては，ランダム打ち切り（ treat = 6-MP の条件下で今は計算していますので，厳密には独立打ち切り）が仮定されていることです．時点 t_1 の生存関数の計算の際，イベント発生数は 3 であり，時点 t_1 より後の生存数は打ち切られた対象数 1 を含む 18 であるとしました．これは，打ち切られた対象がそれ以降観察はできないものの，時点 t_1 より後に生存している対象と同様の生存パターンであると仮定していることになります．

2 - 2. R における KM 曲線の描画

最後に R での KM 曲線の plot を確認して今回は終わりにしましょう．
KM 曲線は，以下のように survminer パッケージの ggsurvplot 関数を使うことで下図のように描画することができます．

# 5
ggsurvplot(
   fit = ge.sf,
   data = gehan,
   conf.int = T,
   pval = T,
   risk.table = T,
   cumevents = T,
   cumcensor = T,
   ggtheme = ggplot2::theme_light(),
   tables.height = 0.15
)

引数 fit には，先ほど作成した survfit クラスのオブジェクト ge.sf を，引数 data には gehan データを渡しています．
conf.int は信頼区間を描画するかどうか，pval はログランク検定（次回説明します）の p 値を描画するかどうか，risk.table / cumuevents / cumcensor はそれぞれ，各時点での生存数 / 累積イベント数 / 累積打ち止め数を表すテーブルを描画するかどうかを指定しています．他にも，ggplot2 の theme を指定したりなど色々な引数がありますので，気になる方は help や survminer の公式で確認してみると良いでしょう．

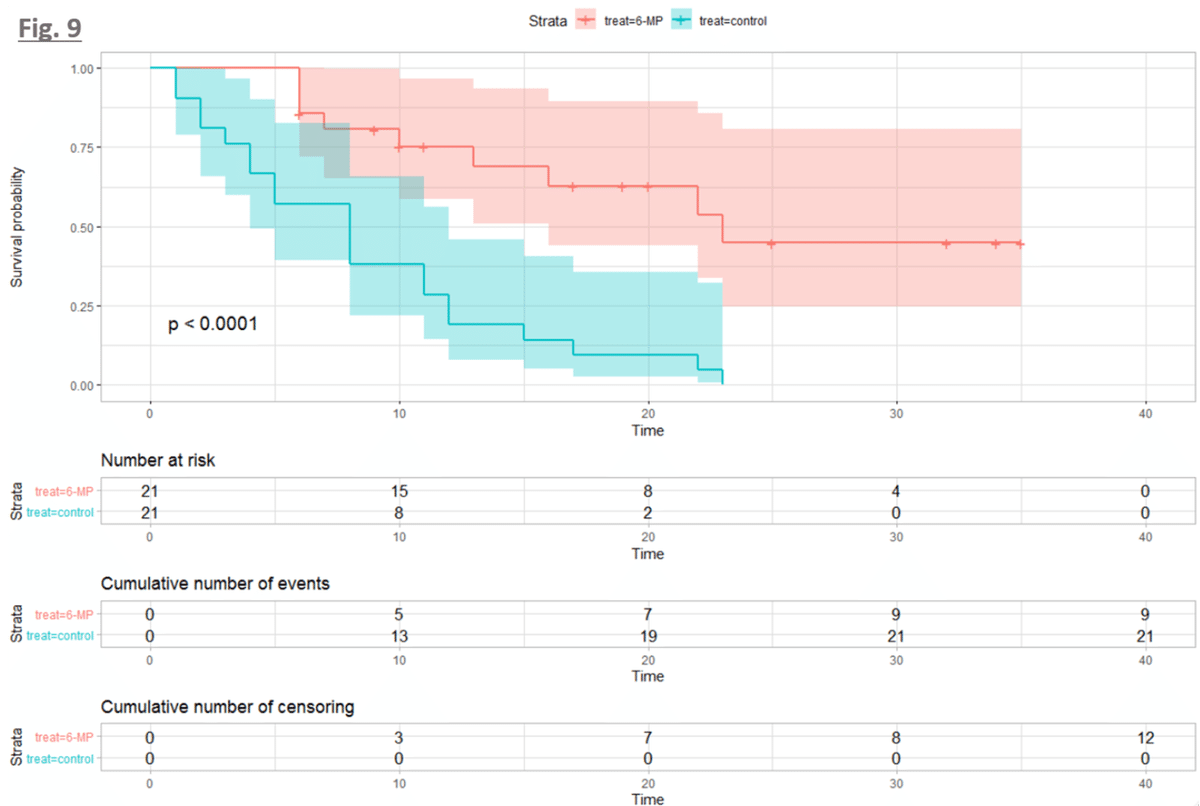
今回は

推定生存曲線の定義
KM 曲線の求め方とその描画の仕方

を確認しました．
次回は「ログランク検定」を解説したいと思います．
それでは，また次回お会いしましょう．

3. Codes

4. Reference

この記事が気に入ったらサポートをしてみませんか？