生存時間分析の基礎 5（比例ハザード仮定の検討 その 1）

生存時間分析の基礎の第 5 回目となります．
なんと・・・前回の記事から二年以上も間が空いてしまいました．
更新が遅くてすみません．
ぼちぼちと再開していきたいと思います．

そういえば，しばらくみないうちに note の仕様が大幅に改良されていますね．Tex 形式で数式が表現できるようになっていて，とても嬉しいです．
内部的には MathJax を使用しているのでしょうか．

さて，今回からは計 3 回に渡って，Cox PH モデルの前提であった「比例ハザード仮定」が成立しているかどうかの検証方法を解説していきたいと思います．
後で復習もしますが，比例ハザード仮定の記事に関しては第 4 回目をご覧ください．

ところで，いきなり話の腰を折るようで申し訳ないのですが，今回から解説する方法を用いて比例ハザード仮定が成り立たないと判断できた場合，当然ながら Cox PH モデルの使用は適切とはいえないことになります．
その場合は，Cox PH モデルではなく別のモデル（拡張 Cox モデルなど）の採用を考えることになりますが，それに関しては今後に譲ります．

また，本シリーズの内容の多くは「エモリー大学クラインバウム教授の生存時間解析（サイエンティスト社）」にもとづいたものとなっていますので，より詳しく勉強されたい方は合わせてそちらを読んでみることもお勧めします．

エモリー大学クラインバウム教授の生存時間解析

それでは，本記事の項目は以下となります．

1. 復習：比例ハザード仮定とは？

まず最初に，比例ハザード仮定の復習をしておきましょう．

比例ハザード仮定とは，ハザード関数 $${h(t, X)}$$ に対して

$$
\begin{array}{}
h(t, X) &=& h_0(t) \cdot \exp({\sum^{p}_{i=1} \beta_i X_i}) \\
\\
h(t, X^*) &=& h_0(t) \cdot \exp({\sum^{p}_{i=1} \beta_i X^{*}_{i}}) \\
\\
\frac{h(t, X)}{h(t, X^*)} &=& \frac{\exp({\sum^{p}_{i=1} \beta_i X_i})}{\exp({\sum^{p}_{i=1} \beta_i X^{*}_{i}})} = constant \; (independent \; of \; time)
\end{array}
$$

が成立することでした．

つまり，
異なる共変量同士（ $${X}$$ , $${X^{*}}$$）のハザード関数の比をとった時，基準ハザード関数 $${h_0(t)}$$ は消えてしまい，「その比は時間 $${t}$$ には依らず共変量のみで決まる」というのが比例ハザード仮定でした．
実際のところ，この仮定は非常に強力な仮定であり，この仮定が成立するかどうかは Cox PH モデルの使用の妥当性を左右します．

以降で解説する比例ハザード仮定の検証方法は，この「時間依存性がない」という考え方を大前提としていますので，その点を頭にしっかりいれておきましょう．

代表的な検証方法には

1.  グラフを使う方法
   

2.  適合度による方法
   

3.  共変量を使う方法

の三種類があります．
本記事では，1 番目のグラフを使う方法を解説していきたいと思います．

2. グラフを使う方法

グラフを使う方法は
グラフから「視覚的に」比例ハザード仮定の検証をする
方法です．

この方法は定性的なものですので，定量的な方法としては，次回以降に解説する適合度や共変量を使った方法の方が良いでしょう．

しかし，それらの方法を使用する前段階としてグラフで検証をしておくと，些細な勘違いやミスの防止などにもつながり，より慎重で丁寧な分析結果が得られる可能性が高くなります．
ですので，グラフを使う方法での検証は決して無駄にはならないといえるでしょう．

さて，グラフを使う方法ですが，
まず最初に
「log-log 生存曲線」
というものを導入します．

第 4 回で Cox PH モデルのハザード関数の定義は以下であることを解説しました（各変数の定義は前記事を参照してください）．

$$
\begin{array}{}
h(t, X) &=& h_0(t) \cdot \exp({\sum^{p}_{i=1} \beta_i X_i}) \\
\\
X &=& (X_1, X_2, …, X_p)
\end{array}
$$

そして，ハザード関数と生存関数は以下の関係式で結びついていることを思い出しましょう．

$$
\begin{array}{}
S(t, X) &=& \exp(- \int^{t}_{0} \; h(u, X) \; du) \\
\end{array}
$$

Cox PH モデルにおけるハザード関数の定義式を上式に代入すれば，生存関数は以下の形に書き直すことができます．

$$
\begin{array}{}
S(t, X) &=& \exp(- \int^{t}_{0} \; h_0(u) \cdot \exp({\sum^{p}_{i=1} \beta_i X_i}) \; du) \\
\\
&=& \bigg[ \exp(- \int^{t}_{0} \; h_0(u) \; du) \bigg] ^{\exp({\sum^{p}_{i=1} \beta_i X_i})} \\
\\
&=& \bigg[ S_0(t) \bigg] ^{\exp({\sum^{p}_{i=1} \beta_i X_i})} \\
\end{array}
$$

ここで，$${S_0(t) = \exp(- \int^{t}_{0} \; h_0(u) \; du)}$$ であり，$${S_0(t)}$$ は共変量 $${X}$$ に依存せず時間 $${t}$$ のみに依存する関数になっています．

さて，先ほど
「log-log 生存曲線」
を導入すると言いましたが，ここで文字通り生存関数に自然対数を二回作用させてみましょう（生存関数は通常は 0 以上 1 以下の値域をとりますので，内側の自然対数の後にマイナス (-) を掛けています）．
すると・・・

$$
\begin{array}{}
\ln \big[ -\ln S(t, X) \big] &=& \ln \bigg[ -\exp({\sum^{p}_{i=1} \beta_i X_i}) \; \ln S_0(t) \bigg] \\
\\
&=& \sum^{p}_{i=1} \beta_i X_i + \ln \big[ - \ln S_0(t) \big]
\end{array}
$$

となりますが，log-log をとったことで，共変量に依存する項と時間に依存する項に分解できていることがわかります．

では，ここで異なる共変量同士（ $${X}$$ , $${X^{*}}$$）の log-log 生存関数の差をみてみましょう．
差を計算してみると・・・

$$
\begin{array}{}
\ln \big[ -\ln S(t, X) \big] - \ln \big[ -\ln S(t, X^{*}) \big] &=& \sum^{p}_{i=1} \beta_i (X_{i} - X^{*}_{i}) \\
\end{array}
$$

となり，時間に依存する項が消えています！
この結果は，
「もし比例ハザード仮定が成り立つのであれば，異なる共変量間の log-log 生存関数の差は，その生存時間に関係なく一定になる」
ということを意味しています．

つまり，異なる共変量の log-log 生存関数（曲線）をプロットして，プロットした生存曲線が互いに平行（一定の差のまま）そうであれば，比例ハザード仮定が成立していそう，ということになります．
そのため，この手法は「グラフを使う方法」といわれているわけです．

では，次のセクションで，survival パッケージ内の cancer データを使用してこのことを確認してみましょう．

3. R によるグラフを使った比例ハザード仮定の検証

cancer データは，North Central Cancer Treatment Group による進行肺癌患者の生存・死亡を記録したものです．

Prospective evaluation of prognostic variables from patient-completed questionnaires. North Central Cancer Treatment Group - PubMed

cancer データは，以下のように 228 人の患者からなるデータで，
病院施設（inst）
年齢（age）
カルノフスキーパフォーマンススコア（ph.karno）
などの 10 変数があります．

> glimpse(survival::cancer)
Rows: 228
Columns: 10
$ inst      <dbl> 3, 3, 3, 5, 1, 12, 7, 11, 1, 7, 6, 16, 11, 21, 12, 1, 22, 16, 1, 21, 11, 6~
$ time      <dbl> 306, 455, 1010, 210, 883, 1022, 310, 361, 218, 166, 170, 654, 728, 71, 567~
$ status    <dbl> 2, 2, 1, 2, 2, 1, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,~
$ age       <dbl> 74, 68, 56, 57, 60, 74, 68, 71, 53, 61, 57, 68, 68, 60, 57, 67, 70, 63, 56~
$ sex       <dbl> 1, 1, 1, 1, 1, 1, 2, 2, 1, 1, 1, 2, 2, 1, 1, 1, 1, 1, 2, 1, 1, 2, 1, 1, 1,~
$ ph.ecog   <dbl> 1, 0, 0, 1, 0, 1, 2, 2, 1, 2, 1, 2, 1, NA, 1, 1, 1, 2, 2, 1, 1, 0, 1, 0, 0~
$ ph.karno  <dbl> 90, 90, 90, 90, 100, 50, 70, 60, 70, 70, 80, 70, 90, 60, 80, 80, 90, 50, 6~
$ pat.karno <dbl> 100, 90, 90, 60, 90, 80, 60, 80, 80, 70, 80, 70, 90, 70, 70, 90, 100, 70, ~
$ meal.cal  <dbl> 1175, 1225, NA, 1150, NA, 513, 384, 538, 825, 271, 1025, NA, NA, 1225, 260~
$ wt.loss   <dbl> NA, 15, 15, 11, 0, 0, 10, 1, 16, 34, 27, 23, 5, 32, 60, 15, -5, 22, 10, NA~

今回は簡単のために，
time: 生存時間を表す
status: 右打ち切りの有無を表す（1: 打ち切り; 2: 死亡）
sex: 性別（1: Male; 2: Female）
ph.ecog: ECOG パフォーマンスと呼ばれるもので，患者の日常生活の制限の程度を表す（0 - 4: 数字が大きい程自由がきかなく，4 だとほぼ寝たきり状態を表す）
の 4 変数を使用して比例ハザード仮定の検証をしてみましょう．

まず，検証用にデータを適当に加工します．

cancer <- survival::cancer %>% 
    filter(!is.na(ph.ecog) & ph.ecog < 2) %>% 
    mutate(
        status = ifelse(status == 1, yes = 0, no = 1), 
        sex = factor(sex, levels = c(1, 2), labels = c("M", "F")), 
        ph.ecog = as.factor(ph.ecog)
    )

上では，検証を行いやすくするため
ph.ecog 変数が 0 か 1 の患者のみを抽出し，survival::Surv 関数の event 引数用に status 変数を 0/1 に変換し，sex と ph.ecog 変数を因子型（カテゴリ型）に変換しています．

データの準備ができましたので，比例ハザード仮定を検証してみましょう．log-log 生存曲線は，生存関数に対し log-log 演算を施すことで描くものでした．そのため，生存関数が必要ですが，それには推定生存曲線である Kaplan - Meire 生存曲線（KM 曲線）を利用します．
その点で，log-log 生存曲線は「log-log KM 曲線」とも呼ばれたりします．
KM 曲線を忘れてしまった方は第 2 回の記事を振り返ってみてください．

まずは，Surv オブジェクトを survival::Surv 関数で作成し，作成した Surv オブジェクトを引数とし，survival::survfit 関数で性別（sex）に KM 曲線を作成します．

surv.obj <- Surv(time = cancer$time, event = cancer$status, type = "right")
sf.obj <- survfit(surv.obj ~ sex, data = cancer)

作成した sf.obj は log-log 曲線の描画に必要な以下の arguments をもっています．
time: 各プロットに対応する生存時間
surv: 生存関数の値
strata: 層化別のプロット点数（今回の場合は Men: 96; Women: 69 となっている）

生存関数の値 surv に対して log-log 演算を施してあげた後，ggplot で描画してあげると以下の figure. 1 を得ることができます．具体的な code は https://github.com/Greenwind1/survival-analysis/blob/3b7111b7a4bd484d292495d658fc997e8ed99f6d/src/note_05.R#L34 を参照してみてください（少し冗長な code です）．

Figure. 1

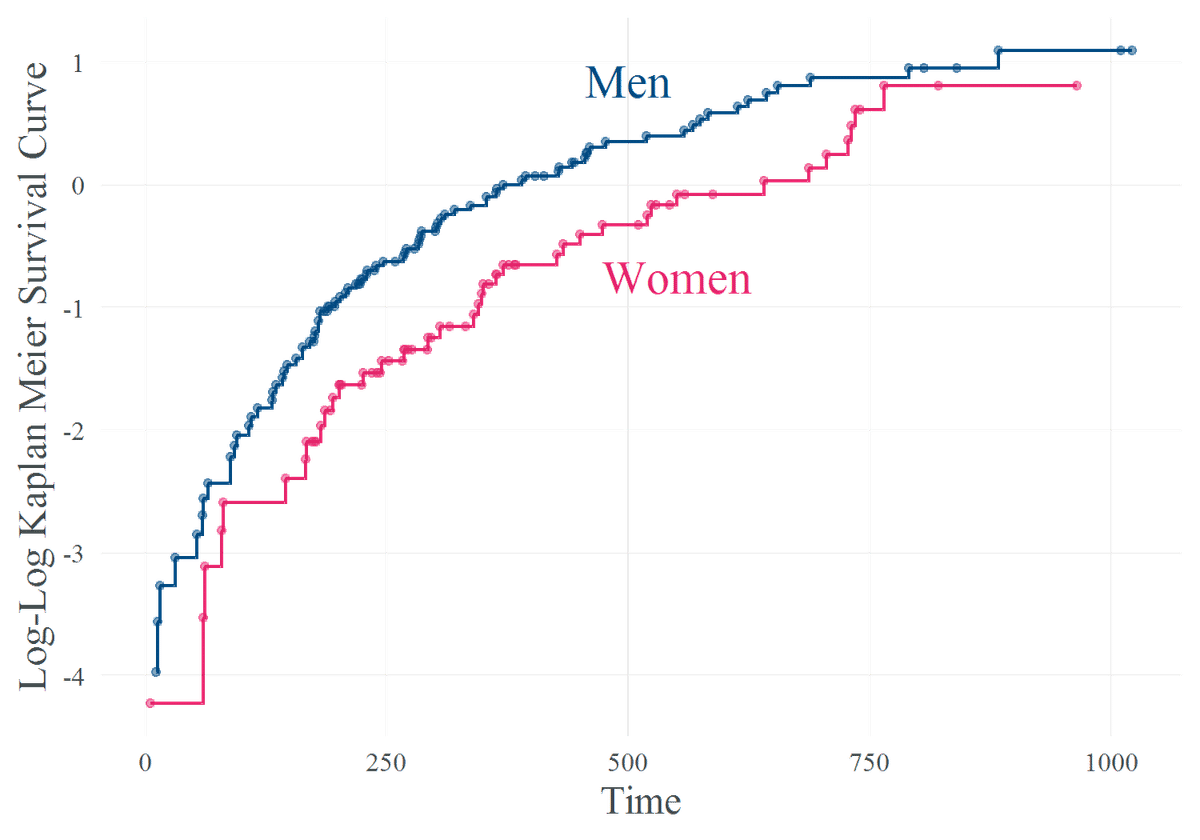
得られた上図（Figure. 1）をみてみると・・・
なんとなくですが，性別を共変量とする場合は比例ハザード仮定が成立していそうです（雰囲気大事）．全生存時間に渡って完全に平行ではありませんが，少なくとも男性と女性の生存曲線が交差するようなことは起きていないことがみてとれます．

では，今度は ECOG performance 別に KM 曲線を作成し，それを元に log-log 生存曲線を描画してみましょう．手順は先ほどと全く同じです．

surv.obj <- Surv(time = cancer$time, event = cancer$status, type = "right")
sf.obj <- survfit(surv.obj ~ ph.ecog, data = cancer)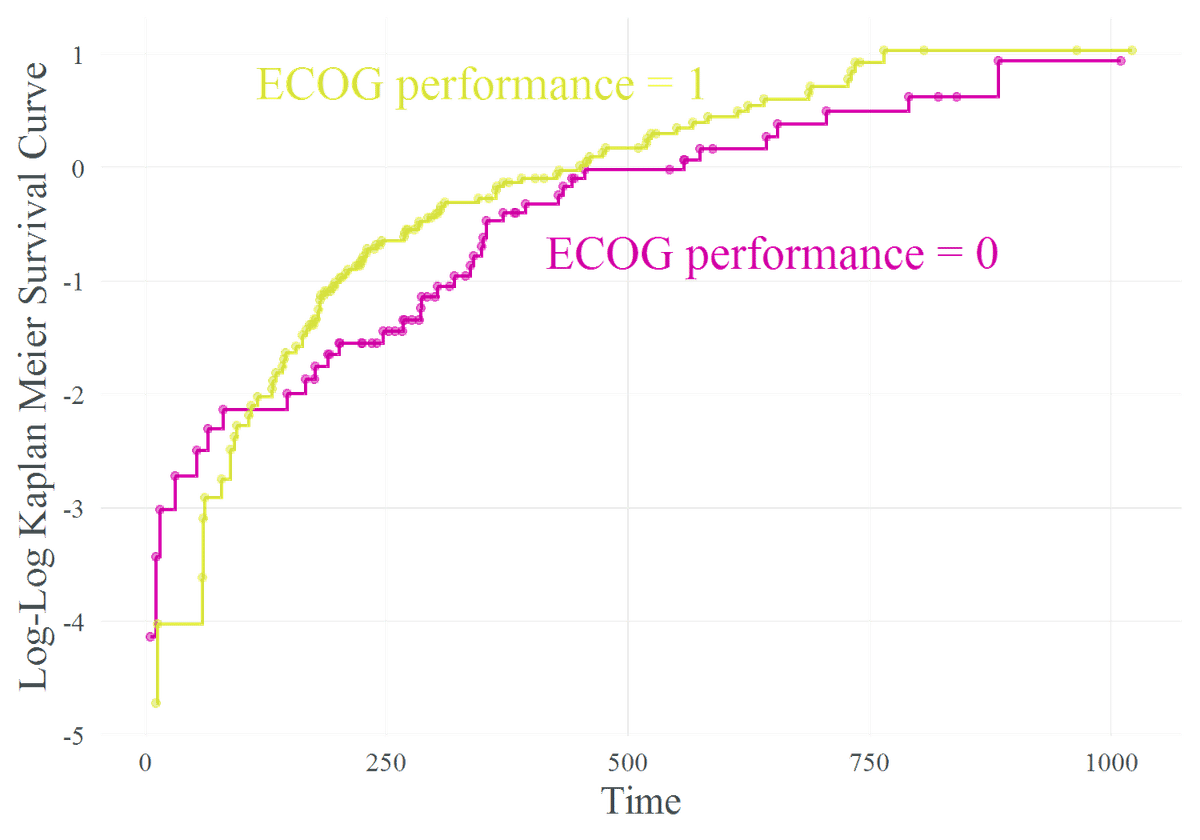

Figure. 2

得られた Figure. 2 をみてみると，Figure. 1 の場合と少し異なり log-log 生存曲線が time = 100 付近で交差しています．
ECOG performance の 0 と 1 をとる変数を共変量とした場合，比例ハザード仮定が成立していなさそうであることを示唆しています．

今回はデータ加工の段階で除いてしまいましたが，本来の ECOG performance は 0 - 4 の値をとりますので，複数分の log-log 生存曲線が平行でないと比例ハザード仮定が成立しないことになります．
しかし，0 と 1 の群を使い描画した時点で，比例ハザード仮定の成立は既に難しそうであることがわかりました．

---

ここまでは，「二つの群のみをもつ共変量を使った Cox-PH モデルにおける比例ハザードの検証」という単純な場合だけを扱ってきたわけですが，実際は次のようなケースが考えられます．

•  連続変数を共変量とする場合
  

•  複数の変数を共変量とする場合

連続変数を共変量とする場合は，適切な binning を行いカテゴリ化してあげる必要があります．ですがこの場合，bin のきり方で KM 曲線の見え方が変わってきてしまうという問題があります．
更に，bin を細かくしカテゴリ数を多くしすぎてしまうと，グラフ上にたくさんの log-log 生存曲線が入り乱れ，何がなんだかわからなくなってしまいそうです．加えて，一つの bin に該当する標本数も少なくなってしまい，果たして得られた log-log 生存曲線は信頼できるものなのだろうか（KM 曲線の信頼区間），という問題もでてきます．
どのような binning が適切かという問いには諸説あるようですが（分位点を使うなど），あくまでも比例ハザードが成立しないことをいうことはできても，比例ハザードが成立することを保証できるものではないと考えておいた方が無難かもしれません．
以上のような欠点があるため，冒頭で述べた通り，グラフを使った方法はあくまでも事前調査的な方法である点を念頭にいれておきましょう．

複数の変数を共変量とする場合は，全共変量がカテゴリ変数だったとしても少し困ったことになります．
例えば，変数 A が 2 群，変数 B が 3 群あった場合，それらの組み合わせは全部で 6 種類になってしまいます．こうなると，上で述べた bin を細かくしカテゴリ数が多くなってしまった場合と変わらない問題が発生してしまいます．
一応ですが，対応策がないわけではありません．
その一つとして，
（i）比例ハザード仮定が満たされていると考えられる他の共変量で調整した上で，（ii）比例ハザード仮定の検証をしたい共変量について log-log 生存曲線を描きプロット間の平行性を検証する
という方法が知られています．
ですが，共変量で調整する作業などを考えると，次回以降で解説する「適合度による方法」や「共変量を使う方法」を採用する方が良いかもしれません．

---

さて，今回はここで終わりにしたいと思います．
次回以降は定性的な比例ハザード仮定の検証手法ではなく，定量的な手法をみていきたいと思います．研究論文などで採用されているのは定量的な手法ですので，丁寧に理解していきたいところです．

それではまた次回！

4. Codes

5. Reference

エモリー大学クラインバウム教授の生存時間解析

Rによるデータサイエンス(第2版):データ解析の基礎から最新手法まで