松廼屋|論点解説 薬剤師国家試験対策ノート問107-178【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数
第107回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問107-178
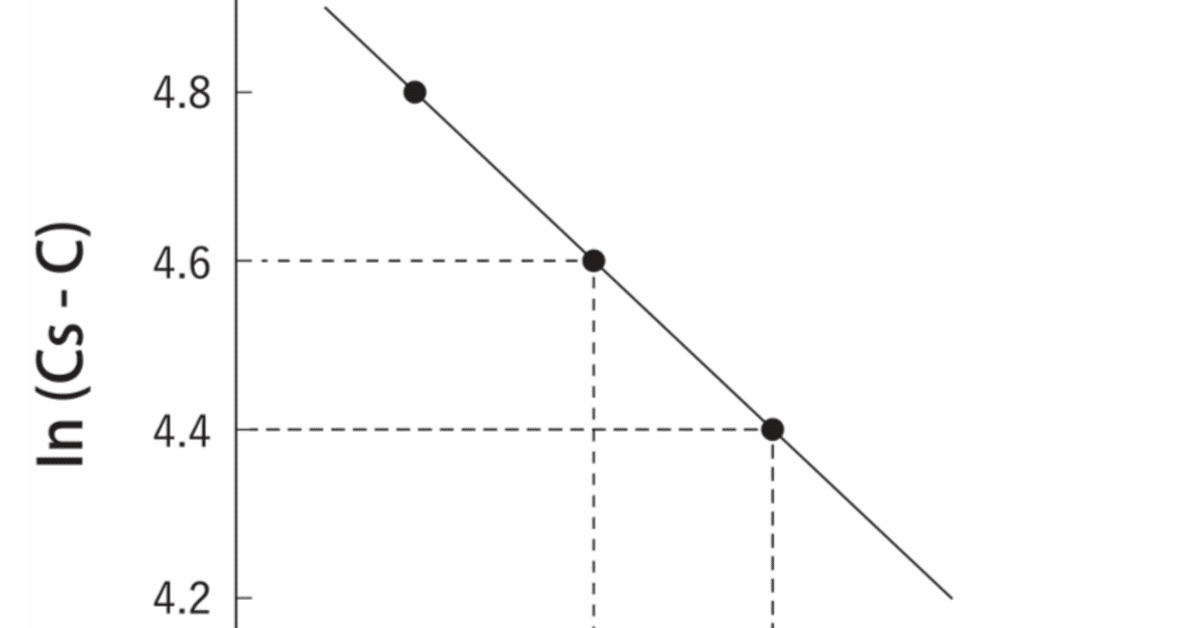
Q. 固体薬物の溶解速度を回転円盤法を用いて温度一定の条件で測定したところ、図のような結果となった。試験液中の薬物濃度(C)が薬物の溶解度(Cs)の半分に達するまでの時間(min)に最も近いのはどれか。1つ選べ。ただし、実験開始時の試験液中の薬物濃度は0、円盤の有効表面積(1cm^2)は試験中に変化せず、溶解はシンク条件において拡散律速で進行するものとする。なお、ln2=0.69とする。

■選択肢
1. 3.5
2. 7
3. 10.5
4. 14
5. 17.5
こんにちは!薬学生の皆さん。
Mats & BLNtです。
matsunoya_note から、薬剤師国家試験の論点解説をお届けします。
苦手意識がある人も、この機会に、薬学理論問題【薬剤】を一緒に完全攻略しよう!
今回は、第107回薬剤師国家試験|薬学理論問題 / 問178、論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数を徹底解説します。
薬剤師国家試験対策ノート NOTE ver.
matsunoya_note|note https://note.com/matsunoya_note
Here; https://note.com/matsunoya_note/n/ne1a0742ffc8c
松廼屋|論点解説 薬剤師国家試験対策ノート問107-178【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数
薬剤師国家試験対策には、松廼屋の eラーニング
「薬剤師国家試験対策ノート」
マガジン|薬剤師国家試験対策ノート on note
👉マガジンをお気に入りに登録しよう!
このコンテンツの制作者|
滝沢 幸穂 Yukiho Takizawa, PhD
https://www.facebook.com/Yukiho.Takizawa
お友達や知り合いに、matsunota_note で学習したeラーニングを勧めてみたい方は、いいね!、口コミ、おススメなど、よろしくお願いします!
設問へのアプローチ|

第107回薬剤師国家試験の問178(問107-178)では、溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数に関する知識を問われました。

計算問題は、慣れです。
手を動かして繰り返し解いてみてください。
2分30秒以内に解けるか、タイマーで時間を測定しながら解いてみると自信がつきます。
グラフから数字を読み取ってから計算に入る問題の場合、最初に必要な数字はメモっておくと計算がしやすいです。
時間(min)|ln(Cs – C)
4|4.6
6|4.4

また、論点整理を読んで、計算工程を覚えるのもポイントです。
今回は、傾き-kAを求める工程と切片ln(Cs)を求める工程があります。
Nernst-Brunner方程式 / Noyes-Whitney方程式を暗記していないと解けない問題ですが、暗記していれば、Y = aX + b の a と b を求める問題です。
正確には、今回の場合、ゴールが薬物濃度(C)が薬物の溶解度(Cs)の半分に達するまでの時間(min)を求めることなので、切片は計算工程で消えるため、計算する必要はないです。時間の無駄です。
薬物濃度(C)が薬物の溶解度(Cs)の半分に達するまでの時間(min)を求める式
C = Cs / 2
Cs - C = Cs / 2
よって
ln(Cs / 2) = ln(Cs) - ln(2) = -kAt + ln(Cs)
ここで、A = 1
よって
t = ln(2) / k
= 0.69 / k
k = 0.2/2 = 0.1
よって、
t = 0.69 / 0.1 ≒ 7 min
この問題に限っては、計算の工程を丸暗記したほうが早いです。
何度か解いてみてください。
溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数は、第109回薬剤師国家試験の問180(問109-180)でも取り上げたテーマです。
第109回薬剤師国家試験の問180(問109-180)にもチャレンジしてみてください。論点解説はこちらです。👇
松廼屋|論点解説 薬剤師国家試験対策ノート問109-180【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数|matsunoya
出題範囲:
製剤化のサイエンス|製剤の性質|固形材料|
粉体の性質について説明できる。
結晶(安定形及び準安定形)や非晶質、無水物や水和物の性質について説明できる。
固形材料の溶解現象(溶解度、溶解平衡等)や溶解した物質の拡散と溶解速度について説明できる。👈ココ
固形材料の溶解に影響を及ぼす因子(pHや温度等)について説明できる。
固形材料の溶解度や溶解速度を高める代表的な製剤的手法を列挙し、説明できる。
薬剤師国家試験 出題基準
出典: 薬剤師国家試験のページ |厚生労働省 (mhlw.go.jp)
出題基準 000573951.pdf (mhlw.go.jp)
今回の解説は、溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数を語らせたら、ちょっと間違っちゃったり💦、ややまわりくどかったりする Grok 2 mini (beta) と、Nernst-Brunner方程式は記憶にほとんどない状態なので、頼りないながら Grok 2 mini (beta) と対話して、細かい校正を加えたワタシのコラボです(^^)/
Grok 2 mini (beta) がビュンビュン系ではなくなってきた。😭
(生成AIプラットフォーマーの開発方針によれば、よくある、アルジャーノン🐭に花束💐をささげたくなる🙏残念な仕上がりですけれど…😎)
でも、基本の型を覚えるのは大事なので、時間があったらじっくり考えながら最後まで読んでください。

基本的な知識について復習しておきましょう。
■■Grok 2 mini (beta)
固体薬物の溶解速度が拡散律速である場合の解析の式は、一般的にNoyes-Whitney方程式またはNernst-Brunner方程式として知られています。
これらの方程式は、溶解速度が溶質と溶媒間の界面での拡散に律速される場合の溶解速度を表現します。
具体的には、以下のような微分方程式の形式を取ります:

Nernst-Brunner方程式
dC / dt = D ・ A / h ・ (Cs - C)
ここで、
dC / dt は溶解速度、
D は溶質の拡散係数、
A は溶解する固体の表面積、
h は溶出層の厚さ、
Cs は溶解度、
C は時間 t における溶液中の濃度です。
この方程式を積分して、時間に対する濃度の変化を表す式を得ることができます。
Noyes-Whitney方程式またはNernst-Brunner方程式を積分して、時間に対する溶解速度を表現するプロセス
初期条件
まず、初期条件を設定します。溶解が始まるとき(t=0)、溶液中の濃度 C は0とします。
C(0) = 0
方程式の設定
Noyes-Whitney方程式は以下のように表されます:
dC / dt = k ・ (Cs - C)
ここで、 k は溶解速度定数で、 k = D ・ A / V ・ h です。 V は溶液の体積で、ここでは単一の溶解体積を考慮するために無視することができます。
積分の準備
この微分方程式を解くためには、両辺を (Cs - C) で割って変形し、部分積分の形に持ち込みます。
dC / (Cs - C) = k ・ dt
積分
両辺を積分します。左辺は C に関する積分、右辺は t に関する積分です。

∫ dC / (Cs - C) = ∫ k ・ dt
左辺の積分は次のように行います:
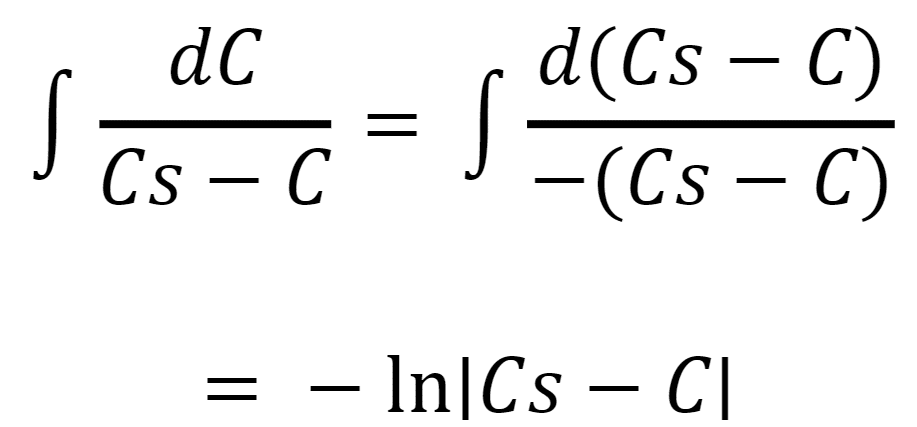
∫ dC / (Cs - C) = ∫ d(Cs - C) / -(Cs - C) = -ln|Cs - C|
右辺は簡単に積分できます:

∫ k ・ dt = k ・ t
定数と初期条件の適用
積分定数を I とし、初期条件 C(0) = 0 を適用します。
-ln|Cs - C| = kt + I
初期条件を代入すると:
-ln|Cs - 0| = k ・ 0 + I
-ln(Cs) = I
最終的な式
これを元の積分結果に含めると:
-ln|Cs - C| = kt - ln(Cs)
対数を解消するために、両辺を指数関数で表します:
ln(Cs) - ln(Cs - C) = kt
ln(Cs / Cs - C) = kt
Cs / (Cs – C) = e^kt
最終解
最後に C の式を求めます:
Cs = (Cs - C) ・ e^kt
Cs ・ e^-kt = Cs - C
C = Cs(1 - e^(-kt))
これが、時間 t における溶解物質の濃度 C を表す最終的な解です。ここで、 Cs は溶解度、 k は溶解速度定数です。この式は、溶解速度が拡散律速である場合の固体薬物の溶解速度の時間依存性を示しています。
Noyes-Whitney方程式とNernst-Brunner方程式の違い
Noyes-Whitney方程式
この方程式は、A.A. NoyesとW.R. Whitneyによって1897年に提唱されました。基本的な形は以下の通りです:

dC / dt = k ・ A ・ (Cs - C)
ここで、
dC / dt は溶解速度(時間当たりの濃度変化率)
k は溶解速度定数
A は溶解する固体の表面積
Cs は溶解度(溶液が飽和する濃度)
C は溶液中のある時点での濃度
Nernst-Brunner方程式
この方程式は、W. NernstとS. Brunnerによって1904年に提案されました。Noyes-Whitney方程式を基にさらに発展させ、拡散係数や溶解層の厚さを明示的に含めた形です:

dC / dt = D ・ A / h ・ (Cs - C)
ここで、
D は溶質の拡散係数
h は溶解層の厚さ(溶質が溶ける際の液体層の厚み)
その他の変数はNoyes-Whitney方程式と同じ
主な違い
物理的なパラメータの明示:
Nernst-Brunner方程式は拡散係数 D と溶解層の厚さ h を明示的に含んでいます。これにより、溶解速度が拡散プロセスにどのように依存するかをより詳細に記述します。
Noyes-Whitney方程式は k を一つの定数として扱い、内部的にこれらの物理パラメータを含んでいますが、明示的には示されません。
理論的背景:
Nernst-Brunner方程式は、溶解速度が溶解層での拡散に律速されるという理論的な背景をより直接的に反映しています。
Noyes-Whitney方程式は、より実験的な観点から導出され、溶解速度を単純化した形で表現します。
応用範囲:
Nernst-Brunner方程式は、溶解プロセスの詳細な解析や、溶解速度を改善する際の理論的な基盤として広く使用されます。
Noyes-Whitney方程式は、溶解速度の基本的な理解や、溶解速度定数 k の実験的決定に重点を置いた応用に適しています。
まとめ
どちらの方程式も固体物質の溶解速度を記述するために有用ですが、Nernst-Brunner方程式は溶解プロセスの物理的な理解を深めるために詳細なパラメータを含んでいる一方で、Noyes-Whitney方程式はその実験的適用性と単純さで好まれます。どちらを使用するかは、研究の目的や必要な精度に依存します。
論点を整理します。
■■Grok 2 mini (beta)
総合的な論点
この問題は、溶解速度論に基づくものであり、特に固体薬物の溶解速度が拡散律速である場合の解析を扱っています。
1: 溶解速度定数 k の求め方
まず、与えられたデータから溶解速度定数 k を求めます。溶解速度が拡散律速の場合、溶解速度式は以下のようになります:

dC / dt = k ・ A ・ (Cs - C)
ここで、C は時間 t での薬物濃度、Cs は溶解度、A は有効表面積、k は溶解速度定数です。
積分すると:

ln(Cs - C) = -k ・ A ・ t + ln(Cs)
この式に与えられたデータを適用して k を求めます。
2: 直線の傾きから k を計算

与えられたデータ:
4分時:ln(Cs - C) = 4.6
6分時:ln(Cs - C) = 4.4
これらの点を使って直線の傾きを求めます:
傾き = Δ ln(Cs - C) /Δ t = (4.4 - 4.6) / (6 – 4) = -0.2 / 2 = -0.1
傾き m = -k ・ A より、
-0.1 = -k ・ 1 ⇒ k = 0.1 min^-1
3: 溶解度 ln(Cs) を求める
t = 4 分のデータを式に代入:
4.6 = -0.1 ・ 4 + ln(Cs)
4.6 = -0.4 + ln(Cs)
ln(Cs) = 5
4: 薬物濃度が溶解度の半分に達する時間を求める
目的の濃度は Cs/2 です。すなわち Cs - C = Cs/2 となる時です。
ln(Cs / 2) = ln(Cs) - ln(2)
ln(Cs / 2) = 5 - 0.69 = 4.31
これを溶解速度の式に代入:
4.31 = -0.1 ・ t + 5
-0.69 = -0.1t
t = 0.69 / 0.1 = 7 分
結論
薬物濃度が溶解度の半分に達するまでにかかる時間は 7分 です。
Ref.
Noyes, A. A., & Whitney, W. R. (1897). "The rate of solution of solid substances in their own solutions." Journal of the American Chemical Society, 19(12), 930-934.
Sinko, P. J. (2006). Martin's Physical Pharmacy and Pharmaceutical Sciences. Lippincott Williams & Wilkins.
Brunner, E., & Tolloczko, S. (1900). "Über die Auflösungsgeschwindigkeit fester Körper." Zeitschrift für Physikalische Chemie, 35(1), 283-290.
以上で、論点整理を終わります。
理解できたでしょうか?
大丈夫です。
完全攻略を目指せ!
はじめましょう。
薬剤師国家試験の薬学理論問題【薬剤】から溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数を論点とした問題です。
なお、以下の解説は、著者(Yukiho Takizawa, PhD)がプロンプトを作成して、その対話に応答する形でGPT4o & Copilot 、Gemini 1.5 Pro、またはGrok 2 (beta) が出力した文章であって、著者がすべての出力を校閲しています。
生成AIの製造元がはっきりと宣言しているように、生成AIは、その自然言語能力および取得している情報の現在の限界やプラットフォーム上のインターフェースのレイト制限などに起因して、間違った文章を作成してしまう場合があります。
疑問点に関しては、必要に応じて、ご自身でご確認をするようにしてください。
松廼屋|論点解説 薬剤師国家試験対策ノート問107-178【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数|matsunoya (note.com)
Here we go.
第107回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問107-178
Q. 固体薬物の溶解速度を回転円盤法を用いて温度一定の条件で測定したところ、図のような結果となった。試験液中の薬物濃度(C)が薬物の溶解度(Cs)の半分に達するまでの時間(min)に最も近いのはどれか。1つ選べ。ただし、実験開始時の試験液中の薬物濃度は0、円盤の有効表面積(1cm^2)は試験中に変化せず、溶解はシンク条件において拡散律速で進行するものとする。なお、ln2=0.69とする。

■選択肢
1. 3.5
2. 7
3. 10.5
4. 14
5. 17.5
■■Grok 2 mini (beta)
薬剤|問 107-178
■論点|溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数
この問題の論点は、固体薬物の溶解速度が拡散律速である場合の解析を通じて、溶解度の半分に達する時間を特定することです。
ln(Cs - C) = -k ・ A ・ t + ln(Cs)
■解説1|
この問題の解決には、溶解速度定数 k を求め、その後溶解度の半分に達する時間 t を計算するプロセスが必要です。
データから直線の傾きを導き、溶解速度定数を求め、溶解度 Cs の半分に達するまでの時間を公式に代入します。
データから直線の傾きを求める: 与えられたデータから傾きを算出。
溶解速度定数 k を求める: 傾きから k を計算。
溶解度 ln(Cs) の算出: 傾きから切片 ln(Cs) を決定。(※今回は不要)
目的の時間 t を求める: 溶解度の半分に達するまでの時間を計算。
■解説2|

データから直線の傾きを求める:
4分と6分の時点での ln(Cs - C) を用いて直線の傾きを求めます。
時間(min)|ln(Cs – C)
4|4.6
6|4.4
傾き m =Δ ln(Cs - C) /Δ t = (4.4 - 4.6) / (6 - 4) = -0.1 。溶解速度定数 k を求める:
傾き m = -k ・ A より k = -m = 0.1 となります。溶解度 ln(Cs) の算出:
4分のデータに傾きを代入します。
4.6 = -0.1 ・ 4 + ln(Cs)
4.6 = -0.4 + ln(Cs)
ln(Cs) = 5目的の時間 t を求める:
ln(Cs / 2) = ln(Cs) - ln(2)
ln(Cs / 2) = 5 - 0.69 = 4.31
これを溶解速度の式に代入します。
4.31 = -0.1 ・ t + 5
-0.69 = -0.1t
t = 0.69 / 0.1 = 7 分。
■結論|
薬物の濃度が溶解度の半分に達するまでの時間は 7分 です。
💡少し早い解き方
C = Cs / 2
Cs - C = Cs / 2
よって
ln(Cs / 2) = ln(Cs) - ln(2) = -kAt + ln(Cs)
ここで、A = 1
よって
t = ln(2) / k
= 0.69 / k
k = 0.2/2 = 0.1
よって、
t = 0.69 / 0.1 ≒ 7 min
■補足|
溶解速度論の基本式:
拡散律速の溶解速度は dC / dt = k ・ (Cs - C) であり、この式に基づいて解析を行いました。直線の傾きと溶解速度定数:
直線の傾きが溶解速度定数 k に対する直接的な指標となるのは、溶解がシンク条件下で拡散律速であるという仮定に基づきます。

必須問題の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 必須問題 第106回-第109回 一覧 powered by Gemini 1.5 Pro, Google AI Studio & GPT4, Copilot|matsunoya (note.com)
薬学理論問題【薬剤】(1) の解説はこちらからどうぞ。
薬剤師国家試験対策ノート|論点解説 薬学理論問題 薬剤(1) 第106回-第109回 31問 powered by GPT4o, Chat GPT|matsunoya (note.com)
お疲れ様でした。
🍰☕🍊
では、問題を解いてみましょう!
すっきり、はっきりわかったら、合格です。
第107回薬剤師国家試験|薬学理論問題 /
問178
一般問題(薬学理論問題)【薬剤】
問107-178
Q. 固体薬物の溶解速度を回転円盤法を用いて温度一定の条件で測定したところ、図のような結果となった。試験液中の薬物濃度(C)が薬物の溶解度(Cs)の半分に達するまでの時間(min)に最も近いのはどれか。1つ選べ。ただし、実験開始時の試験液中の薬物濃度は0、円盤の有効表面積(1cm^2)は試験中に変化せず、溶解はシンク条件において拡散律速で進行するものとする。なお、ln2=0.69とする。

■選択肢
1. 3.5
2. 7
3. 10.5
4. 14
5. 17.5
楽しく!驚くほど効率的に。
https://note.com/matsunoya_note
お疲れ様でした。
🍰☕🍊
またのご利用をお待ちしております。
ご意見ご感想などお寄せくださると励みになりうれしいです。
note からのサポート、感謝します。
今日はこの辺で、
それではまた
お会いしましょう。
Your best friend
Mats & BLNt
このコンテンツ
松廼屋|論点解説 薬剤師国家試験対策ノート問107-178【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数|matsunoya (note.com)
Here; https://note.com/matsunoya_note/n/ne1a0742ffc8c
よろしければこちらもどうぞ
このコンテンツの制作者|
滝沢幸穂(Yukiho.Takizawa)phD
■Facebook プロフィール
https://www.facebook.com/Yukiho.Takizawa
■X (Former Twitter) プロフィール 🔒
https://twitter.com/YukihoTakizawa
CONTACT|
mail: info_01.matsunoya@vesta.ocn.ne.jp (Matsunoya Client Support)
tel: 029-872-9676
日々の更新情報など、Twitter @Mats_blnt_pharm から発信しています!
🔒 🐤💕 https://twitter.com/Mats_blnt_pharm
https://note.com/matsunoya_note
note.com 右上の🔍で
( matsunoya_note 🔍 )
松廼屋 Mats.theBASE
https://matsunoya.thebase.in/
サポート感謝します👍
最後までお読みいただきましてありがとうございました。
Here; https://note.com/matsunoya_note/n/ne1a0742ffc8c
松廼屋|論点解説 薬剤師国家試験対策ノート問107-178【薬剤】論点:溶解度 / Nernst-Brunner方程式 / Noyes-Whitney方程式 / 溶解速度定数|matsunoya (note.com)
ここから先は
¥ 700
医療、健康分野のリカレント教育における「最強コンテンツ」を note で誰でもいつでも学習できる、 https://note.com/matsunoya_note はそんな場にしたい。あなたのサポートがあれば、それは可能です。サポート感謝します!松廼屋 matsunoya
